Task02: linked list

1. Video title

1.1 Remove linked list elements

1.1.1 describe

Give you a list of the head node head And an integer val , Please delete all the contents in the linked list Node.val == val The node of , And back to New head node .

Example 1：

Input ：head = [1,2,6,3,4,5,6], val = 6
Output ：[1,2,3,4,5]

Example 2：

Input ：head = [], val = 1
Output ：[]

Example 3：

Input ：head = [7,7,7,7], val = 7
Output ：[]

Tips ：

The number of nodes in the list is in the range [0, 104] Inside
1 <= Node.val <= 50
0 <= val <= 50

1.1.2 Code

The given linked list is actually a linked list without head nodes , Because the value of the first node is meaningful

So for ease of operation , Here we redefine a header node , Its value is empty

This new header node is mainly used to determine whether the original header node needs to be removed

# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
    def removeElements(self, head: ListNode, val: int) -> ListNode:
        new_head = ListNode()
        new_head.next = head
        prev = new_head
        while prev.next :
            if prev.next.val == val:
                prev.next = prev.next.next
            else:
                prev = prev.next
        return new_head.next

1.1.3 summary

We have created a new header node , In addition to the convenience of judging the original head node

The criteria of the cycle are also determined , namely prev.next, It is convenient to remove elements after they are found

So if you want to remove elements , It's generally used .next.val Judge

Find it this way val after , Skip the element directly , namely .next = .next.next

1.2 Rotate the list

1.2.1 describe

Give you a list of the head node head , Rotate the list , Move each node of the list to the right k A place .

Example 1：

Input ：head = [1,2,3,4,5], k = 2
Output ：[4,5,1,2,3]

Example 2：

Input ：head = [0,1,2], k = 4
Output ：[2,0,1]

Tips ：

The number of nodes in the linked list is in the range [0, 500] Inside
-100 <= Node.val <= 100
0 <= k <= 2 * 109

1.2.2 Code

Rotate the list , That is to say, you need to connect the linked list end to end to form a ring , Then disconnect at the new tail node

Because each node is moved to the right k A place , So go from the end k The element reached by step is the new tail node

But the linked list is one-way , So we have to count from the beginning , That is, from the new head node length-k The node reached by step

Here's a detail , Suppose the length of the linked list is length, Then there are between the first and last nodes length-1 An interval , That's the step length

So if you start from the head node of the original linked list , It needs to be moved (length-1) - k A step

among ,length-1 Is the interval between the beginning and the end ,k Is the step size between the new tail node and the old tail node , That is to move to the right k A place

Because we have newly set an empty header node for the convenience of operation , step +1, So you need to move to the right length-k A step

# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
    def rotateRight(self, head, k):
        
        dummy = ListNode(0)
        #  Create a new header node for easy operation 
        dummy.next = head
        #  Connect the head node of the original linked list 
        if head is None:
            return None
        #  If the linked list is empty, it will be returned directly 
        i = head
        #  Start from the head node of the original linked list 
        length = 1
        #  Start counting 
        while i.next is not None:
            i = i.next
            length += 1
        #  Traversal access , Get the interval length and tail node 
        k = k%length
        #  Linked lists form rings , It is possible to move more than one turn to the right 
        if (k == 0) or length == 1:
            return head
        #  If it just moves right length position , That is unchanging 
        #  Or the linked list has only one element , That is the same 
        
        i.next = head
        #  end to end , Linked lists form rings 
 
        i = dummy
        for _ in range(length - k):
            i = i.next
        #  Start with the new empty header node 
        #  To the right length-k Step 
        #  Find the location of the new tail node 
        
        j = i.next
        #  New head node 
        
        i.next = None
        #  New tail node 
        
        return j
        #  Return to header node 

1.2.3 summary

The first is the judgment of special circumstances , One is that the moving step length is exactly equal to the interval length of the linked list

It's just a circle , Back to the original position , That is, there is no change

Another is that there is only one element , No matter how it moves, it remains unchanged

And then after the ring is formed , Pay attention to the surplus , That is, to deal with the situation of moving more than one circle

Finally, the length of the main interval is different from that of the linked list , The difference between the two is 1 position

2. Assignment topic

2.1 Merge two ordered lists

2.1.1 describe

Merge two ascending linked lists into a new Ascending Link list and return . The new linked list is made up of all the nodes of the given two linked lists .

Example 1：

Input ：l1 = [1,2,4], l2 = [1,3,4]
Output ：[1,1,2,3,4,4]

Example 2：

Input ：l1 = [], l2 = []
Output ：[]

Example 3：

Input ：l1 = [], l2 = [0]
Output ：[0]

Tips ：

The range of the number of nodes in the two linked lists is [0, 50]
-100 <= Node.val <= 100
l1 and l2 All according to Non decreasing order array

2.1.2 Code

The most intuitive idea is to compare the head nodes of two old linked lists in turn , Then add the small ones to the new linked list

Note that the two old linked lists are empty , Or if the values of the two old chain header nodes are equal

So we used it directly in both cases else To judge

# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
    def mergeTwoLists(self, l1: ListNode, l2: ListNode) -> ListNode:
        head = ListNode(0)
        temp = head
        while l1 and l2:
            if l1.val < l2.val :
               temp.next = l1
               l1 = l1.next
               temp = temp.next
            else:
                temp.next = l2
                l2 = l2.next
                temp = temp.next
        if l1:
            temp.next = l1
        else:
            temp.next = l2
        
        return head.next
        

There is also a recursive solution , Running time is even longer , And the idea doesn't seem intuitive

But if we think recursively , It may be more intuitive to find this way

It seems to have a little meaning of dynamic planning , Superposition optimal sub solution , To achieve the optimal solution

It only compares the size of the current value , By default, the following values are the ordered optimal substructures

Then recursively call itself to ensure that the following values are ordered

# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
    def mergeTwoLists(self, l1: ListNode, l2: ListNode) -> ListNode:
        if l1 is None:
            return l2
        elif l2 is None:
            return l1
        elif l1.val < l2.val:
            l1.next = self.mergeTwoLists(l1.next, l2)
            return l1
        else:
            l2.next = self.mergeTwoLists(l1, l2.next)
            return l2

2.1.3 summary

If the values are equal , Both operations can be handled , That is suitable for use else, direct charging else Category

2.2 Intersecting list

2.2.1 describe

Here are two head nodes of the single linked list headA and headB , Please find out and return the starting node where two single linked lists intersect . If two linked lists do not have intersecting nodes , return null .

Figure two linked lists at the node c1 Start meeting ：

Subject data Guarantee There is no ring in the whole chain structure .

Be careful , Function returns the result , Linked list must Keep its original structure .

Custom profiling ：

Evaluation system The input is as follows （ The program you designed Do not apply This input ）：

intersectVal - The value of the starting node of the intersection . If there are no intersecting nodes , This value is 0
listA - The first list
listB - The second list
skipA - stay listA in （ Start from the beginning ） Number of nodes jumping to cross nodes
skipB - stay listB in （ Start from the beginning ） Number of nodes jumping to cross nodes
The evaluation system will create a linked data structure based on these inputs , And the two header nodes headA and headB The program passed to you . If the program returns the intersection node correctly , Then your solution will be Take it as the right answer .

Example 1：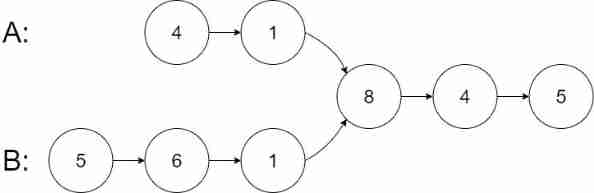

Input ：intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3
Output ：Intersected at ‘8’
explain ： The value of the intersection node is 8 （ Be careful , If two linked lists intersect, they cannot be 0）.
Starting from the respective heads , Linked list A by [4,1,8,4,5], Linked list B by [5,6,1,8,4,5].
stay A in , There is... Before the intersection node 2 Nodes ; stay B in , There is... Before the intersection node 3 Nodes .

Example 2：

Input ：intersectVal = 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
Output ：Intersected at ‘2’
explain ： The value of the intersection node is 2 （ Be careful , If two linked lists intersect, they cannot be 0）.
Starting from the respective heads , Linked list A by [1,9,1,2,4], Linked list B by [3,2,4].
stay A in , There is... Before the intersection node 3 Nodes ; stay B in , There is... Before the intersection node 1 Nodes .

Example 3：

Input ：intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
Output ：null
explain ： Starting from the respective heads , Linked list A by [2,6,4], Linked list B by [1,5].
Because these two linked lists don't intersect , therefore intersectVal It has to be for 0, and skipA and skipB It could be any value .
The two lists don't intersect , Therefore return null .

Tips ：

listA The number of nodes in is m
listB The number of nodes in is n
1 <= m, n <= 3 * 104
1 <= Node.val <= 105
0 <= skipA <= m
0 <= skipB <= n
If listA and listB There is no point of intersection ,intersectVal by 0
If listA and listB There are intersections ,intersectVal==listA[skipA]==listB[skipB]

Advanced ： Can you design a time complexity O(m + n) 、 Just use O(1) Memory solutions ？

2.2.2 Code

The simplest and most intuitive way is to type a watch , First, create a hash table for one of the linked lists

Then traverse another linked list , When encountering the same, it will jump out and return to the intersection node

# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None

class Solution(object):
    def getIntersectionNode(self, headA, headB):
        d = dict()
        while headA:
            d[headA] = 1
            headA = headA.next
        while headB:
            if headB in d:
                return headB
            headB = headB.next
        return None

There is also a double pointer solution , The idea is also magical and ingenious

I think it's for the pointer a, Let him run on the list B Inside the self forming ring , The pointer b On the contrary

After entering the ring , The two pointers move at the same speed , But the length of the two linked lists is different , So meet

If two linked lists have the same length , Then there is no need to enter the ring , Meet directly at the intersection

But if the pointer a and b Each of them runs in A and B Inside their respective rings , Then something goes wrong

Or it is an endless loop in which two linked lists do not intersect , Or running too long and overtime

Maybe that's not intuitive enough , We can flatten the two linked lists , Fixed pointer , Move linked list

Then we can find , When a,b After running their respective lists, they enter each other's rings , Just run the length before the intersection

hypothesis A The length before the intersection is $\alpha$,B The length before the intersection is $\beta$, The length after intersection is $\theta$

Flatten the list , The pointer a ran $\alpha +\theta +\beta$,b ran $\beta +\theta +\alpha$, The two meet

If the two don't intersect , set up A The length of is $\alpha$,B The length of is $\beta$, When they meet, they are None

among a ran $\alpha +\beta$, and b ran $\beta +\alpha$, The same length meets at the end

The above ideas come from blogs ¹, See the explanation and drawings for details

# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None

class Solution(object):
    def getIntersectionNode(self, headA, headB):
        pA = headA
        pB = headB
        while pA != pB :
            pA = pA.next if pA else headB
            pB = pB.next if pB else headA
                
        return pA

2.2.3 summary

If you only ask to pass the title , Of course, long live the clock

From the perspective of moving the pointer in a fixed linked list , To use double pointers , There must be a difference between the two , Otherwise, we cannot meet

The ingenious part of this question is when the length of the two linked lists is the same , The pointer will meet before entering the loop

And if the title itself has no ring , We can construct rings to use double pointers

And we can change the angle of view when forming a ring , That is, the linked list is leveled and connected , Fixed pointer moves linked list

2.3 Delete duplicate elements from the sort list II

2.3.1 describe

Given the header of a sorted linked list head , Delete all nodes with duplicate numbers in the original linked list , Leave only different numbers . return Sorted linked list .

Example 1：

Input ：head = [1,2,3,3,4,4,5]
Output ：[1,2,5]

Example 2：

Input ：head = [1,1,1,2,3]
Output ：[2,3]

Tips ：

The number of nodes in the linked list is in the range [0, 300] Inside
-100 <= Node.val <= 100
The title data ensures that the linked list has been in ascending order array

2.3.2 Code

Completely erase duplicate elements , So you need to record the previous element of the repeating sequence

And connect it to the first element after the repeating sequence , So it's a double pointer

A pointer is responsible for recording the previous element of the repeating sequence

The other is responsible for finding the first element after the repeated sequence

Use here next It is reduced to a pointer

# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
    def deleteDuplicates(self, head: ListNode) -> ListNode:
        if not head:
            return head
        
        dummy = ListNode(0, head)
        #  Create a new header node , Make sure you start from the beginning 

        cur = dummy
        
        while cur.next and cur.next.next:
        #  Loop to the end of the list 
            if cur.next.val == cur.next.next.val:
            #  Once a duplicate value is found 
                x = cur.next.val
                #  Get this duplicate number 
                while cur.next and cur.next.val == x:
                #  Anything equal to this value is erased 
                    cur.next = cur.next.next
            else:
                cur = cur.next
            #  Move to the next node 
        return dummy.next

2.3.3 summary

My initial idea was to set up fast and slow Two pointers , Later, it was found that it could be merged into one

And then there's the repeated numbers , This is a sequence , So we need to use a loop to eliminate

---

1. Leetcode 160： Intersecting list （ Super detailed solution ！！！）︎