当前位置:网站首页>【AtCoder1998】Stamp Rally(整体二分+并查集)
【AtCoder1998】Stamp Rally(整体二分+并查集)
2022-06-11 07:23:00 【CaptainHarryChen】
题意
我们有一个N (3<=N<=10^5)个结点和M(N−1≤M≤10^5)个边的无向图。 结点编号为1到N,边编号为1到M。边i连接结点ai和bi。保证图连通。在这张图上,Q(1≤Q≤10^5)对兄弟正在参加一项名为Stamp Rally的活动。 第i对Stamp Rally如下:
一个兄弟从结点xi开始,另一个从结点yi开始。(1≤xi < yi≤N)
两个兄弟沿着边访问图上的结点,总共访问zi(3≤zi≤N)个结点,包括起始结点。 在这里,即使一个结点被多次访问,只计算一次。
定义得分为它们走过的边的最大编号。 他们的目标是尽量减少这个得分。
找出每对兄弟的最低分数。
题解
以边的编号从小到大加入图中,利用并查集,每加入一条边i,扫描所有询问,如果他们所在联通快大小达到了zi,则这个询问的答案 为i。
但这样是O(MQ) O ( M Q ) 的。
利用整体二分,先加入前面一半[l,mid] [ l , m i d ] 的边,判断哪些询问已经达到条件,则这些询问的答案一定≤mid ≤ m i d ,将其划分到前面一半,然后将并查集复原,递归处理[l,mid] [ l , m i d ] 的询问,和[mid+1,r] [ m i d + 1 , r ] 的询问。
为了使并查集复原,可使用按秩合并。
代码
#include<cstdio>
#include<vector>
#include<algorithm>
using namespace std;
const int MAXN=100005;
int N,M,Q;
struct Edge
{
int u,v;
}E[MAXN];
struct Query
{
int x,y,z;
}q[MAXN];
int id[MAXN],tmp[MAXN],mk[MAXN],ans[MAXN];
int stk[MAXN][2],tp;
int fa[MAXN],siz[MAXN];
int Root(int u)
{
if(fa[u]==0)
return u;
return Root(fa[u]);
}
void Union(int u,int v)
{
int r1=Root(u),r2=Root(v);
if(r1==r2)
return;
if(siz[r1]<siz[r2])
swap(r1,r2);
fa[r2]=r1;
stk[++tp][0]=r2;
stk[tp][1]=r1;
siz[r1]+=siz[r2];
}
void solve(int a,int b,int l,int r)
{
if(a==b)
{
for(int i=l;i<=r;i++)
ans[id[i]]=a;
Union(E[a].u,E[a].v);
return;
}
tp=0;
int mid1=(a+b)/2;
for(int i=a;i<=mid1;i++)
Union(E[i].u,E[i].v);
for(int i=l;i<=r;i++)
{
int r1=Root(q[id[i]].x),r2=Root(q[id[i]].y);
if(r1==r2&&siz[r1]>=q[id[i]].z)
mk[i]=1;
if(r1!=r2&&siz[r1]+siz[r2]>=q[id[i]].z)
mk[i]=1;
}
int it=l-1;
for(int i=l;i<=r;i++)
if(mk[i])
tmp[++it]=id[i];
int mid2=it;
for(int i=l;i<=r;i++)
if(!mk[i])
tmp[++it]=id[i];
for(int i=l;i<=r;i++)
id[i]=tmp[i],mk[i]=0;
while(tp)
{
fa[stk[tp][0]]=0;
siz[stk[tp][1]]-=siz[stk[tp][0]];
tp--;
}
solve(a,mid1,l,mid2);
solve(mid1+1,b,mid2+1,r);
}
int main()
{
scanf("%d%d",&N,&M);
for(int i=1;i<=M;i++)
scanf("%d%d",&E[i].u,&E[i].v);
scanf("%d",&Q);
for(int i=1;i<=Q;i++)
scanf("%d%d%d",&q[i].x,&q[i].y,&q[i].z);
for(int i=1;i<=N;i++)
fa[i]=0,siz[i]=1;
for(int i=1;i<=Q;i++)
id[i]=i;
solve(1,M,1,Q);
for(int i=1;i<=Q;i++)
printf("%d\n",ans[i]);
return 0;
}边栏推荐
- 2022 low voltage electrician operation certificate test question simulation test platform operation
- The gap between the parent box and the child box
- Education expert wangzhongze shared his experience for many years: family education is not a vassal
- What is the difference between gaussdb for redis and redis?
- Djikstra solves the shortest circuit with negative weight
- C language inherits memory management mechanism (unfinished)
- Typora set markdown syntax inline mode
- C language volatile
- [analysis of STL source code] summary note (4): behind the scenes hero allocator
- nosqlzoo刷题-1
猜你喜欢

2022 low voltage electrician test questions and online simulation test

二、用户登录和注册

Aiop introduction

多线程复习总结之解析Volatile关键字
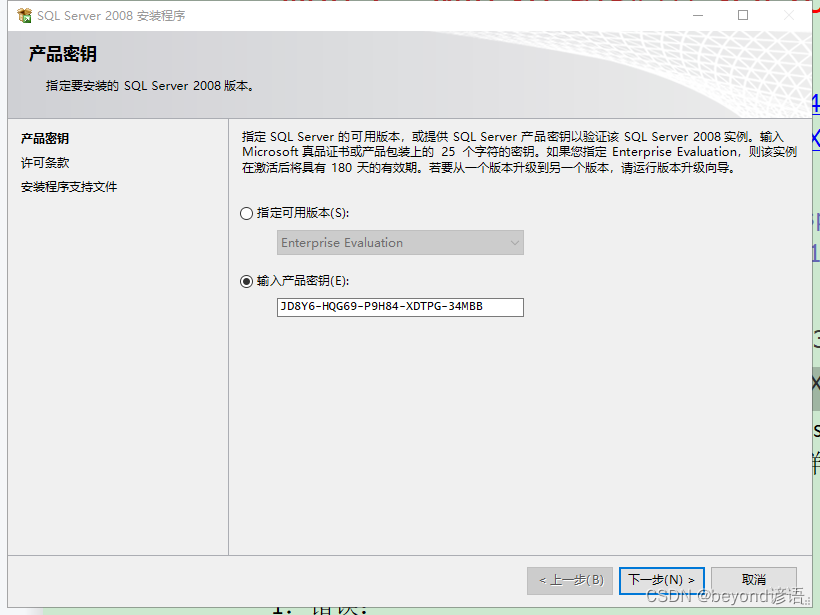
1、 Sqlserver2008 installation (with password), database creation, C form project test

2、 User login and registration

No response from win10 explorer when dragging files

Education expert wangzhongze solves students' problems with one move

一、SQLServer2008安裝(帶密碼)、創建數據庫、C#窗體項目測試

Biological sequence intelligent analysis platform blog (1)
随机推荐
Adventure of small X
20200727 T2 small w playing game [generating function (binomial inversion technique)]
2022低压电工考题及在线模拟考试
正则表达式匹配
Crmeb/v4.4 Standard Version open version mall source code applet official account h5+app mall source code
Several transaction modes of Seata
Leetcode-104. Maximum Depth of Binary Tree
Leetcode-9. Palindrome Numbber
SQLZOO刷题记录-3
2022.5.30-6.5 AI行业周刊(第100期):三年时光
R language Parallel Computing practice tutorial
C language inherits memory management mechanism (unfinished)
Aiop introduction
nosqlzoo刷题-1
Gobang interface of mobile console (C language)
Compound ratemodel contract analysis
big.js--使用/实例
P3172 [cqoi2015] data selection (Mobius inversion + Du Jiao sieve)
Phi and phi (Mobius inversion + formula)
JVM Learning record (7) - - class Loading Process and parent delegation Model