当前位置:网站首页>20200727 T2 small w playing game [generating function (binomial inversion technique)]
20200727 T2 small w playing game [generating function (binomial inversion technique)]
2022-06-11 07:29:00 【Master. Yi】
Title Description


Topic analysis
Equipped with i i i The number of schemes with odd number of times selected in the row is f i f_i fi, j j j The number of schemes selected for odd number of times is g j g_j gj
A n s = ∑ i m + j n − 2 i j ≤ k f i ∗ g j Ans=\sum_{im+jn-2ij\le k} f_i*g_j Ans=∑im+jn−2ij≤kfi∗gj
f i = q ! [ x q ] ( e x − e − x 2 ) i ( e x + e − x 2 ) n − i ( n i ) f_i=q^i(\frac {e^x+e^{-x}}2)^{n-i}\binom ni fi=qi(2ex+e−x)n−i(in)
It's not easy to push directly ( But it is feasible , There's a little trick , I'll talk about it later )
It would be more comfortable if there was only one power . Consider binomial inversion , h i h_i hi To force there to be i i i Row odd , Any other scheme .
h i = q ! [ x q ] ( e x − e − x 2 ) i e ( n − i ) x ( n i ) = ( 1 2 ) i ( n i ) q ! [ x q ] ∑ j = 0 i ( i j ) ( − 1 ) i − j e x ( n − 2 i + 2 j ) h_i=q^ie^{(n-i)x}\binom ni\\ =(\frac 12)^i\binom niq![x^q]\sum_{j=0}^i\binom ij(-1)^{i-j}e^{x(n-2i+2j)} hi=qie(n−i)x(in)=(21)i(in)q![xq]j=0∑i(ji)(−1)i−jex(n−2i+2j)
and q ! [ x q ] e x ( n − 2 i + 2 j ) = ( n − 2 i + 2 j ) q q![x^q]e^{x(n-2i+2j)}=(n-2i+2j)^q q![xq]ex(n−2i+2j)=(n−2i+2j)q
Then we can convolute .
Binomial inversion will be rolled up again .
We're done f , g f,g f,g After enumeration i i i, j ( n − 2 i ) ≤ k − i m j(n-2i)\le k-im j(n−2i)≤k−im, according to n − 2 i n-2i n−2i You can find the corresponding prefix sum by the positive and negative of .
Note that rounding under negative division is larger .
Then I will talk about how to directly deduce the formula without binomial inversion .
For those two very similar bases , Express one in the form of another , namely :
q ! [ x q ] ( n i ) ( 1 2 ) n ( e x − e − x ) i ( e x + e − x ) n − i = q ! [ x q ] ( n i ) ( 1 2 ) n ( e x + e − x − 2 e − x ) i ( e x + e − x ) n − i = q ! [ x q ] ( n i ) ( 1 2 ) n ∑ j = 0 i ( − 2 ) i − j ( e x + e − x ) n − i + j e − x ( i − j ) = q ! [ x q ] ( n i ) ( 1 2 ) n ∑ j = 0 i ( − 2 ) i − j ∑ k = 0 n − i + j ( n − i + j k ) e ( 2 k − n ) x = ( n i ) ( 1 2 ) n ∑ j = 0 i ( − 2 ) i − j ∑ k = 0 n − i + j ( n − i + j k ) ( 2 k − n ) q q![x^q]\binom ni(\frac 12)^n(e^x-e^{-x})^i(e^x+e^{-x})^{n-i}\\ =q![x^q]\binom ni(\frac 12)^n(e^x+e^{-x}-2e^{-x})^i(e^x+e^{-x})^{n-i}\\ =q![x^q]\binom ni(\frac 12)^n\sum_{j=0}^i(-2)^{i-j}(e^x+e^{-x})^{n-i+j}e^{-x(i-j)}\\ =q![x^q]\binom ni(\frac 12)^n\sum_{j=0}^i(-2)^{i-j}\sum_{k=0}^{n-i+j}\binom {n-i+j}ke^{(2k-n)x}\\ =\binom ni(\frac 12)^n\sum_{j=0}^i(-2)^{i-j}\sum_{k=0}^{n-i+j}\binom {n-i+j}k(2k-n)^q q(21)n(ex−e−x)i(ex+e−x)n−i=q(21)n(ex+e−x−2e−x)i(ex+e−x)n−i=q(21)nj=0∑i(−2)i−j(ex+e−x)n−i+je−x(i−j)=q(21)nj=0∑i(−2)i−jk=0∑n−i+j(kn−i+j)e(2k−n)x=(in)(21)nj=0∑i(−2)i−jk=0∑n−i+j(kn−i+j)(2k−n)q
the second ∑ \sum ∑ Can be seen as G ( i − j ) G(i-j) G(i−j), One convolution can find G G G, Then we can roll it again and find out f f f 了 .
Code( Binomial inversion ):
#include<bits/stdc++.h>
#define maxn 550005
using namespace std;
const int mod = 998244353, inv2 = (mod+1)/2;
int w[maxn],r[maxn],WL,fac[maxn],inv[maxn];
int Pow(int a,int b){
int s=1;for(;b;b>>=1,a=1ll*a*a%mod) b&1&&(s=1ll*s*a%mod);return s;}
int C(int n,int m){
return 1ll*fac[n]*inv[m]%mod*inv[n-m]%mod;}
void init(int n){
w[0]=WL=1; while(WL<=n) WL<<=1; w[1]=Pow(3,(mod-1)/WL);
for(int i=2;i<=WL;i++) w[i]=1ll*w[i-1]*w[1]%mod;
fac[0]=fac[1]=inv[0]=inv[1]=1;
for(int i=2;i<=n;i++) fac[i]=1ll*fac[i-1]*i%mod,inv[i]=1ll*(mod-mod/i)*inv[mod%i]%mod;
for(int i=2;i<=n;i++) inv[i]=1ll*inv[i-1]*inv[i]%mod;
}
int upd(int x){
return x+(x>>31&mod);}
void NTT(int *a,int len,int flg){
for(int i=0;i<len;i++) if(i<(r[i]=r[i>>1]>>1|(i&1?len>>1:0))) swap(a[i],a[r[i]]);
for(int i=2,l=1,v;i<=len;l=i,i<<=1)
for(int j=0,t=WL/i;j<len;j+=i)
for(int k=j,o=0;k<j+l;k++,o+=t)
a[k+l]=upd(a[k]-(v=1ll*w[flg^1?WL-o:o]*a[k+l]%mod)),a[k]=upd(a[k]+v-mod);
if(flg^1) for(int i=0,Inv=mod-(mod-1)/len;i<len;i++) a[i]=1ll*a[i]*Inv%mod;
}
int n,m,qq,A[maxn],B[maxn],f[maxn],g[maxn],h[maxn];
long long q,k,lim;
void calc(int n,int *f){
init(2*n);
memset(A,0,sizeof A),memset(B,0,sizeof B);
for(int i=0;i<=n;i++) A[i]=inv[i],B[i]=1ll*(i&1?mod-1:1)*inv[i]%mod*Pow(upd(n-2*i),qq)%mod;
NTT(A,WL,1),NTT(B,WL,1);
for(int i=0;i<WL;i++) A[i]=1ll*A[i]*B[i]%mod;
NTT(A,WL,-1); memset(h,0,sizeof h);
for(int i=0,pw=1;i<=n;i++,pw=1ll*pw*inv[2]%mod) h[i]=1ll*A[i]*fac[n]%mod*inv[n-i]%mod*pw%mod;
memset(A,0,sizeof A),memset(B,0,sizeof B);
for(int i=0;i<=n;i++) A[i]=1ll*h[i]*fac[i]%mod,B[i]=1ll*inv[n-i]*(n-i&1?mod-1:1)%mod;
NTT(A,WL,1),NTT(B,WL,1);
for(int i=0;i<WL;i++) A[i]=1ll*A[i]*B[i]%mod;
NTT(A,WL,-1);
for(int i=0;i<=n;i++) f[i]=1ll*A[n+i]*inv[i]%mod;
}
int main()
{
freopen("b.in","r",stdin);
freopen("b.out","w",stdout);
scanf("%d%d%lld%lld",&n,&m,&q,&k),qq=q%(mod-1);
if(q==0) return puts("1"),0;
calc(n,f),calc(m,g);
for(int i=1;i<=m;i++) g[i]=(g[i]+g[i-1])%mod;
int ans=0;
for(int i=0;i<=n;i++)
if(n>2*i){
if(k>=1ll*i*m) ans=(ans+1ll*f[i]*g[min((k-1ll*i*m)/(n-2*i),1ll*m)])%mod;
}
else if(n<2*i){
if((lim=(1ll*i*m-k+2*i-n-1)/(2*i-n))<=m) ans=(ans+1ll*f[i]*(g[m]-(lim>0?g[lim-1]:0)))%mod;
}
else if(k-1ll*i*m>=0) ans=(ans+1ll*f[i]*g[m])%mod;
printf("%d\n",(ans+mod)%mod);
}
边栏推荐
- 2022年熔化焊接与热切割考试练习题及答案
- [STL source code analysis] summary notes (1): Opening
- Multi thread review summary parsing volatile keyword
- Set center alignment
- What is the lifecycle of automated testing?
- [STL source code analysis] summary note (2): overview of containers
- C language to write a calculator MVC (very interesting code architecture callback and constructor mode and the use of pointer functions)
- MS office level II wrong question record [6]
- Cartland number application
- Configuration software -- control drag and drop
猜你喜欢

webserver

Leetcode-141. Linked List Cycle

Biological sequence intelligent analysis platform blog (1)

If you want to save an IP address, what data type is better? 99% of people will answer wrong!

The rotation of the earth and the moon (II)

Qstring to hexadecimal qstring

Leetcode-104. Maximum Depth of Binary Tree
一、SQLServer2008安装(带密码)、创建数据库、C#窗体项目测试
![[analysis of STL source code] summary notes (6): Design of iterator and magical traits](/img/57/eaf02e880d205c5912f353609c9520.png)
[analysis of STL source code] summary notes (6): Design of iterator and magical traits
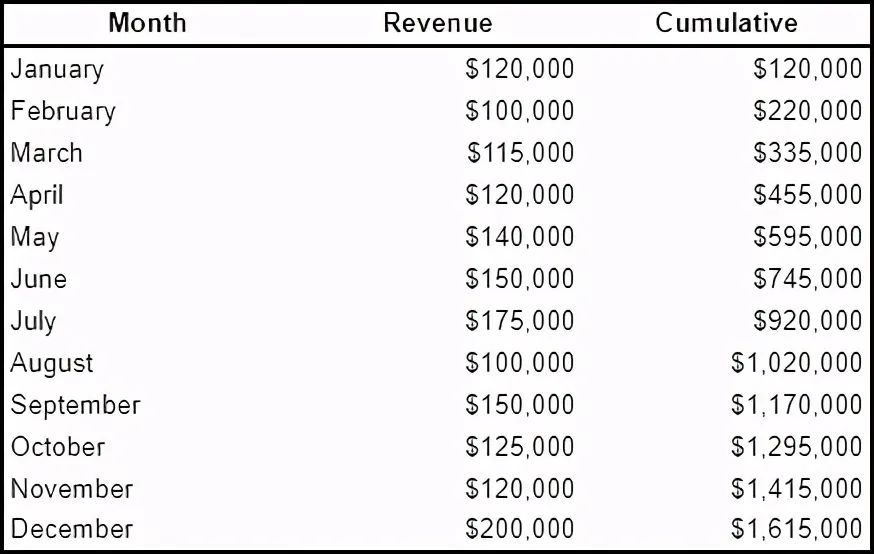
学 SQL 必须了解的10个高级概念
随机推荐
Installation de SQL Server 2008 (avec mot de passe), création d'une base de données, test de projet de formulaire C
Summary of classic interview questions
Outer margin collapse
Arduino_ Esp32 development record
Adventure of small X
【Oracle 数据库】奶妈式教程day04 排序查询
[STL source code analysis] summary notes (5): a good helper for understanding iterators --list
QT 基于QScrollArea的界面嵌套移动
黑群晖DSM7.0.1物理机安装教程
421. maximum XOR value of two numbers in the array
多线程复习总结之解析Volatile关键字
JVM tuning
Biological sequence intelligent analysis platform blog (1)
Pointer to a two-dimensional array
2、 User login and registration
【CF#388 (Div. 2)】A. Bachgold Problem
Mistakes in Niuke JS exercise
MS office level II wrong question record [9]
[Oracle database] mammy tutorial day02 use of database management tool sqlplus
【CodeForces1019E】Raining season(边分治+斜率优化)