当前位置:网站首页>Polygon zkEVM 基本概念
Polygon zkEVM 基本概念
2022-08-04 19:08:00 【mutourend】
1. 引言
前序博客有:
Polygon zkEVM为zk-rollup layer 2扩容方案,其:
- execute smart contracts transparently
- publish zero-knowledge validity proof
- 与以太坊虚拟机opcode完全兼容——为此需重建所有EVM opcodes,从而支持transparent deployment of any existing Ethereum smart contract。
开源代码见:
各代码库有:
| Core Repos | Specific Tools & Libraries | Generic Tools & Libraries |
|---|---|---|
| zkevm-proverjs | zkevm-commonjs | pilcom |
| zkevm-rom | zkasmcom | pil-stark |
| zkevm-prover | zkevm-testvectors | |
| zkevm-node | zkevm-storagerom | |
| zkevm-contracts | ||
| zkevm-bridge-service | ||
| zkevm-bridge-ui | ||
| zkevm-doc |
2. EVM Arithmetization
证明某EVM交易执行正确的第一步是:
- 构建一个合适的execution trace。
所谓execution trace,是指满足EVM processing约束的一组值。将execution trace以矩阵表示,每列具有一个name。将每列插值为一个多项式,将execution的正确性 最终reduce为 验证多项式之间(列之间) 的一组identities。设计合适的列和identities的过程 称为 arithmetization。
Polygon zkEVM提供了an efficient arithmetization of the EVM。
3. Executor, zkASM 和 zkProver
由Executor负责创建execution trace。
Executor的输入有:
- 1)a batch of 交易
- 2)a chain ID
- 3)代表该链zkEVM previous state的Merkle tree root
- 4)代表这些交易执行之后的该链zkEVM new state的Merkle tree root
- 5)values of the current state of the zkEVM,以构建proof
Executor本质上是一种名为zkASM的汇编语言解释器。
使用zkASM语言来构建名为zkROM的程序,Executor运行zkROM程序来提供合适的execution trace。
在zkROM程序中,每个EVM opcode都以一组zkASM指令集来实现。
每个zkASM指令利用了execution trace矩阵中的一行,又名zkEVM的一个“step”。
Executor为zkProver的一部分,zkProver为Polygon zkEVM的核心部件。
zkProver与节点和Database(DB)之间的交互流程为: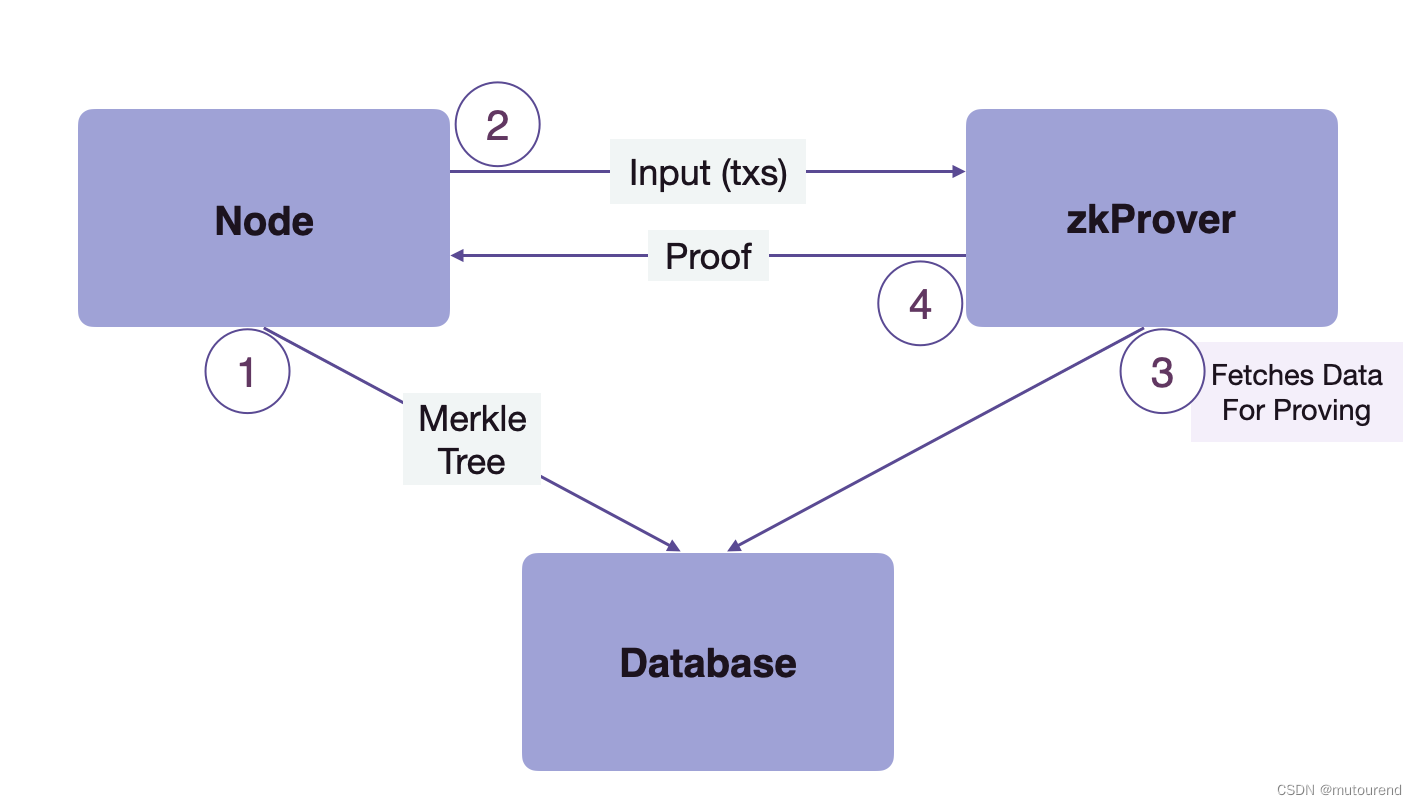
- 1)节点将Ethereum state content和EVM Merkle trees发送到DB并存储。
- 2)节点将input batch of transactions发送到zkProver。
- 3)zkProver访问DB,获取 为节点发送的transaction batch 生成verifiable proof 所需的信息。
- 4)zkProver为交易生成证明,将proof发回给节点。
4. Polynomial Identity Language(PIL)
Polynomial Identity Language(PIL)为定义state machine execution trace约束的领域特定语言。
PIL用于:
- 定义execution trace多项式name
- 描述多项式identities
- 描述多项式之间关系
以满足execution是正确的。
5. Modular Design
对于如EVM这样的复杂state machine,其execution trace对应的列数量和identities数量可达数千。而管理如此庞大的矩阵将是非常复杂且难处理的。
为简化,Polygon zkEVM使用divide and conquer技术,将execution trace切分为更小的矩阵。
使用名为plookup的proving技术,使得一个矩阵的行 可 关联到 另一矩阵的行 成为可能。
此外,还使用了:
- inclusion:检查某矩阵的行 被包含 在另一矩阵中。
- permutation:检查某矩阵中的行 与 另一矩阵中的行 相同,只是顺序不同。
PIL语言:
- 使用
namespace关键字来命名execution trace中切分的每个矩阵的列。 - 使用
in关键字来定义inclusion。 - 使用
is关键字来定义permutation。
Polygon zkEVM中,会将execution trace切分为:
- 一个主矩阵:又名main state machine。
- 多个二级矩阵:又名secondary state machine。
借助divide and conquer技术:
- Polygon zkEVM中包含了不同的connected state machine。
- 每个state machine致力于证明某特定task的execution。
- 不同state machines之间的相关列(polynomials)使用inclusion proof(with plookup)来关联。
6. 一个例子——Fibonacci state machine
Fibonacci序列: a 1 , a 2 , … , a n \mathbf{a_1, a_2, \dots , a_n} a1,a2,…,an,满足 a i + 1 = a i − 1 + a i \mathbf{ a_{i+1} = a_{i-1} + a_i } ai+1=ai−1+ai。
如具有12个成员的序列:
0 , 1 , 1 , 2 , 3 , 5 , 8 , 13 , 21 , 34 , 55 , 89 , … \mathbf{ \ \ 0,\ \ 1,\ \ 1,\ \ 2,\ \ 3,\ \ 5,\ \ 8,\ \ 13,\ \ 21,\ \ 34,\ \ 55,\ \ 89,\ \ \dots } 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, …
很容易检查发现 377 \mathbf{377} 377和 987 \mathbf{987} 987是Fibonacci 序列成员。但若要判断 12 , 586 , 269 , 025 \mathbf{ 12,586,269,025 } 12,586,269,025是否为序列成员,则需要一个公式 或 计算机程序——本文以state machine密码学工具来实现。
6.1 Fibonacci State Machine
具有寄存器 A = ( A 1 , A 2 , … , A l ) \mathbf{A} = ( A_1, A_2, \dots , A_l ) A=(A1,A2,…,Al)和 B = ( B 1 , B 2 , … , B l ) \mathbf{B} = ( B_1, B_ 2, \dots , B_l ) B=(B1,B2,…,Bl)的状态机,第 i i i个状态为 ( A i , B i ) (A_i,B_i) (Ai,Bi),初始状态为 A 1 = 0 , B 1 = 1 A_1=0,B_1=1 A1=0,B1=1。
A 和 B \mathbf{A}和\mathbf{B} A和B寄存器均包含了Fibonacci序列,只是 B \mathbf{B} B中的序列为one step ahead of A \mathbf{A} A,二者具有如下关系:
A i + 1 = B i , B i + 1 = A i + B i . \begin{aligned} A_{i+1} &= B_i , \\ B_{i+1} &= A_i + B_i. \end{aligned} Ai+1Bi+1=Bi,=Ai+Bi.
接下来,是将这些寄存器以多项式表示,并最终引入多项式承诺机制来构建该membership密码学工具。
6.1.1 polynomial identities
区块链传统中,将2个寄存器的多项式表示为 Z p [ x ] \mathbb{Z}_p[x] Zp[x],其系数源自a prime field Z p \mathbb{Z}_p Zp。
将多项式evaluate over subgroup of H = { ω , ω 2 , ω 3 , … , ω 8 = 1 } = * ω * H = \{\omega,\omega^2,\omega^3,\dots,\omega^8 = 1\} = \langle\omega\rangle H={ ω,ω2,ω3,…,ω8=1}=*ω* of order 8 8 8。
定义多项式 P ( x ) P(x) P(x)和 Q ( x ) Q(x) Q(x)为:
P ( ω i ) = A i , Q ( ω i ) = B i . P(\omega^i) = A_i, \\ Q(\omega^i) = B_i. P(ωi)=Ai,Q(ωi)=Bi.
H H H中的每个 x x x形式为 x = ω i x=\omega^i x=ωi for some i i i,从而有:
P ( x ω ) = P ( ω i + 1 ) = A i + 1 , Q ( x ω ) = Q ( ω i + 1 ) = B i + 1 . \begin{aligned} P(x\omega) &= P(\omega^{i + 1}) = A_{i+1}, \\ Q(x\omega) &= Q(\omega^{i+1}) = B_{i+1}. \end{aligned} P(xω)Q(xω)=P(ωi+1)=Ai+1,=Q(ωi+1)=Bi+1.
将关系 A i + 1 = B i A_{i+1} = B_i Ai+1=Bi and B i + 1 = A i + B i B_{i+1} = A_i + B_i Bi+1=Ai+Bi代入,获得如下polynomial identities:
P ( x ω ) = A i + 1 = B i = Q ( ω i ) = ∣ H Q ( x ) , Q ( x ω ) = B i + 1 = A i + B i = P ( ω i ) + Q ( ω i ) = ∣ H P ( x ) + Q ( x ) . \begin{aligned} P(x\omega) &= A_{i+1} = B_i = Q(\omega^i) = \bigg\lvert_H Q(x), \\ Q(x\omega) &= B_{i+1} = A_i + B_i = P(\omega^i) + Q(\omega^i) = \bigg\lvert_H P(x) + Q(x). \end{aligned} P(xω)Q(xω)=Ai+1=Bi=Q(ωi)=∣∣HQ(x),=Bi+1=Ai+Bi=P(ωi)+Q(ωi)=∣∣HP(x)+Q(x).
即:
P ( x ω ) = ∣ H Q ( x ) , Q ( x ω ) = ∣ H P ( x ) + Q ( x ) . \begin{aligned} P(x\omega) &= \bigg\lvert_H Q(x), \\ Q(x\omega) &= \bigg\lvert_H P(x) + Q(x). \end{aligned} P(xω)Q(xω)=∣∣HQ(x),=∣∣HP(x)+Q(x).
6.1.2 Non-cyclic Polynomial Identities Problem
若以上这些polynomial identities可准确表达2个寄存器,则Fibonacci序列中的每个成员均可满足该identities。
注意, H H H的定义并未限定 i ≤ 8 i\leq 8 i≤8,若设置 i = 27 i=27 i=27,则 ω 27 \omega^{27} ω27 is in H H H,因为 ω 27 = w 8 ⋅ ω 8 ⋅ ω 8 ⋅ ω 3 = 1 ⋅ 1 ⋅ 1 ⋅ ω 3 = ω 3 \omega^{27}=w^8 \cdot \omega^8 \cdot \omega^8 \cdot \omega^3 = 1 \cdot 1 \cdot 1 \cdot \omega^3 = \omega^3 ω27=w8⋅ω8⋅ω8⋅ω3=1⋅1⋅1⋅ω3=ω3。
但是不限定 i i i值,以上polynomial identities会有问题。如令 x = ω 8 x=\omega^8 x=ω8,有:
- 对于第一个identity有:
P ( x ω ) = P ( ω 8 ⋅ ω ) = P ( ω 1 ) = A 1 = 0 , but Q ( x ) = Q ( w 8 ) = B 8 = 21 ≠ 0. \begin{aligned} &P(x \omega) = P(\omega^8 \cdot \omega) = P(\omega^1) = A_1 = 0,\ \ \text{but} \\ &Q(x) = Q(w^8) = B_8 = 21 \not= 0. \end{aligned} P(xω)=P(ω8⋅ω)=P(ω1)=A1=0, butQ(x)=Q(w8)=B8=21=0. - 对于第二个identity有:
Q ( x ω ) = Q ( ω ) = B 1 = 1 P ( x ) = P ( ω 8 ) + Q ( ω 8 ) = 21 + 13 = 34 ≠ 1. \begin{aligned} &Q(x \omega) = Q(\omega) = B_1 = 1 \\ &P(x) = P(\omega^8) + Q(\omega^8) = 21 + 13 = 34 \not= 1. \end{aligned} Q(xω)=Q(ω)=B1=1P(x)=P(ω8)+Q(ω8)=21+13=34=1.
这意味着,尽管 H H H是cyclic的,但是identities并不是cyclic的,polynomial identities 与 Fibonacci state machine寄存器 并不匹配。
为此,需要引入纠错多项式 R ( x ) R(x) R(x),使得polynomial identities也是cyclic的。纠错多项式也必须in Z p [ x ] \mathbb{Z}_p[x] Zp[x]。
6.1.3 Correcting Errors in Polynomial Identities
为Fibonacci state machine引入第三个寄存器 C = ( C 1 , C 2 , … , C l ) \mathbf{C} = ( C_1, C_2, \dots , C_l) C=(C1,C2,…,Cl),设置该寄存器的值为 C = ( 1 , 0 , 0 , … , 0 ) \mathbf{C} = ( 1, 0, 0, \dots , 0) C=(1,0,0,…,0)。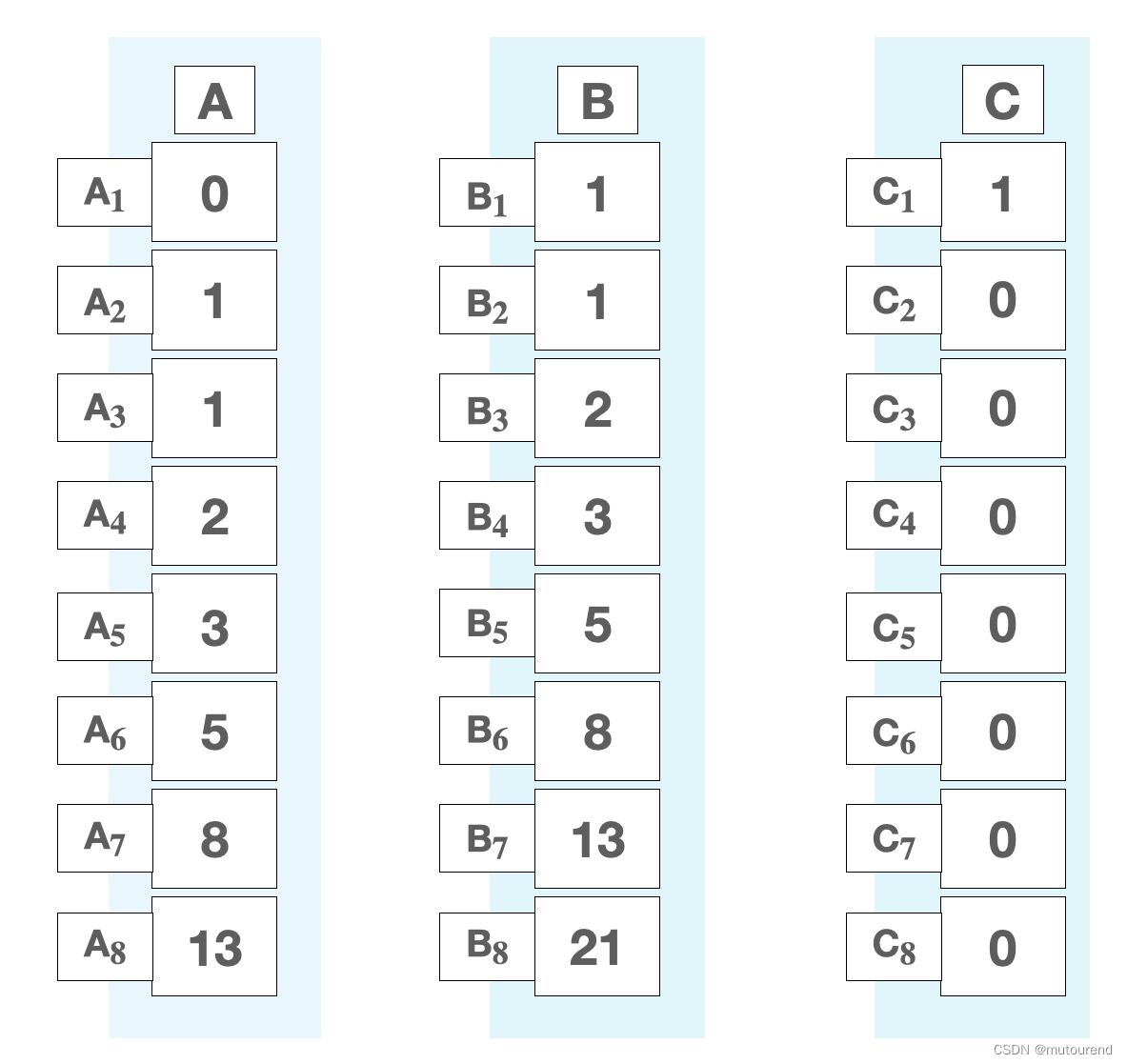
将纠错多项式 R ( x ) R(x) R(x)定义为:
R ( ω i ) = C i . R(\omega^i) = C_i. R(ωi)=Ci.
即:
R ( ω i ) = C i = 1 , if i m o d 8 = 1 , R ( ω i ) = C i = 0 , otherwise . \begin{aligned} R(\omega^i) &= C_i = 1, \text{ if }\ \ i \mod 8 = 1 , \\ R(\omega^i) &= C_i = 0, \text{ otherwise}. \end{aligned} R(ωi)R(ωi)=Ci=1, if imod8=1,=Ci=0, otherwise.
将纠错多项式 R ( x ) R(x) R(x)嵌入到之前的polynomial identities,有:
P ( x ω ) = ∣ H Q ( x ) ( 1 − R ( x ω ) ) , Q ( x ω ) = ∣ H ( P ( x ) + Q ( x ) ) ( 1 − R ( x ω ) ) + R ( x ω ) \begin{aligned} P(x \omega) &= \bigg\lvert_H Q(x) \big( 1 - R(x \omega) \big), \\ Q(x \omega) &= \bigg\lvert_H \big( P(x) + Q(x) \big) \big( 1 - R(x \omega) \big) + R(x \omega) \end{aligned} P(xω)Q(xω)=∣∣HQ(x)(1−R(xω)),=∣∣H(P(x)+Q(x))(1−R(xω))+R(xω)
接下来,仍然设置 x = ω 8 x=\omega^8 x=ω8,来检查新的polynomial identities是否是cyclic的:
- 对于第一个identity有:
L H S = P ( x ω ) = P ( ω 8 ⋅ ω ) = P ( ω 1 ) = A 1 = 0 , R H S = Q ( x ) ( 1 − R ( x ω ) ) = Q ( ω 8 ) ( 1 − R ( ω 8 ⋅ ω ) ) = A 8 ( 1 − R ( ω ) ) = 13 ( 1 − 1 ) = 0. \begin{aligned} LHS &= P(x \omega) = P(\omega^8 \cdot \omega) = P(\omega^1) = A_1 = 0, \\ RHS &= Q(x) \big( 1 - R(x \omega) \big) = Q(\omega^8) \big( 1 - R(\omega^8 \cdot \omega) \big) = A_8 \big( 1 - R(\omega) \big) = 13 \big( 1 - 1 \big) = 0. \end{aligned} LHSRHS=P(xω)=P(ω8⋅ω)=P(ω1)=A1=0,=Q(x)(1−R(xω))=Q(ω8)(1−R(ω8⋅ω))=A8(1−R(ω))=13(1−1)=0.
因此当 x = ω 8 x=\omega^8 x=ω8时,第一个identity成立。很容易检查当 x x x为 H H H中的其它值时,也成立。 - 对于第二个identity有:
L H S = Q ( x ω ) = Q ( ω 8 ⋅ ω ) = Q ( ω 1 ) = B 1 = 1 , R H S = ( P ( ω 8 ) + Q ( ω 8 ) ) ( 1 − R ( ω 8 ⋅ ω ) ) + R ( ω 8 ⋅ ω ) = ( A 8 + B 8 ) ( 1 − R ( ω 1 ) ) + R ( ω 1 ) = ( 13 + 21 ) ( 1 − 1 ) + 1 = 1. \begin{aligned} LHS &= Q(x \omega) = Q(\omega^8 \cdot \omega) = Q(\omega^1) = B_1 = 1 ,\\ RHS &= \big( P(\omega^8) + Q(\omega^8) \big) \big( 1 - R(\omega^8 \cdot \omega) \big) + R(\omega^8 \cdot \omega) \\ &= \big( A_8 + B_8 \big) \big( 1 - R(\omega^1) \big) + R(\omega^1)\\ &= \big( 13 + 21 \big) \big( 1 - 1 \big) + 1 = 1 . \end{aligned} LHSRHS=Q(xω)=Q(ω8⋅ω)=Q(ω1)=B1=1,=(P(ω8)+Q(ω8))(1−R(ω8⋅ω))+R(ω8⋅ω)=(A8+B8)(1−R(ω1))+R(ω1)=(13+21)(1−1)+1=1.
因此当 x = ω 8 x=\omega^8 x=ω8时,第二个identity成立。很容易检查当 x x x为 H H H中的其它值时,也成立。
6.1.4 Varied Initial Conditions
注意,此处不再限定初始条件为 ( A 1 , B 1 ) = ( 0 , 1 ) \big( A_1 , B_1 \big) = \big( 0 , 1 \big) (A1,B1)=(0,1)。
将polynomial identities调整为适于任意初始条件 ( A 1 , B 1 ) \big( A_1 , B_1 \big) (A1,B1):
P ( x ω ) = ∣ H Q ( x ) ( 1 − R ( x ω ) ) + A 1 R ( x ω ) , Q ( x ω ) = ∣ H ( P ( x ) + Q ( x ) ) ( 1 − R ( x ω ) ) + B 1 R ( x ω ) . \begin{aligned} P(x \omega) &= \bigg\lvert_H Q(x) \big( 1 - R(x \omega) \big) + A_1 R(x \omega), \\ Q(x \omega) &= \bigg\lvert_H \big( P(x) + Q(x) \big) \big( 1 - R(x \omega) \big) + B_1 R(x \omega) . \end{aligned} P(xω)Q(xω)=∣∣HQ(x)(1−R(xω))+A1R(xω),=∣∣H(P(x)+Q(x))(1−R(xω))+B1R(xω).
6.1.5 Proving Our State Machine(High level)
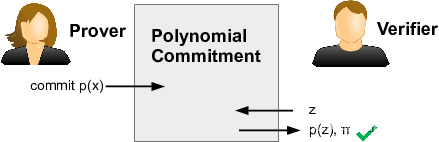
之前的多项式关系可通过如 KZG 和 基于FRI 的多项式承诺来证明。
承诺机制具有binding和hiding属性:
- 1)Binding:一旦commit之后,Prover无法修改多项式。
- 2)Hiding:仅知道承诺值,Verifier无法推导出Prover所commit的具体多项式。
7. 一个例子——Arithmetic State Machine
arithmetic state machine将检查32bit元素的加减乘除运算。
约束中有5个寄存器:
A i ⋅ B i + C i = 2 32 D i + E i . \mathcal{A}_i \cdot \mathcal{B}_i + \mathcal{C}_i = 2^{32} \mathcal{D}_i + \mathcal{E}_i. Ai⋅Bi+Ci=232Di+Ei.
注意,以上五个寄存器均为32bit的。
跟之前类似,将该关系表示为a cyclic polynomial identity at some subgroup H H H of roots of unity of Z p \mathbb{Z}_p Zp:
A ( x ) ⋅ B ( x ) + C ( x ) = 2 32 D ( x ) + E ( x ) . \mathcal{A}(x) \cdot \mathcal{B}(x) + \mathcal{C}(x) = 2^{32} \mathcal{D}(x) + \mathcal{E}(x). A(x)⋅B(x)+C(x)=232D(x)+E(x).
注意,此处需要 enforce A ( x ) \mathcal{A}(x) A(x), B ( x ) \mathcal{B}(x) B(x), C ( x ) \mathcal{C}(x) C(x), D ( x ) \mathcal{D}(x) D(x) 和 E ( x ) \mathcal{E}(x) E(x) 在 H H H 的值均为32bit。
参考资料
边栏推荐
猜你喜欢
随机推荐
mq消息积压怎么对应
正畸MIA微种植体支抗技术中国10周年交流会在沈举办
ECCV 2022 | FPN错位对齐,实现高效半监督目标检测(PseCo)
判断字符串中是否包含中文
开篇-开启全新的.NET现代应用开发体验
JS 问号?妙用
使用.NET简单实现一个Redis的高性能克隆版(二)
MMDetection usage example: from entry to exit
PHP代码审计9—代码执行漏洞
单行、多行文本超出显示省略号
什么是内部客户服务?
PHP代码审计8—SSRF 漏洞
【填空题】130道面试填空题
Usage of collect_list in Scala105-Spark.sql
量化交易机器人系统开发
如何封装 svg
[Latest Information] 2 new regions will announce the registration time for the soft exam in the second half of 2022
LVS+NAT 负载均衡群集,NAT模式部署
c语言进阶篇:自定义类型--结构体
HCIP-R&S By Wakin自用笔记(1)企业网络高级解决方案
![[Sql刷题篇] 查询信息数据--Day1](/img/a7/67b59bd41803dfc07ecb8f00669c29.png)