当前位置:网站首页>NTT(快速数论变换)多项式求逆 一千五百字解析
NTT(快速数论变换)多项式求逆 一千五百字解析
2022-07-26 09:01:00 【秦小咩】
首先我们有
我们对x^n进行向上取整开根号操作,即
我们设
显然
两式相减

故
所以减式构成的多项式在0- 次幂上都是0,否则他们本身就无法被
次幂上都是0,否则他们本身就无法被 整除
整除
根据这一发现
对减式进行平方


进行乘F(x)操作 再由

由此G(x)用NTT求解
# include<iostream>
using namespace std;
typedef long long int ll;
const int mod=998244353,g=3,N=2000000;
int n;
ll a[N],b[N],c[N],rev[N];
ll qp(ll base,ll pow)
{
ll ans=1;
while(pow)
{
if(pow&1)
ans=ans*base%mod;
pow>>=1;
base=base*base%mod;
}
return ans;
}
void init(int k)
{
int len=(1<<k);
for(int i=0;i<len;i++)
{
rev[i]=0;
}
for(int i=0;i<len;i++)
{
rev[i]=(rev[i>>1]>>1)|((i&1)<<(k-1));
}
return ;
}
void NTT(ll *a,int n,int flag)
{
for(int i=0;i<n;i++)
{
if(i<rev[i])
{
swap(a[i],a[rev[i]]);
}
}
for(int h=1;h<n;h<<=1)
{
ll gn=qp(3ll,(mod-1)/(h*2));
if(flag==-1)
gn=qp(gn,mod-2);
for(int j=0;j<n;j+=2*h)
{
ll gg=1;
for(int k=j;k<j+h;k++)
{
ll x=a[k];
ll y=gg*a[k+h]%mod;
a[k]=(x+y)%mod;
a[k+h]=((x-y)%mod+mod)%mod;
gg=gg*gn%mod;
}
}
}
if(flag==-1)
{
ll inv=qp(n,mod-2);
for(int i=0;i<n;i++)
{
a[i]=a[i]*inv%mod;
}
}
}
void work(int pow,ll*a,ll *b)
{
if(pow==1)
{
b[0]=qp(a[0],mod-2);
return ;
}
work((pow+1)>>1,a,b);
int k=1,s=2;
while((1<<k)<pow+pow-1)
{
k++;
s<<=1;
}
init(k);
for(int i=0;i<pow;i++)
{
c[i]=a[i];
}
/*
之所以用c存a,而不对a进行直接操作是因为我们每次递归的
都必须是原数列的a
*/
NTT(c,s,1);
NTT(b,s,1);
for(int i=0;i<s;i++)
{
b[i]=(ll)(2ll-c[i]*b[i]%mod+mod)%mod*b[i]%mod;
}
NTT(b,s,-1);
for(int i=pow;i<s;i++)
{
b[i]=0;
}
return ;
}
int main ()
{
cin>>n;
for(int i=0;i<n;i++)
{
cin>>a[i];
}
work(n,a,b);
for(int i=0;i<n;i++)
{
cout<<b[i]<<" ";
}
return 0;
}
边栏推荐
- PAT 甲级 A1013 Battle Over Cities
- 高数 | 武爷『经典系列』每日一题思路及易错点总结
- Uni app simple mall production
- Flask project learning (I) -- sayhello
- Web概述和B/S架构
- Introduction to AWD attack and defense competition
- 2000年的教训。web3是否=第三次工业革命?
- Zipkin安装和使用
- Day06 operation -- addition, deletion, modification and query
- Day06 homework - skill question 6
猜你喜欢

Cat安装和使用

JS file import of node

Day06 homework -- skill question 1

Day06 operation -- addition, deletion, modification and query
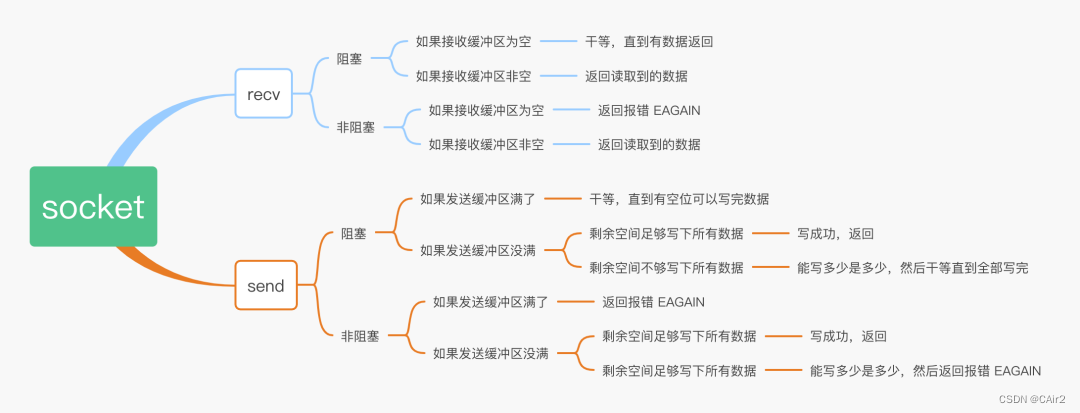
tcp 解决short write问题

Study notes of automatic control principle -- dynamic model of feedback control system

Form form

Okaleido上线聚变Mining模式,OKA通证当下产出的唯一方式

209. Subarray with the smallest length

Unity topdown character movement control
随机推荐
Espressif 玩转 编译环境
Store a group of positive and negative numbers respectively, and count the number of 0 -- assembly language implementation
My meeting of OA project (query)
Learning notes of automatic control principle --- linear discrete system
The lessons of 2000. Web3 = the third industrial revolution?
【数据库 】GBase 8a MPP Cluster V95 安装和卸载
Introduction to excellent verilog/fpga open source project (30) - brute force MD5
What are the differences in the performance of different usages such as count (*), count (primary key ID), count (field) and count (1)? That's more efficient
[database] gbase 8A MPP cluster v95 installation and uninstall
Introduction to AWD attack and defense competition
Datawhale panda book has been published!
ext4文件系统打开了DIR_NLINK特性后,link_count超过65000的后使用link_count=1来表示数量不可知
垂直搜索
Typescript encryption tool passwordencoder
Zipkin安装和使用
优秀的 Verilog/FPGA开源项目介绍(三十零)- 暴力破解MD5
NFT与数字藏品到底有何区别?
Uni app simple mall production
Ueditot_ JSP SSRF vulnerability recurrence
《Datawhale熊猫书》出版了!