数字信号处理

信号的基本运算和概念

信号分为离散信号和连续信号

运算

加，乘法：
对应位置的值相运算
2：
先平移再尺度变化在反转

三种表示方法表示

还有一种添下划线

离散LTI时域系统的分析

判断是否为线性系统（满足均匀特性和叠加特性）

1.两个信号经过系统相加之后，其值等于两个信号单独作用域系统所产生的信号相加。
2.当输入放大一个倍数过后，输出依然放大同样的倍数

eg：

判断是否为时变特性

输入延时n个单位，输出也相应的延时n个单位
eg：

一般的线性非时变系统

信号的频域分析

带限信号的抽样

抽样频率：

工程上的信号抽样（非带限信号的抽样）

理论模型中，系统通过冲击串来抽样，但是工程上冲击信号是不存在的

如何进行非带限信号抽样

实际上的工程是不满足带限条件的，那我们如何来使用抽样定理呢？
加一个抗混的低通滤波器

过程

如果直接对他进行抽样会造成频谱的混叠，叫做混叠误差，因为时域的离散化造成时域的周期化，所以需要经过抗混低通滤波器进行滤波，对其高频分量进行抑制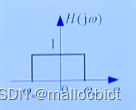

经过滤波之后：
依然有比较小的高频分量，但是不影响大局，会有截断误差（不能直接还原x(t)，只能还原出x1(t)）

截断误差和混叠误差

上者是混叠误差
下者是截断误差
混叠误差要比截断误差大

例题

1.如果直接对非带限信号进行抽样会造成频谱的混叠，叫做混叠误差，此时需要经过抗混低通滤波器进行滤波，对其高频分量进行抑制，然后在进行抽样即可（虽然无法完全还原，但是已经做了极大的优化了）
所以在工程当中都要先加一个抗混的的低通滤波器

如何对未知最高频率下的信号抽样

先以较高的频率进行抽样，如果有很大一部分区域为0的话就说明有裕量，后期再对频率进行减小即可

举个例子：
当以搞得频域进行抽样时，声音会十分清晰，但是以很低的频率进行抽样时声音就会模糊，因为发生了混叠

实现信号的重建

1.重建是信号的时域抽样的逆过程
2.先将离散序列用零界保持输出的连续信号变成图2，再用低通滤波器的平滑滤波重建信号如图3

抽样和重建的时间间隔必须统一

为了保证重建之后的信号正确，必须保证x(t)=xout(t)，所以T1也必须等于T2

当T1=T2时

1.先离散化即按T1间隔抽样得到图2
2.重建的时候使用图2进行重建得到图3
3.将图2的信号进行平滑处理得到图3，图3和图1基本相同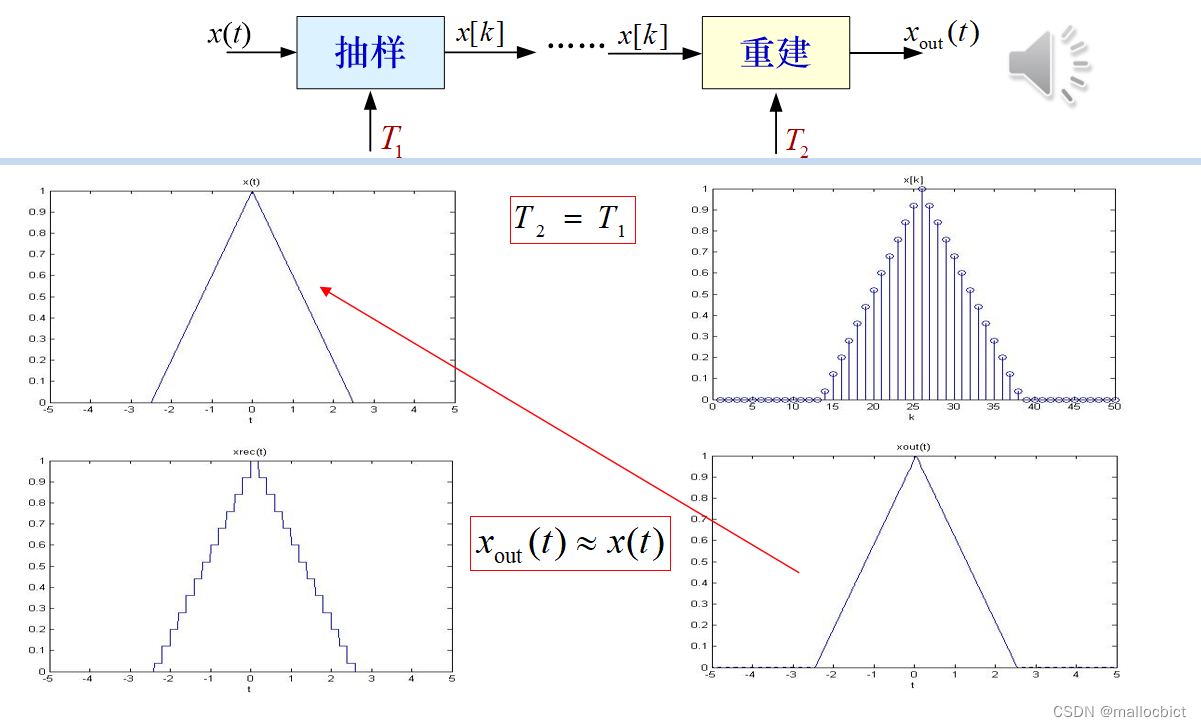

T2=2T1

当图2以T2的时间间隔来重建时，图形会被展宽一倍

T2=1/2*T1

同理被压缩了

信号的抽样和重建例题

离散傅里叶变换（DFT）

DFT就是DFS在一个周期上的取值

引入离散傅里叶变换DFT的原因：

在很多实际操作中无法从数字表达式中得到信号的频谱，而dft可以从理论上得到从时域到频域的映射

时域抽样定理和频域抽样定理

时域抽样定理：频带为F的连续信号f(t)可用一系列离散的采样值f(t1)，f(t1±Δt)，f(t1±2Δt)，…来表示，只要这些采样点的时间间隔Δt≤1/(2F)，便可根据各采样值完全恢复原来的信号f(t)。这是时域采样定理的一种表述方式。
频域抽样定理：

循环卷积和线性卷积

循环卷积定义

例题

快速傅里叶变化（FFT）

基本思想

FFT算法的基本思想： 利用DFT系数的特性，合并DFT运算中的某些项 把长序列DFT→短序列DFT，从而减少运算量。

在数字信号处理中常常需要用到离散傅立叶变换(DFT)，传统的DFT算法算法计算量大，耗时长，不利于计算机实时对信号进行处理。快速的离散傅立叶计算方法——FFT，被发现，离散傅立叶变换才在实际的工程中得到广泛应用。

时间复杂度

对于M维的数据（每一维长度为A，B，C，…），则FFT的时间复杂度为O( ABC*…* log(ABC*…) )

若每一维长度相同，即A=B=C=…=N，则时间复杂度可以简化为O(N^M*logN)

fft的应用

数字图像处理，做快速相关运算，手机打电话，雷达测量速度和方向

数字滤波器

概念

分类

fir：有限脉冲响应
iir：无限脉冲响应

指标

非低通滤波器设计

如何设计非低通滤波器：先转换为低通滤波器，再由低通滤波器转换为其他滤波器

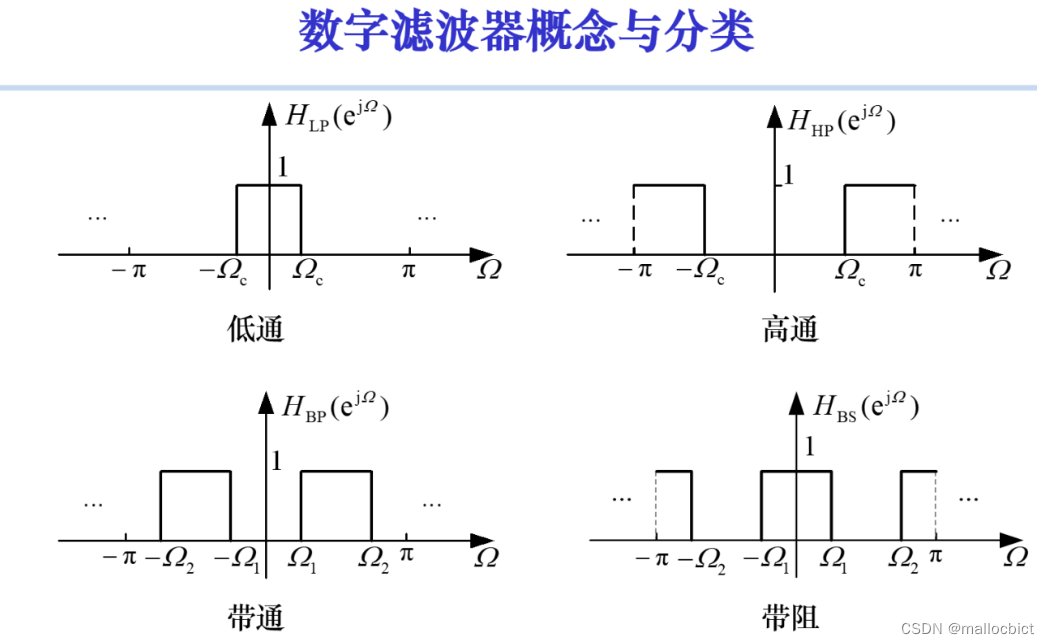
低通到高通的转换

用途

消除噪声降低信噪比，在频带信号中分离信号。从 信号中滤除你不需要的部分，优化信号的质量。