Mathematical Principles of Matrix

Opening Title 1:

Multiplying a matrix on the left represents a transformation of the vector on the right. The vector represents a directional line. The result of the transformation is actually to perform various motions on this line, including: translation, rotation, scaling, and projection.(high-dimensional to low-dimensional), mapping, etc., where mapping is an operation Rn → Rm to increase or reduce dimension (also in the same space) of a vector, so in a broad sense, the meaning of mapping is equivalent to transformation.

Another word that is often mentioned is "linear transformation". Linear transformation ensures that the input straight line (vector) will not be bent during the transformation process, that is, the input is a straight line, and the output is also a straight line.Because matrix transformations are all linear transformations, the "transformation" we are talking about here is actually "linear transformation"

Opening Title 2:

Among various transformations, there is a transformation that has good characteristics - it can make the length of the transformed vector, the inner product between the vectors, distance, angle and many other properties unchanged. This transformation, weIt is called orthogonal transformation, and the matrix used to implement this transformation is called orthogonal matrix, and the characteristics of this transformation are called the invariance of orthogonal transformation.

If there are m vectors, and we regard the vectors as points, then the m points will constitute a space (graphic) with a certain geometric structure. We perform orthogonal transformation on these m points, and the result is intuitive.That is to say, the orthogonal transformation will not stretch and compress the graphics, it can make the transformed graphics maintain the geometric shape of the original graphics, as shown in the following figure, the space composed of ABC is orthogonally transformed to A'B'C',Neither its size nor shape will change.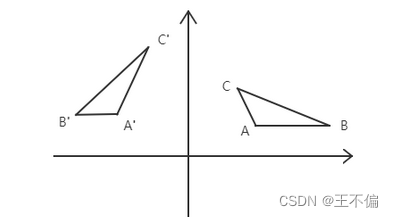

The above orthogonal transformation is an intuitive explanation from the result of the transformation. It can be seen that this transformation has good properties - it can maintain the invariance of the space, and ensure that the original space will not be compressed and stretched.In a nutshell, this transformation will not lose information, because it maintains the internal structure of the original space, which is very useful in engineering.
Original link: https://blog.csdn.net/MoreAction_/article/details/105442932

1. Geometry of Linear Equations and Orthogonalization:

Reference article link: https://www.cnblogs.com/ailitao/p/11047275.html

The essence of the Gram-schmidt orthogonal method is to subtract the projection on other bases, then the rest is the component of the vertical part (vertical means orthogonal)

Similarly, for the included angle between vectors<>, since the length and inner product remain unchanged, the included angle remains unchanged.In the same way, it can also be proved that the distance between vectors does not change

Orthogonal transformations preserve the geometry of space because lengths, angles, and distances remain unchanged.

2.QR decomposition:

A is suitable for both symmetric and asymmetric matrices.
A=QR;
QR decomposition is to decompose the matrix into an orthogonal matrix Q and an upper triangular matrix R, so it is called QR decomposition.The algorithm works for both symmetric and asymmetric matrices.

3. Cholesky decomposition principle:

Premise: A ∈ R (n × n) is a symmetric positive definite matrix,
then: A= L*L^T;
L is a lower triangular matrix L whose diagonal elements are all positive numbers∈ R (n × n) ,

Cholesky decomposition decomposes a matrix into the product of a lower triangular matrix and its conjugate transpose matrix (in the case of the real number bound, this decomposition is like finding the square root).Compared with the general matrix decomposition method for solving equations, Cholesky decomposition is very efficient.

---

---

---

A summary of LU decomposition, Cholesky decomposition, QR decomposition, SVD decomposition, Jordan decomposition decomposition: https://blog.csdn.net/mucai1/article/details/85242098