当前位置:网站首页>码蹄集 - MT3435 · 赋值 - 二分图问题 - 图文讲解
码蹄集 - MT3435 · 赋值 - 二分图问题 - 图文讲解
2022-06-30 18:28:00 【Tisfy】
赋值
时间限制:1秒
空间限制:256M
题目描述
给定一张含有n个结点m条边的无向图,你必须给每个点赋一个点权(必须是1 2 3中的一个),问有多少种不同的赋值方式(这不就是3^n吗???,往下看)
但有一个限制条件:那就是每条边的两个端点奇偶性必须不同
输入描述
第一行输入两个整数n,m
接下来的m行每行两个整数u,v代表u和v之间有一条边
(数据保证没有自环,没有重边,不保证是连通图)
(1<=n,m<=300000,1<=u,v<=n)
输出描述
输入总的方案数,答案可能非常大,结果对1e9+7取模
样例一
输入
4 4
1 2
2 3
3 4
1 4
输出
8
题目分析
二分图简述
这道题本质上就是二分图问题。
二分图也就是说要把一个图的所有节点划分到两个集合 A A A、 B B B中,使得每一条边两端的节点都不在一个集合中。

通俗地讲,所有红色的节点之间不能有边直接相连,所有蓝色的节点之间不能有边直接相连。
如果我们把一个连通图分成了上述集合 A A A和 B B B,那么我们就可以把 A A A中节点全部赋值为奇数, B B B中节点全部赋值为偶数。
因为奇数有 1 1 1和 3 3 3两种,偶数只有 2 2 2这一种,所以赋值方案数为 2 a 2^a 2a,其中 a a a是 A A A中的节点的个数。
同理,我们也可以把 A A A中节点赋值为偶数, B B B中节点赋值为奇数,则又有 2 b 2^b 2b种赋值方案,其中 b b b是集合 B B B中的节点的个数。
综上所述,一个能把节点分成集合 A A A和 B B B的二分图,节点赋值为 1 、 2 、 3 1、2、3 1、2、3且相邻节点奇偶性不同的赋值方案为 2 a + 2 b 2^a+2^b 2a+2b
那么问题就变成了如何把题目给定的图划分成不同的二分图。
划分为二分图
我们可以用 c o l o r [ i ] color[i] color[i]表示节点 i i i的分组情况。 0 0 0代表为分组, 1 1 1代表该节点被划分到了集合 A A A中, 2 2 2代表划分到了集合 B B B中。
遍历每一个节点,如果这个节点还未被划分,那么就将这个节点作为一个新的二分图的“源点”, B F S BFS BFS一遍并统计这个子图的集合 A 、 B A、B A、B中节点的个数。
注意:若 B F S BFS BFS过程中发现了“一条边两端的节点属于同一个集合”的情况,则此图无法划分为二分图,赋值方案数为 0 0 0。(如下图绿色边所示)

结果计算
当我们把这个图划分为不同的二分图后,每个二分图的方案数之积,就是总方案数。

具体实现可参考代码注释
AC代码
// 给定一张含有n个结点m条边的无向图,每条边的两个端点奇偶性必须不同,有多少种不同的赋值方式
#include <bits/stdc++.h>
using namespace std;
#define mem(a) memset(a, 0, sizeof(a))
#define dbg(x) cout << #x << " = " << x << endl
#define fi(i, l, r) for (int i = l; i < r; i++)
#define cd(a) scanf("%d", &a)
typedef long long ll;
const ll mod = 1e9 + 7;
vector<int> a[300010]; // 存图
ll Pow[300010] = {
1}; // Pow[i] = 2^i
int color[300010] = {
0}; // 分组情况,默认值0表示未分组
int main() {
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; i++) {
// 预处理,计算2^i
Pow[i] = (Pow[i - 1] * 2) % mod;
}
for (int i = 0; i < m; i++) {
// 读入图
int l, r;
scanf("%d%d", &l, &r);
a[l].push_back(r);
a[r].push_back(l);
}
ll ans = 1; // 答案
for (int i = 1; i <= n; i++) {
// 遍历所有节点
if (!color[i]) {
// 还没被染色(说明还没有被划分到某个子图中)
int aNode = 0, bNode = 0; // 二分图A、B中的节点个数
queue<int> q; // bfs队列
function<void(int, int)> addOneNode = [&](int thisNode, int thisColor) {
// 处理一个新的节点
color[thisNode] = thisColor; // 标注分组
q.push(thisNode); // 入队
if (thisColor == 1) // 统计集合中节点的个数
aNode++;
else
bNode++;
};
addOneNode(i, 1); // 先处理这个子图的“源点”
while (q.size()) {
// 开始BFS
int thisNode = q.front();
q.pop(); // 队首节点
int toColor = (color[thisNode] == 1 ? 2 : 1); // 它的相邻节点所属的集合
for (int& toNode : a[thisNode]) {
// 遍历这个节点的所有边
if (!color[toNode]) {
// 相邻节点还未被分组
addOneNode(toNode, toColor); // 处理这个相邻节点(划分集合、入队、统计)
}
else {
// 这个相邻节点已经被分组了
if (color[toNode] == color[thisNode]) {
// 并且和这个节点还被分到了一组中
puts("0"); // 无法划分为二分图,方案数为0
return 0;
}
}
}
}
ans = (ans * (Pow[aNode] + Pow[bNode])) % mod; // 各个子图的方案数之积
}
}
cout << ans << endl;
return 0;
}
每周提前更新菁英班周赛题解,点关注,不迷路
原创不易,转载请附上原文链接哦~
Tisfy:https://letmefly.blog.csdn.net/article/details/125537979
边栏推荐
- Go Redis连接池
- 手机炒股开户安全嘛!?
- Cloud Native Landing Practice Using rainbond for extension dimension information
- Task04:集合运算-表的加减法和join等--天池龙珠计划SQL训练营学习笔记
- Lenovo Yoga 27 2022, full upgrade of super configuration
- Brief introduction of Feature Engineering in machine learning
- Memory Limit Exceeded
- Kubernetes----Pod配置容器启动命令
- VS 常用的快捷键指令
- Regular expressions (regular matching)
猜你喜欢

Year after year, why is breaking the data island still the primary task of enterprise development

Influence and requirements of different manufacturing processes on the pad on PCB

ANSI/UL 94 5-V级垂直燃烧试验

Personally test the size of flutter after packaging APK, quite satisfied

浏览器窗口切换激活事件 visibilitychange

20220607 fell below the recommended retail price, and the GPU market is moving towards oversupply

Opencv data type code table dtype
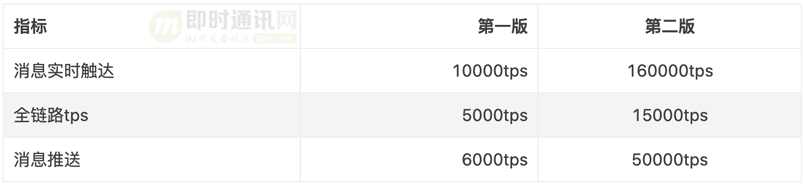
一套十万级TPS的IM综合消息系统的架构实践与思考

Electron 入门

Gateway服务网关
随机推荐
年复一年,为什么打破数据孤岛还是企业发展的首要任务
Regular expressions (regular matching)
How to configure webrtc video stream format playback in the new version of easygbs?
MySQL recursion
Unity technical manual - preliminary performance optimization
MQ组成部分(2022.5.16-5.22)
Unlimited cloud "vision" innovation | the 2022 Alibaba cloud live summit was officially launched
RFFE中MIPI协议
MySQL function to get the full path
MySQL modify data type_ MySQL modify field type [easy to understand]
NBI visual platform quick start tutorial (V) introduction to editor functions and operations
mysql 递归
PO模式简介「建议收藏」
Nodejs 安装与介绍
为什么越来越多的人选择云渲染?
CTF flow analysis common questions (II) -usb flow
Introduction to Po mode "suggestions collection"
Development: how to install offline MySQL in Linux system?
Teach you how to write selenium test cases
20200525 Biotechnology - Sichuan Normal University self taught Biotechnology (undergraduate) examination plan txt