当前位置:网站首页>力扣295. 数据流的中位数
力扣295. 数据流的中位数
2022-06-21 16:53:00 【SS_zico】
中位数是有序列表中间的数。如果列表长度是偶数,中位数则是中间两个数的平均值。
例如,
[2,3,4] 的中位数是 3
[2,3] 的中位数是 (2 + 3) / 2 = 2.5
设计一个支持以下两种操作的数据结构:
void addNum(int num) - 从数据流中添加一个整数到数据结构中。
double findMedian() - 返回目前所有元素的中位数。
示例:
addNum(1)
addNum(2)
findMedian() -> 1.5
addNum(3)
findMedian() -> 2
方法一:插入排序
class MedianFinder {
vector<int> store; // resize-able container
public:
// Adds a number into the data structure.
void addNum(int num)
{
if (store.empty())
store.push_back(num);
else
store.insert(lower_bound(store.begin(), store.end(), num), num); // binary search and insertion combined
}
// Returns the median of current data stream
double findMedian()
{
int n = store.size();
return n & 1 ? store[n / 2] : (store[n / 2 - 1] + store[n / 2]) * 0.5;
}
};
时间复杂度:O(n)
空间复杂度:O(n)
方法二:两个堆
class MedianFinder {
priority_queue<int> lo; // max heap
priority_queue<int, vector<int>, greater<int>> hi; // min heap
public:
// Adds a number into the data structure.
void addNum(int num)
{
lo.push(num); // Add to max heap
hi.push(lo.top()); // balancing step
lo.pop();
if (lo.size() < hi.size()) {
// maintain size property
lo.push(hi.top());
hi.pop();
}
}
// Returns the median of current data stream
double findMedian()
{
return lo.size() > hi.size() ? (double) lo.top() : (lo.top() + hi.top()) * 0.5;
}
};
/** * Your MedianFinder object will be instantiated and called as such: * MedianFinder* obj = new MedianFinder(); * obj->addNum(num); * double param_2 = obj->findMedian(); */
时间复杂度:O(longn)
空间复杂度:O(n)
边栏推荐
- Cann training camp Season 2 - the opening ceremony | it starts at 7:30 tonight on time. You can't miss it!
- Xlrd finds the row of the specified content and its content
- Hain's law and Feynman's learning method
- [real topic of the Blue Bridge Cup provincial tournament 35] scratch water reflection children's programming scratch programming explanation of the real topic of the Blue Bridge Cup provincial tournam
- RMB 18billion, a super master fund was born in Suzhou
- What is the S3 protocol that we are talking about every day? This article takes you to understand the story behind S3
- 大型网站技术架构 | 信息加密技术及密匙安全管理
- Redis6.0 new features (Part 1)
- Node的字符处理
- 云安全日报220621:Ubuntu操作系统发现英特尔微码漏洞,需要尽快升级
猜你喜欢
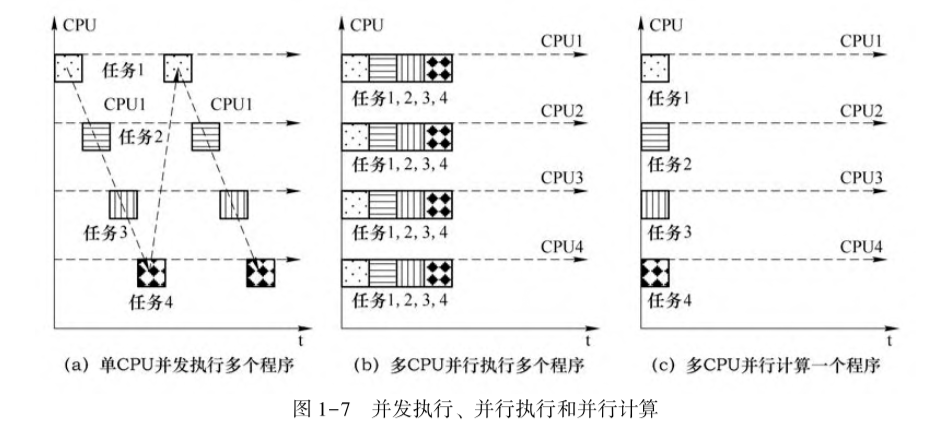
Show you how to distinguish several kinds of parallelism
泰克示波器TCP202电流探头的使用说明

Paper notes ACL 2022 unified structure generation for universal information extraction

System V IPC与POSIX IPC

怎么安装 Laravel
在线文档协作:办公必备高效率神器

Node的json解析

EtherCAT igh 'Fatal Sync Error'——0x002C,0x001A

POSIX信号量

Gartner 网络研讨会 “九问数字化转型” 会后感
随机推荐
编写第一个C#应用程序——Hello, C#
EtherCAT master station based on am4377 controls STM32 slave station
About the basic operation of xlrd Library (for beginners)
Node模块管理描述文件
2022低压电工考试题模拟考试题库及答案
Typescript的通用类型检查
ByteDance proposes a lightweight and efficient new network mocovit, which has better performance than GhostNet and mobilenetv3 in CV tasks such as classification and detection!
The source code of the online live broadcast system enables you to request the list interface and touch the bottom page to load
[Oracle] is there a "time" data type in oracle-- Research on Oracle data types
Live broadcast platform development, live broadcast of each category and single example design display
超分之RLSP
Postman association to complete interface automation test
Tcpserver enable multithreading
Redis配置与优化
System V IPC与POSIX IPC
CentOS使用composer install 报错 - phpunitphpunit 8
PHP连接Mysql8.0报错:Illuminate\Database\QueryException
Runmaide medical passed the listing hearing: it is expected that the loss will increase, with huoyunfei brothers holding about 33%
Laravel实现软删除
Node模块化管理