当前位置:网站首页>第3周 用1层隐藏层的神经网络分类二维数据
第3周 用1层隐藏层的神经网络分类二维数据
2022-08-03 03:28:00 【伍六琪】
课程1 神经网络和深度学习
第2周 用1层隐藏层的神经网络分类二维数据
我是参考此博文,完成该作业。
https://www.heywhale.com/mw/project/5dd3946900b0b900365f3a48
我是在这个博主下的资源
https://blog.csdn.net/u013733326/article/details/79702148
完整的代码实现(过程讲解和练习看上面的链接)
cd D:\software\OneDrive\桌面\吴恩达深度学习课后作业\第三周- 用1层隐藏层的神经网络分类二维数据\resource
D:\software\OneDrive\桌面\吴恩达深度学习课后作业\第三周- 用1层隐藏层的神经网络分类二维数据\resource
# 引包
#sklearn:为数据挖掘和数据分析提供的简单高效的工具。
import numpy as np
import matplotlib.pyplot as plt
from testCases import *
import sklearn
import sklearn.datasets
import sklearn.linear_model
from planar_utils import plot_decision_boundary, sigmoid, load_planar_dataset, load_extra_datasets
%matplotlib inline
np.random.seed(1) # 设定种子使结果一致
#加载数据
X,Y = load_planar_dataset()
#scatter:用于生成一个scatter散点图
#X[0,:]:用于获取X的第一行数据
#s:标量 散点的面积
#c:散点的颜色
#cmap:colormap实例;plt.cm.Spectral:在画图时为不同类别的样本分别分配不同的颜色
plt.scatter(X[0,:],X[1,:],c=Y.reshape(X[0,:].shape),s=40,cmap=plt.cm.Spectral)
<matplotlib.collections.PathCollection at 0x14ed1ac7e10>
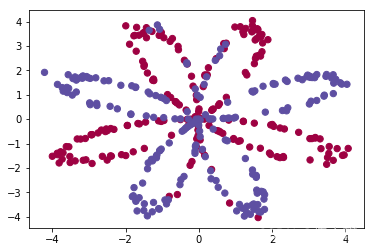
#练习:数据集中有多少个训练示例? 另外,变量“ X”和“ Y”的“shape”是什么?
shape_X = X.shape
shape_Y = Y.shape
m = shape_X[1]
print ('The shape of X is: ' + str(shape_X))
print ('The shape of Y is: ' + str(shape_Y))
print ('I have m = %d training examples!' % (m))
The shape of X is: (2, 400)
The shape of Y is: (1, 400)
I have m = 400 training examples!
1、简单Logistic回归(效果不好)
#sklearn.linear_model.LogisticRegressionCV(): Logistic回归(aka logit,MaxEnt)分类器
#fit(X,Y):监督学习算法,拟合分类器
clf = sklearn.linear_model.LogisticRegressionCV()
clf.fit(X.T, Y.T)
LogisticRegressionCV(Cs=10, class_weight=None, cv=None, dual=False,
fit_intercept=True, intercept_scaling=1.0, max_iter=100,
multi_class=‘ovr’, n_jobs=1, penalty=‘l2’, random_state=None,
refit=True, scoring=None, solver=‘lbfgs’, tol=0.0001, verbose=0)
#绘制此模型的决策边界
#float((np.dot(Y,LR_predictions) + np.dot(1-Y,1-LR_predictions))/float(Y.size)*100)是默认的公式?
#plot_decision_boundary(lambda x: clf.predict(x), X, Y),出错:将Y改为 np.squeeze(Y)
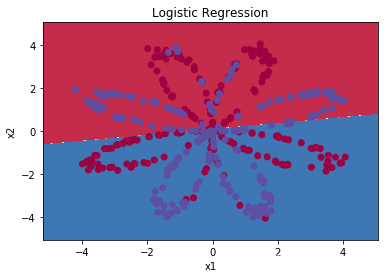
plot_decision_boundary(lambda x: clf.predict(x), X, np.squeeze(Y)) #绘制决策边界
plt.title("Logistic Regression")
LR_predictions = clf.predict(X.T)
print ('逻辑回归的准确性: %d ' % float((np.dot(Y,LR_predictions) + np.dot(1-Y,1-LR_predictions))/float(Y.size)*100) +
'% ' + "(percentage of correctly labelled datapoints)")
逻辑回归的准确性: 47 % (percentage of correctly labelled datapoints)
2、神经网络模型
“训练带有单个隐藏层的神经网络”
提示:
建立神经网络的一般方法是:
- 定义神经网络结构(输入单元数,隐藏单元数等)。
- 初始化模型的参数
- 循环:
- 实现前向传播
- 计算损失
- 后向传播以获得梯度
- 更新参数(梯度下降)
(1) 定义神经网络结构
练习:定义三个变量:
- n_x:输入层的大小
- n_h:隐藏层的大小(将其设置为4)
- n_y:输出层的大小
提示:使用shape来找到n_x和n_y。 另外,将隐藏层大小硬编码为4。
def layer_sizes(X, Y):
n_x = X.shape[0]
n_h = 4
n_y = Y.shape[0]
return (n_x,n_h,n_y)
# 测试layer_sizes函数
x_assess,y_assess = layer_sizes_test_case()
(n_x,n_h,n_y) = layer_sizes(x_assess,y_assess)
print("The size of the input layer is: n_x = " + str(n_x))
print("The size of the hidden layer is: n_h = " + str(n_h))
print("The size of the output layer is: n_y = " + str(n_y))
The size of the input layer is: n_x = 5
The size of the hidden layer is: n_h = 4
The size of the output layer is: n_y = 2
(2) 初始化模型的参数
说明:
请确保参数大小正确。 如果需要,也可参考上面的神经网络图。
使用随机值初始化权重矩阵。
- 使用:np.random.randn(a,b)* 0.01随机初始化维度为(a,b)的矩阵。
将偏差向量初始化为零。
- 使用:np.zeros((a,b)) 初始化维度为(a,b)零的矩阵
# np.random.seed(n)函数用于生成指定随机数。
def initialize_parameters(n_x, n_h, n_y):
np.random.seed(2)
W1 = np.random.randn(n_h,n_x)*0.01
b1 = np.zeros((n_h,1))
W2 = np.random.randn(n_y,n_h)*0.01
b2 = np.zeros((n_y,1))
assert(W1.shape == (n_h,n_x))
assert(b1.shape == (n_h,1))
assert(W2.shape == (n_y,n_h))
assert(b2.shape == (n_y,1))
parameters = {
"W1":W1,
"b1":b1,
"W2":W2,
"b2":b2
}
return parameters
# 测试initialize_parameters函数
n_x,n_h,n_y = initialize_parameters_test_case()
parameters = initialize_parameters(n_x,n_h,n_y)
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
W1 = [[-0.00416758 -0.00056267]
[-0.02136196 0.01640271]
[-0.01793436 -0.00841747]
[ 0.00502881 -0.01245288]]
b1 = [[0.]
[0.]
[0.]
[0.]]
W2 = [[-0.01057952 -0.00909008 0.00551454 0.02292208]]
b2 = [[0.]]
3、循环
说明:
在上方查看分类器的数学表示形式。
你可以使用内置在笔记本中的sigmoid()函数。
你也可以使用numpy库中的np.tanh()函数。
必须执行以下步骤:
1.使用parameters [“ …”]从字典“ parameters”(这是initialize_parameters()的输出)中检索出每个参数。
2.实现正向传播,计算Z[1]A[1] 和 Z[2],A[2] (所有训练数据的预测结果向量)。
向后传播所需的值存储在cache中, cache将作为反向传播函数的输入。
(1)后向传播
def forward_propagation(X, parameters):
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
Z1 = np.dot(W1,X) + b1
A1 = np.tanh(Z1)
Z2 = np.dot(W2,A1)+b2
A2 = sigmoid(Z2)
assert(A2.shape==(1,X.shape[1]))
cache = {
"Z1":Z1,
"A1":A1,
"Z2":Z2,
"A2":A2
}
return A2,cache
#测试forward_propagation函数
#np.mean:求取均值
X_assess,parameters = forward_propagation_test_case()
A2,cache = forward_propagation(X_assess,parameters)
print(np.mean(cache['Z1']) ,np.mean(cache['A1']),np.mean(cache['Z2']),np.mean(cache['A2']))
-0.0004997557777419902 -0.000496963353231779 0.00043818745095914653 0.500109546852431
(2) 练习:实现compute_cost()以计算损失J的值。
def compute_cost(A2, Y, parameters):
m = Y.shape[1]
logprobs = Y*np.log(A2) + (1-Y)* np.log(1-A2)
cost = -1/m * np.sum(logprobs)
cost = np.squeeze(cost)
assert(isinstance(cost, float))
return cost
#测试compute_cost函数
A2, Y, parameters = compute_cost_test_case()
cost = compute_cost(A2, Y, parameters)
print("cost="+str(cost))
cost=0.6929198937761265
(3)前向传播
def backward_propagation(parameters, cache, X, Y):
m = X.shape[1]
W1 = parameters["W1"]
W2 = parameters["W2"]
A1 = cache["A1"]
A2 = cache["A2"]
dZ2 = A2-Y
dW2 = 1/m * np.dot(dZ2,A1.T)
db2 = 1/m * np.sum(dZ2,axis = 1,keepdims = True)
dZ1 = np.dot(W2.T,dZ2) * (1-np.power(A1,2))
dW1 = 1/m * np.dot(dZ1,X.T)
db1 = 1/m * np.sum(dZ1,axis = 1,keepdims = True)
grads = {
"dW1" : dW1,
"db1" : db1,
"dW2" : dW2,
"db2" : db2
}
return grads
# 测试函数 backward_propagation
parameters, cache, X_assess, Y_assess = backward_propagation_test_case()
grads = backward_propagation(parameters, cache, X_assess, Y_assess)
print ("dW1 = "+ str(grads["dW1"]))
print ("db1 = "+ str(grads["db1"]))
print ("dW2 = "+ str(grads["dW2"]))
print ("db2 = "+ str(grads["db2"]))
dW1 = [[ 0.01018708 -0.00708701]
[ 0.00873447 -0.0060768 ]
[-0.00530847 0.00369379]
[-0.02206365 0.01535126]]
db1 = [[-0.00069728]
[-0.00060606]
[ 0.000364 ]
[ 0.00151207]]
dW2 = [[ 0.00363613 0.03153604 0.01162914 -0.01318316]]
db2 = [[0.06589489]]
(4)梯度下降
def update_parameters(parameters, grads, learning_rate = 1.2):
W1 = parameters["W1"]
W2 = parameters["W2"]
b1 = parameters["b1"]
b2 = parameters["b2"]
dW1 = grads["dW1"]
dW2 = grads["dW2"]
db1 = grads["db1"]
db2 = grads["db2"]
W1 = W1 - learning_rate*dW1
W2 = W2 - learning_rate*dW2
b1 = b1 - learning_rate*db1
b2 = b2 - learning_rate*db2
parameters = {
"W1":W1,
"b1":b1,
"W2":W2,
"b2":b2
}
return parameters
# 测试函数 update_parameters
parameters, grads = update_parameters_test_case()
parameters = update_parameters(parameters, grads)
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
W1 = [[-0.00643025 0.01936718]
[-0.02410458 0.03978052]
[-0.01653973 -0.02096177]
[ 0.01046864 -0.05990141]]
b1 = [[-1.02420756e-06]
[ 1.27373948e-05]
[ 8.32996807e-07]
[-3.20136836e-06]]
W2 = [[-0.01041081 -0.04463285 0.01758031 0.04747113]]
b2 = [[0.00010457]]
4、在nn_model()中集成1、2和3部分中的函数
def nn_model(X,Y,n_h, num_iterations = 10000, print_cost=False):
# 1:layer_sizes(X, Y)
np.random.seed(3)
n_x = layer_sizes(X, Y)[0]
n_y = layer_sizes(X, Y)[2]
# 2:initialize_parameters(n_x,n_h,n_y)
parameters = initialize_parameters(n_x,n_h,n_y)
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
# 3:forward_propagation(X,parameters)
for i in range(0,num_iterations):
A2, cache = forward_propagation(X, parameters)
cost = compute_cost(A2,Y,parameters)
grads = backward_propagation(parameters, cache, X, Y)
parameters= update_parameters(parameters, grads)
if print_cost and i % 1000 == 0:
print("Cost after iteration %i: %f" %(i, cost))
return parameters
#测试函数 nn_model
X_assess,Y_assess = nn_model_test_case()
parameters = nn_model(X_assess,Y_assess,4, num_iterations = 10000, print_cost=False)
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
W1 = [[-0.37522457 -0.66412896]
[ 0.01244063 0.01658567]
[-0.17662459 -0.2802151 ]
[-0.0120937 -0.01635778]]
b1 = [[-1.14066663]
[-1.69949907]
[-1.36650217]
[-1.81190248]]
W2 = [[ 3.60822483e-17 -2.77555756e-17 2.22044605e-17 6.10622664e-17]]
b2 = [[-0.26467576]]
5、预测
使用你的模型通过构建predict()函数进行预测。
使用正向传播来预测结果。
def predict(parameters , X):
A2,cache = forward_propagation(X,parameters)
predictions = np.round(A2)
return predictions
#测试函数predict
parameters,X_assess = predict_test_case()
predictions = predict(parameters , X_assess)
print("predictions mean = " + str(np.mean(predictions)))
predictions mean = 0.6666666666666666
# 集成测试数据
parameters = nn_model(X,Y,n_h =4, num_iterations = 10000, print_cost=True)
plot_decision_boundary(lambda x :predict(parameters,x.T),X,Y)
plt.title("Decision Boundary for hidden layer size " + str(4))
Cost after iteration 0: 0.693048
Cost after iteration 1000: 0.288083
Cost after iteration 2000: 0.254385
Cost after iteration 3000: 0.233864
Cost after iteration 4000: 0.226792
Cost after iteration 5000: 0.222644
Cost after iteration 6000: 0.219731
Cost after iteration 7000: 0.217504
Cost after iteration 8000: 0.219504
Cost after iteration 9000: 0.218571Text(0.5,1,'Decision Boundary for hidden layer size 4')
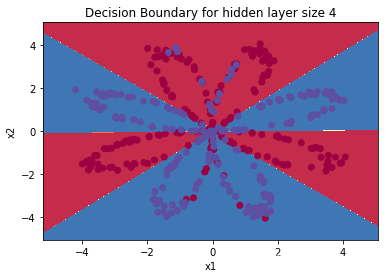
predictions = predict(parameters,X)
print ('Accuracy: %d' % float((np.dot(Y,predictions.T) + np.dot(1-Y,1-predictions.T))/float(Y.size)*100) + '%')
Accuracy: 90%
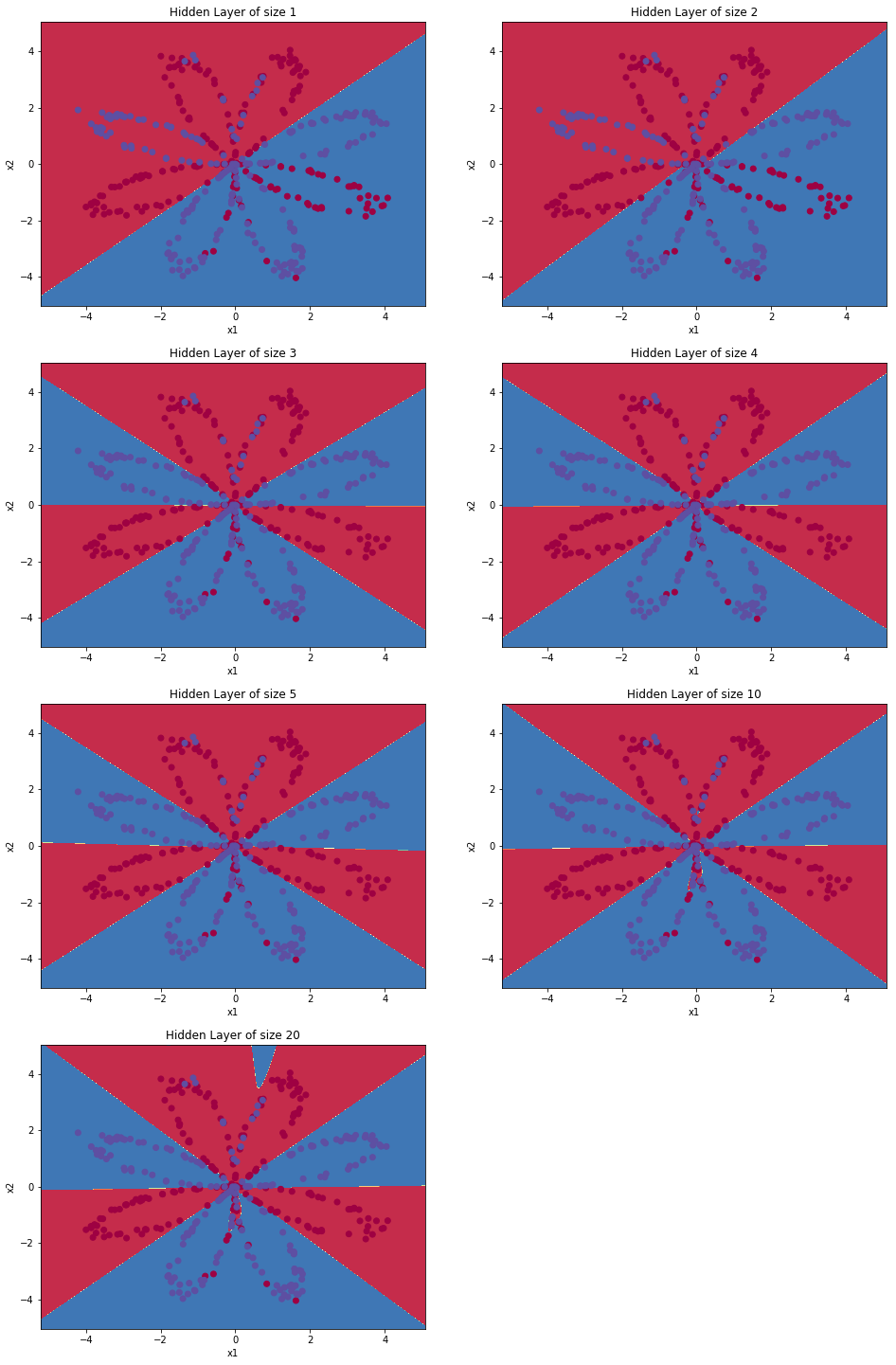
#拓展1:调整隐藏层大小
plt.figure(figsize=(16, 32))
hidden_layer_sizes = [1, 2, 3, 4, 5, 10, 20]
for i, n_h in enumerate(hidden_layer_sizes):
plt.subplot(5, 2, i+1)
plt.title('Hidden Layer of size %d' % n_h)
parameters = nn_model(X, Y, n_h, num_iterations = 5000)
plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y)
predictions = predict(parameters, X)
accuracy = float((np.dot(Y,predictions.T) + np.dot(1-Y,1-predictions.T))/float(Y.size)*100)
print ("Accuracy for {} hidden units: {} %".format(n_h, accuracy))
Accuracy for 1 hidden units: 67.5 %
Accuracy for 2 hidden units: 67.25 %
Accuracy for 3 hidden units: 90.75 %
Accuracy for 4 hidden units: 90.5 %
Accuracy for 5 hidden units: 91.25 %
Accuracy for 10 hidden units: 90.25 %
Accuracy for 20 hidden units: 90.0 %
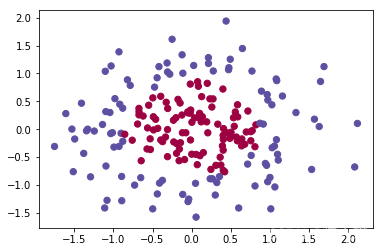
# 拓展2:新的数据集
noisy_circles, noisy_moons, blobs, gaussian_quantiles, no_structure = load_extra_datasets()
datasets = {
"noisy_circles": noisy_circles,
"noisy_moons": noisy_moons,
"blobs": blobs,
"gaussian_quantiles": gaussian_quantiles}
### START CODE HERE ### (choose your dataset)
dataset = "gaussian_quantiles"
### END CODE HERE ###
X, Y = datasets[dataset]
X, Y = X.T, Y.reshape(1, Y.shape[0])
# make blobs binary
if dataset == "blobs":
Y = Y%2
# Visualize the data
plt.scatter(X[0, :], X[1, :], c=Y.reshape(X[0,:].shape), s=40, cmap=plt.cm.Spectral);
边栏推荐
- DPDK mlx5 驱动使用报错
- vant-field中colon属性为true报错
- Jincang Database OCCI Migration Guide (5. Program Development Example)
- ClickHouse常用函数速查大全
- shell之条件语句(条件测试、if语句,case语句)
- uniapp运行到手机,基座提示本应用无法独立运行,需要与hbuilderX 搭配使用
- IPv4编址;A类、B类、C类、D类、E类IP地址(IP地址;网络地址和主机地址;子网掩码;网关;广播地址;)
- Senior ClickHouse -
- 【每日一题】622. 设计循环队列
- ROS2自学笔记:机器视觉基础
猜你喜欢
随机推荐
金仓数据库 MySQL 至 KingbaseES 迁移最佳实践(3. MySQL 数据库移植实战)
企业上云规划与云原生环境设计
Pro * C Jin Cang database migration guide (4) KingbaseES Pro * C migration guide)
金仓数据库 OCCI 迁移指南(5. 程序开发示例)
voliate关键字
【动态规划--01背包】HJ16 购物单
数商云供应链集成系统开发方案:多行业集成平台管理自动化
软件测试技术之如何编写测试用例(2)
Kotlin multiplication, how do I multiply smaller and smaller?
vscode access denied to unins000.exe
软件测试个人求职简历该怎么写,模板在这里
钢铁电商行业方案:钢铁工业产品全生命周期管理解决方案
Task Scheduler 计划定时任务,修改时报错: One or more of the specified arguments are not valid
ESP8266-Arduino编程实例-LED点阵驱动(基于Max7219)
22 ES6 knowledge points
js的组成及js样式
【GO记录】从零开始GO语言——用GO语言做一个示波器(二)基于arduino的简易示波器
2022-08-02 顾宇佳 学习笔记 多线程
Auto. Js scripts run time calculated Pro
【TA-霜狼_may-《百人计划》】美术2.5 模型常见问题及规范