In depth description of Weibull distribution (1) principle and formula

1 Preface ：

The Weber distribution is often used to evaluate failure （Failure） perhaps , On the contrary , reliability , Tools for measuring . His goal is to build a failure analysis model , Or build a failure analysis Pattern.
This chapter introduces the Weibull distribution (weibull distribution) Cumulative distribution function of CDF\ Density distribution function PDF\ Mathematical expectation EDF Basic formula of 、 Parameters 、 Basic graphics and derivation .
When introducing the concept of formula , Most of the general concepts in probability theory are explained in the concept section .

Application scenarios of Weber distribution ： Include ,【 Industrial manufacturing 、 Study the relationship between production process and transportation time 、 Extreme value theory 、 Forecast the weather 、 Reliability and failure analysis 、 The radar system models the received clutter signal according to the distribution . Fitting degree in wireless communication technology , Relative exponential attenuation channel model ,Weibull The attenuation model has a good fit to the attenuation channel modeling . Quantifying repeated claims in life insurance models 、 Predict technological change 、 The wind speed is well matched with the actual situation because of the curve shape , Used to describe the distribution of wind speed .】

2 Cumulative distribution function of Weber distribution （CDF-Cumulative Distribution Function）：

【 case , This chapter CDF It means CDF of weibull 】
【CDF In fact, that is PDF Integral , See attached reference definitions 】

2.1 Cumulative distribution function of two parameter Weber distribution and its derivation

【Franklin case , On display CDF Before the formula , I have to mention the formulas in some degree knowledge in China , The Greek alphabet is completely different from that of foreign countries , However , Many Greek letters have specific meanings in use , This paper adopts a general expression formula 】
$$F(x)=\{\begin{array}{ccc}1-e^{-(\frac{x}{\lambda }{)}^k}& x\ge 0& \\ 0& x<0& \end{array}【somedegreesurfacereachtype】F(x)=\{\begin{array}{ccc}1-e^{-(\frac{x}{\eta }{)}^{\beta }}& x\ge 0& \\ 0& x<0& \end{array}【throughusesurfacereachtype】$$
【 Some degree 】

• x Is a random variable (continuous random variable)
• k For shape parameters (shape parameter）
• λ Zoom factor (scale parameter）

【 Universal 】

• x Is a random variable (continuous random variable)[ case , Mostly t describe ]
• β For shape parameters (shape parameter）
• η Zoom factor (scale parameter）
  ​

【 If we put t As representative Failure Random variable of , The cumulative distribution function represents the life cycle of a system （ Because it depends on time ） in failure The cumulative probability of random time 】
$$F(t)=1-e^{-(\frac{t}{\eta }{)}^{\beta }}(t>0)$$
obviously , Because we defined F(t) As a function of the effectiveness rate of the system (failure rate function), So the corresponding , System reliability （Reliability） The function of is ：
【 Failure and reliability are two completely random variables , all , In fact, it can be defined in reverse , therefore , They also call each other reverse Weibull Distribution That's what I'm saying 】
$$R(t)=1-F(t)$$
That is to say ,

$$R(t)=e^{-(\frac{t}{\eta }{)}^{\beta }}(t>0)$$

$$Onchart,displayin了F(t)R(t)staystructurebuildlosseffectchartOfIt\; meansThe\; righteous,redcolorbysystemsystemsodisabledOfGeneralrate,greencolorbysystemsystemsteadysetOfGeneralrate$$
【 obviously , This is also the meaning of the cumulative distribution function . The vertical coordinate in the figure above is the probability of the problem , The abscissa is time （t）】

The Cumulative Distribution Function (CDF), of a real-valued random variable X, evaluated at x, is the probability function that X will take a value less than or equal to x.

【 Cumulative distribution function is to calculate all possible probabilities that random variables are less than or equal to a certain value 】

2.2 Three parameter Weber distribution cumulative distribution function

$$F(x)=\{\begin{array}{ccc}1-e^{-(\frac{x-\gamma }{\eta }{)}^{\beta }}& x\ge 0& \\ 0& x<0& \end{array}【throughusesurfacereachtype】$$

• x Is a random variable (continuous random variable)[ case , Mostly t describe ]
• β State for shape (shape parameter）
• η Zoom factor (scale parameter）
  - γ Positional arguments (location parameter) Also known as threshold Parameters
  【 case , One more position parameter 】
  【 case ,CDF In some analyses , Also known as Weibull probability plot】

3 Probability density function of Weber distribution （PDF-Probability density function）：

【 case , This chapter PDF It means PDF of weibull 】

3.1 PDF The derivation of

PDF In fact, that is CDF Differential of , You can tell by name that , One is the cumulative function , One is the density function .
Can be worked out mathematically PDF The expression of ：

$$\frac{\mathrm{d}F(t)}{\mathrm{d}x}=f(t)$$
According to a simple calculus formula ,
$$\frac{\mathrm{d}(1)}{\mathrm{d}x}=0,\frac{\mathrm{d}(e^x)}{\mathrm{d}x}=e^x,\frac{\mathrm{d}(e^{ax})}{\mathrm{d}x}=a{e}^{ax},\frac{\mathrm{d}(a{x}^k)}{\mathrm{d}x}=a{x}^{k-1}{e}^{a{x}^k}$$
Available ,
$$F(t)=1-e^{-(\frac{t}{\eta }{)}^{\beta }},f(t)=\frac{\mathrm{d}F(t)}{\mathrm{d}x}=0-\frac{\mathrm{d}{e}^{-(\frac{t}{\eta }{)}^{\beta }}}{\mathrm{d}x}$$
Make ,
$$a=-(\frac{1}{\eta }{)}^{\beta },\frac{\mathrm{d}(e^{ax})}{\mathrm{d}x}=a{e}^{ax}$$
$$f(t)=-(\frac{1}{\eta }{)}^{\beta }.t^{\beta -1}.\beta .e^{-(\frac{t}{\eta }{)}^{\beta }}=\frac{\beta }{{\eta }^{\beta }}{t}^{\beta -1}{e}^{-(\frac{t}{\eta }{)}^{\beta }}$$
thus , We get the expression of the density function of the Weber distribution with the following two parameters ：

3.2 Two parameters Weibull Distribution Of PDF

$$f(t;\beta ,\eta )=\{\begin{array}{ccc}\frac{\beta }{{\eta }^{\beta }}{t}^{\beta -1}{e}^{-(\frac{t}{\eta }{)}^{\beta }}& t,\beta ,\eta >0& \\ 0& ItsHelovecondition& \end{array}$$

• β (shape parameter shape parameter ) Also known as weibull slope Weber slope
• η (scale parameter Scaling parameters ）
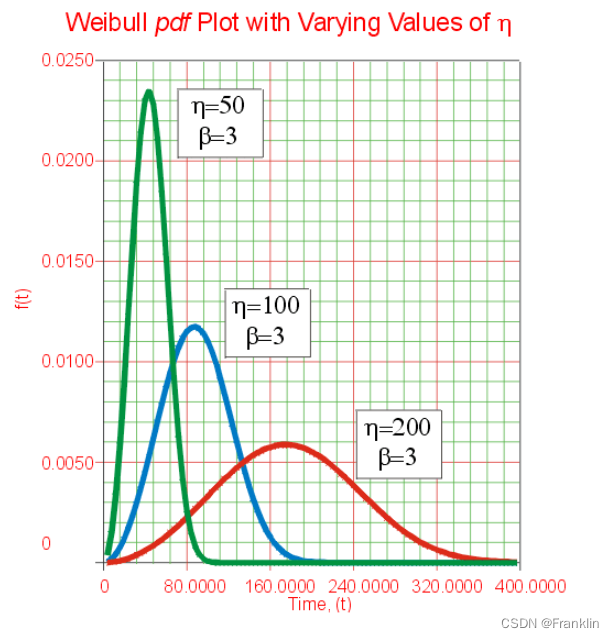
  It looks like this ：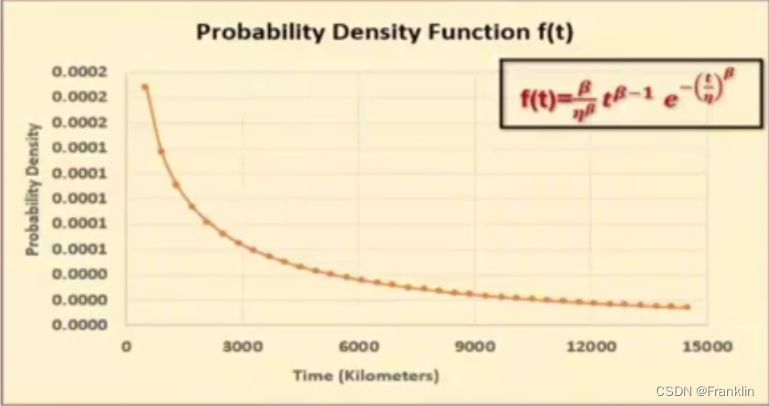
  

however , Actually, the more detailed definition of Weber distribution is 3 The expression of the parameter .

3.3 Three parameter Weber distribution Weibull Distribution Of PDF(Probability density function)

A continuous random variable X, The three parameter Weber distribution with the following three parameters and density function .

$$f(t;\beta ,\eta ,\gamma )=\{\begin{array}{ccc}\frac{\beta }{{\eta }^{\beta }}(t-\gamma {)}^{\beta -1}{e}^{-(\frac{t-\gamma }{\eta }{)}^{\beta }}& t,\beta ,\eta >0& \\ 0& ItsHelovecondition& \end{array}$$

• β (shape parameter shape parameter ) Also known as weibull slope Weber slope
• η (scale parameter Scaling parameters ）
• γ (location parameter Positional arguments , Also known as threshold Threshold parameters )
  【 case , so , When γ=0 When , A three parameter distribution becomes a two parameter distribution 】

3.4 Single parameter - standard Weibull Distribution Of PDF

【 Case extract , The Greek alphabet is a little different 】

4 Failure rate function (Hazard Rate or Failure rate Function)

$$h(t)=\frac{f(t)}{R(t)}=\frac{\frac{\beta }{{\eta }^{\beta }}{t}^{\beta -1}{e}^{-(\frac{t}{\eta }{)}^{\beta }}}{e^{-(\frac{t}{\eta }{)}^{\beta }}}=\frac{\beta }{{\eta }^{\beta }}.t^{\beta -1}$$

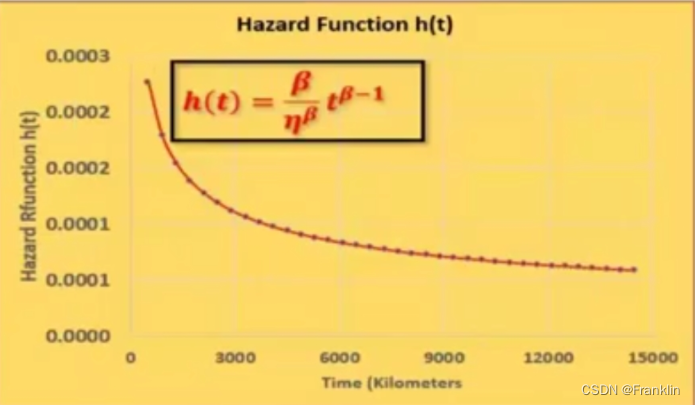
5 Mathematical expectation or life expectancy calculation ( Weibull mean life or MTTF)

【 Three parameter formula 】
$$E(X)=\eta \Gamma \left(1+\frac{1}{\beta }\right)+\mu$$
【 Two parameter formula 】
$$E(X)=\eta \Gamma \left(1+\frac{1}{\beta }\right)$$
$$\Gamma (x)$$【 case , Here comes the gamma function , There are more detailed descriptions in the reference list 】

6 Variance formula (Variance)

$$\sigma ={\eta }^2\left[\Gamma \left(1+\frac{2}{\beta }\right)-{\Gamma }^2\left(1+\frac{1}{\beta }\right)\right]$$

7 Other related definition formulas

7.1 skewness （skewness）

7.2 kurtosis （kurtosis）

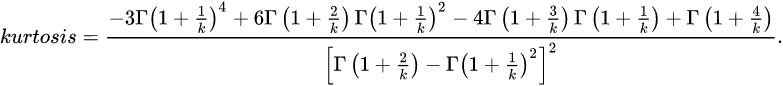
7.3 The median equation , Or call it B50 The formula

【 case , It is used to calculate the maintenance period of a car, for example 、 Or the calculation of intermediate maintenance of other systems 】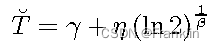

7 Noun reference ：

7.0 Cumulative distribution ：（Cumulative Density）CDF

Fx(x) = P(X ≤ x) [CDF It is all possible probabilities before accumulating random variables .【 case , Generally use large F(x) describe 】
【 case , A simple example , Throw dice , It's a random event 6 The probability of different results is the same , that , get 1 The probability of a point is 1/6, get 2 The probability of a point is also 1/6, that , get 2 Probability of the following points , Is to obtain 1 The sum of the probabilities of points 2 The sum of the probabilities of points , That is, cumulative probability , It can be expressed as less than or equal to 2 The probability of 1/6 + 1/6 = 2/6 = 1/3】
So there is ：

Probability of getting 1 = P(X≤ 1 ) = 1 / 6
Probability of getting 2 = P(X≤ 2 ) = 2 / 6
Probability of getting 3 = P(X≤ 3 ) = 3 / 6
Probability of getting 4 = P(X≤ 4 ) = 4 / 6
Probability of getting 5 = P(X≤ 5 ) = 5 / 6
Probability of getting 6 = P(X≤ 6 ) = 6 / 6 = 1

This is discrete ,

Where X is the probability that takes a value less than or equal to x and that lies in the semi-closed interval (a,b], where a < b.
P(a < X ≤ b) = Fx(b) – Fx(a)

If , Make it continuous , that ,CDF It can be seen as PDF Integral , The following example shows this relationship ：
It is known that PDF,

seek CDF,

7.1 Probability density ：（Probability Density）PDF

Probability density , General description , You can refer to the reference link at the end of the article . Here is a brief summary .
We understand probability density ,PD, It can be considered as the probability of a random event . then , The value of this probability p(x), It has a corresponding relationship with the random events , We can think of it as a function ,f(x).

x The definition domain of is understood as the definition interval related to probability , The probability of an event occurring at random . The probability of occurrence of events in all intervals is obviously 1.
Simply speaking, probability density has no practical significance , It must have a definite bounded interval . The probability density can be regarded as the ordinate , The interval is regarded as the abscissa , The integral of the probability density over the interval is the area , And this area is the probability of the event occurring in this interval , The sum of all areas is 1
For random variables X Distribution function of F(x), If there is a nonnegative integrable function f(x), So that for any real number x, Yes

be X Is a continuous random variable , call f(x) by X The probability density function of , Referred to as Probability density .
【 case , Generally use large F(x) describe CDF,f(x) describe PDF】

7.2 Gamma function

Gamma function can be seen everywhere in mathematics .
From Statistics , number theory , Complex analysis in mathematics , To string theory in physics . It seems to be a mathematical glue , Connect different areas .
1738 year , The great Euler , Aspire to extend factorial to non integer range .
$$\Gamma \left(n\right)=\left(n-1\right)!$$
【 For this derivation, please refer to the link at the end of the article , All in all , The gamma function can be expressed as the following expression from discrete to continuous 】
$$\Gamma \left(n\right)={\int }_0^{\infty }{t}^{n-1}{e}^{-t}dt$$

7.2.1 Properties of gamma function ：

7.2.2 Gamma distribution ：

7.2.3 Mathematical expectation and variance of gamma distribution

7.3 Mathematical expectation 【 mean value 】

7.3.1 Definition ：

Namely mean value ： In probability and Statistics , Mathematical expectation (mathematic expectation [4] )（ Or the average , Also called expectation ）
Is the probability of each possible result in the test multiplied by the sum of its results , Is one of the most basic mathematical characteristics . It reflects Average value of random variable Size .
expression ,E(x)

7.3.2 The story of origin ：

stay 17 century , A gambler challenged Pascal, a famous French mathematician , Gave him a title ： A and B gamble , The two of them have an equal chance of winning , The rule of the game is to win three games first , There are five games in total , The winner can get 100 The reward of francs . When the game reaches the fourth inning , A won two games , B won a game , At this time, for some reason, the game was suspended , So how to distribute this 100 Francs are fair ？
With the knowledge of probability theory , It's not hard to know , A is more likely to win , B has little chance of winning .
Because the possibility of a losing the last two games is only (1/2)×(1/2）=1/4, That is to say, the probability of a winning the last two games or any one of the last two games is 1－(1/4)=3/4, Jiayou 75% Expect to get 100 franc ; And B expects to win 100 Franc will have to beat a in both the last two games , The probability of B winning the last two games in a row is (1/2)(1/2)=1/4, That is, B has 25% Expect to get 100 Franc bonus .
so , Although we can't play any more , But based on the above possibilities , The objective expectations for the final victory of Party A and Party B are 75% and 25%, Therefore, a should share the bonus 10075%=75( franc ), B should get the bonus 100×25%=25( franc ). There's something in this story “ expect ” The word , Mathematical expectations come from this .

7.3.3 Continuous mathematical expectation

Let continuous random variable X The probability density function of is f(x), If integral converges absolutely , Then the value of the integral

Is the mathematical expectation of random variables , Write it down as E(X).

7.4 Gaussian distribution

Normal Probability Distribution Formula
$$\begin{array}{l}P(x)=\frac{1}{\sqrt{2\pi {\sigma }^2}}{e}^{-(x-\mu {)}^2/2{\sigma }^2}\end{array}$$
μ = Mean
σ = Standard Distribution.
x = Normal random variable.

Literature reference ：

Cumulative Distribution Function

Weibull Distribution , ASQ ,Hemant Urdhwareshe

Characteristics of the Weibull Distribution

The New Weibull Handbook

The most beautiful function in the world ——γ function , A pearl on the crown of mathematics
Understanding Probability Distributions