【GAN】《ENERGY-BASED GENERATIVE ADVERSARIAL NETWORKS》 ICLR‘17

《ENERGY-BASED GENERATIVE ADVERSARIAL NETWORKS》

Let's first introduce EBGAN, Read more about why you did this .

Auto-encoder Discriminator

Energy-based GAN And ordinary GAN The difference is that Discriminator The network architecture is changed from a binary classifier to a auto-encoder, And then use auto-encoder Of reconstruction error As the output of the discriminator . The model diagram is as follows

So the input of the discriminator is the same as that of the common GAN equally , It's still a picture , The output is also a scalar used to provide a gradient for the generator . So this AE How did you get it ？

In the picture Auto-encoder It is pre trained on a large number of real pictures , So when a real picture is entered AE when , The reconstruction error will be relatively small , When the image is generated for input, the reconstruction error will be large . In this way, we can naturally get EBGAN Of loss Function ：
$$\begin{array}{rl}{\mathcal{L}}_D(x,z)& =D(x)+[m-D(G(z)){]}^{+}\\ & =\Vert \mathrm{Dec}(\mathrm{Enc}(x))-x\Vert +[m-\Vert \mathrm{Dec}(\mathrm{Enc}(G(z)))-G(z)\Vert {]}^{+}\end{array}\text{\hspace{1em}(1)}$$

$$\begin{array}{rl}{\mathcal{L}}_G(z)& =\Vert D(G(z))\Vert \\ & =\Vert \mathrm{Dec}(\mathrm{Enc}(G(z)))-G(z)\Vert \end{array}\text{\hspace{1em}(2)}$$

among $[\cdot {]}^{+}=\max (0,\cdot )$,$D(\cdot )=\Vert \mathrm{Dec}(\mathrm{Enc}(\cdot ))-\cdot \Vert$,$m$ It's a margin, Then explain . Minimization formula （1） Means minimizing $D(x)$ And maximize $D(G(z))$, That is, the discriminator should score real pictures as low as possible , The score of generated pictures should be higher . But not too high , need margin.

margin

It is difficult to fit and approximate a thing in a neural network , But it's easy to destroy a thing , If we try to maximize the cost of reconstruction, it's easy , As long as you output a random noise to all the input pictures, you can get a very large $D(G(z))$, So we need to constrain an upper bound .

As shown in the figure below

When there's a margin Constraints , When the curve corresponding to the generated image is raised to a certain extent, there will be no penalty , At this time loss It mainly comes from lowering the curve of the real picture . That's it EGBAN Optimization process of .

Pulling-away Term

Pulling-away Term It is used to ensure the diversity of generation 、 solve mode collapse The problem of . The author first mentioned Salimans et al.,2016 Proposed “minibatch discriminator”, His thoughts are given every time D Enter a batch, and D To test the whole batch Instead of checking each picture separately .Real image batch Each picture in is different , And if it does mode collapse, That is, all pictures are the same , It must be false .

The author proposes here that pulling-away term, abbreviation PT：
$$f_{PT}(S)=\frac{1}{N(N-1)}\sum _i\sum _{j\ne i}{\left(\frac{S_i^{\top }{S}_j}{\Vert S_i\Vert \Vert S_j\Vert }\right)}^2\text{\hspace{1em}(3)}$$
The idea is generative fake image batch Each picture in the goes through D Of Encoder After encoding, a vector is generated , Two vectors calculate cosine Distance and sum to average . Making this term as small as possible means that the two vectors are closer to orthogonality , The generated image batch The greater the internal diversity . Note this is only for G Training when generating fake pictures .PT It also has weight , In the experiment, the author takes 0.1.

Energy-based

Now we know EBGAN 了 , there energy It means auto-encoder Output .Energy Function Namely AE,AE The output of is energy.Energy Function Will tend to give real pictures (high quality) Lower energy , Generate pictures (low quality) Higher energy . use MSE To represent energy is also more vivid , Entropy is the unit of energy , The minimum entropy is the minimum energy .AE Train on lots of real pictures , Has been able to simulate the distribution of real pictures , The generated picture goes through AE The entropy of the output is naturally larger .

use energy Not two 01 Values can also avoid GAN The problem of gradient disappearance , It can give different gradient values to different quality generated pictures .

Another angle

Borrow the article of sujianlin 《 From the perspective of energy GAN Model 》 Graph ：

At first the energy function is just a straight line .

Then the real sample $x_1,x_2,\dots x_n$ In turn $U(x)$ On , Extrude a bumpy function , Secure it ,$U(x)$ It forms an energy function .（EBGAN Inside Auto-encoder）

Next, we get a batch of generated samples ,$\widehat{x_1},\widehat{x_2},\dots \widehat{x_n}$, Put them anywhere in $U(x)$ On . And fix it $U(x)$, Release $\widehat{x_1},\widehat{x_2},\dots \widehat{x_n}$, therefore $\widehat{x_1},\widehat{x_2},\dots \widehat{x_n}$ Will follow “ energy ” The slope slowly rolled down to the bottom of the pit （ Fixed discriminator , Training generator ）, And the bottom of the pit represents the real sample , therefore $\widehat{x_1},\widehat{x_2},\dots \widehat{x_n}$ They all look like real samples .

And when training the generator , Because there are many “ pit ”, There are many options for optimization ：

For example, the generated sample in the above figure $\widehat{x_1}$ Slide slowly , Not necessarily $x_1$ The pit of , But just get to the middle one “ Secondary truth ” The pit of , So it needs to be improved 、 correct , Try to cross the barrier and slide to the lowest point .

Consider adding momentum to the optimization , As shown in the figure below ：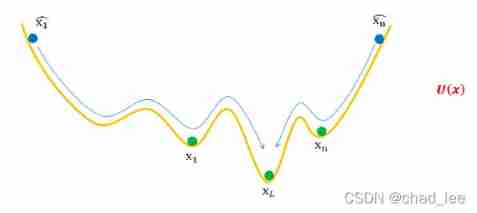

But this will lead to new problems ： False samples leaped across the nearest pit , To reach a very far but low pit , Gather near some real samples , And then there comes Mode Collapse problem ：

（ This may explain W-GAN Compare with GAN improvement ：“ Don't use momentum based optimization algorithms （ Include momentum and Adam）, recommend RMSProp,SGD It's OK ”）

This is also in the EBGAN Add Pulling-away Term Why .

advantage

EBGAN The discriminator can hardly require negative example training , Only a large number of real samples are needed to train the discriminator , Big advantage .

Energy models and anomalies API Sequence detection

I think this EBGAN And the previous exception API The core idea of sequence detection is very similar to , It can also be an energy model ：

• stay EBGAN in , The energy function is Auto-Encoder, Fitting training on a large number of real samples in advance , So we can give the real sample a lower entropy 、 False samples have higher entropy ; stay GAN During training, the entropy of real samples is continuously reduced 、 Properly increase the entropy of false samples .

• In anomaly detection , The energy function is “API Prediction module ”, In advance in a large number of normal API Prediction training on the sequence , So as to give normal API The lower entropy of the sequence 、 malice API The higher entropy of the sequence ; Keep decreasing the normal level during model training API Entropy on a sequence 、 Appropriately increase malicious API Entropy on a sequence （Unlearning）.

Include DeepLog、《Lifelong Anomaly Detection Through Unlearning》 Seems to fit into the energy model , It's just Energy Function Different forms .