Rolling Division

division

Don't talk much , The strongest code first ：

int gcd(int a, int b){
    
	return b == 0 ? a : gcd(b, a % b);
}

The return value of this function is a and b Maximum common divisor of

Introduction of rolling division

division algorithm You can find the greatest common divisor , seeing the name of a thing one thinks of its function , Divide repeatedly , Finally, we get the greatest common divisor of the two numbers .
First, let's analyze the theorem ：

Theorem ： The greatest common divisor of two integers is equal to the lesser one and the greatest common divisor of the remainder . greatest common divisor （Greatest Common Divisor） Abbreviation for GCD.
gcd(a,b) = gcd(b,a mod b) ( Might as well set a>b And r=a mod b ,r Not for 0)

Words are hard to understand , For example ：
134 / 18 = 7 … 8
18 / 8 = 2 … 2
8 / 2 = 4 … 0

See , Is it exactly the same as the theorem , So we need to find the greatest common divisor , and 134 /18 And 8 / 2 The greatest common divisor of is equal to , So we just need to find out 8 / 2 Maximum common divisor of , Is that what I said at the beginning? Change two numbers and then find , And we need to know , Because two numbers are divided , Remainder is 0, Its divisor must be the greatest common divisor , So here 2 That's what we're looking for 138 / 18 Maximum common divisor of . As for the proof , Baidu search , There are . The main proof idea is , Yes a/b more than r In the form of , To assume that y by a,b The common factor of , Prove again b,r The common divisor of is also y.

The last flow chart ：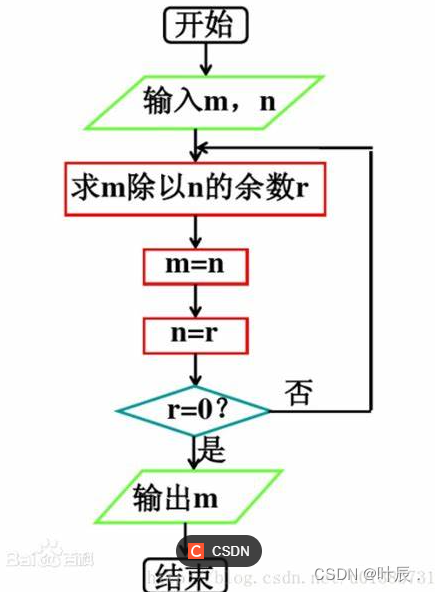

Code implementation ：

int gcd(int a,int b){
    
    int r=1;//  remainder , The initial value of the assignment is 1
    while(r!=0){
    //  If a<b, There is no need to reverse ab, Quotient in calculation 0 Codivisor itself , It can be reversed in the next operation 
        r = a % b;
        a = b;
        b = r;
    }
    return a;
}