【搜索】双向广搜 + A*

---

双向广搜

一般用于求解“最小步数”模型问题

双向广搜可以避免在深层子树上浪费时间。

在一些问题中，问题不但具有“初态”，还具有明确的“终态”，并且从初态开始搜索到终态开始逆向搜索产生的搜索树能够覆盖整个状态空间。

在这种条件下，可以采用双向广搜——从初态和终态出发各搜索一半状态，产生两棵深度减半的搜索树，在中间交会，组合成最终的答案。

---

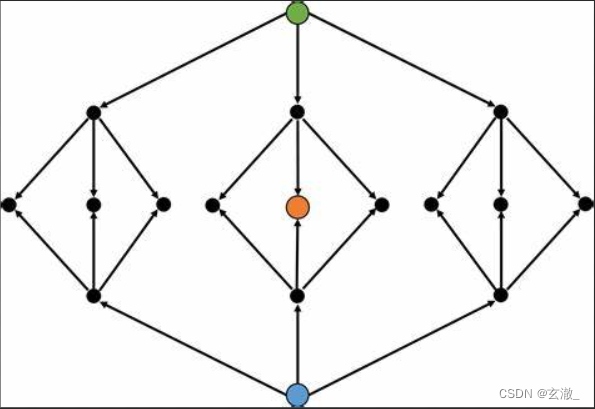
AcWing 190. 字串变换 （双向广搜）

 

输入样例：

abcd xyz
abc xu
ud y
y yz

输出样例：

3

---

 

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <unordered_map>

using namespace std;

const int N = 6;

int n;
string A, B;
string a[N], b[N];

int extend(queue<string>& q, unordered_map<string, int>&da, unordered_map<string, int>& db, 
    string a[N], string b[N])
{
    int d = da[q.front()];
    while (q.size() && da[q.front()] == d)
    {
        auto t = q.front();
        q.pop();

        for (int i = 0; i < n; i ++ )
            for (int j = 0; j < t.size(); j ++ )
                if (t.substr(j, a[i].size()) == a[i])
                {
                    string r = t.substr(0, j) + b[i] + t.substr(j + a[i].size());
                    if (db.count(r)) return da[t] + db[r] + 1;
                    if (da.count(r)) continue;
                    da[r] = da[t] + 1;
                    q.push(r);
                }
    }

    return 11;
}

int bfs()
{
    if (A == B) return 0;
    queue<string> qa, qb;
    unordered_map<string, int> da, db;

    qa.push(A), qb.push(B);
    da[A] = db[B] = 0;

    int step = 0;
    while (qa.size() && qb.size())
    {
        int t;
        if (qa.size() < qb.size()) t = extend(qa, da, db, a, b);
        else t = extend(qb, db, da, b, a);

        if (t <= 10) return t;
        if ( ++ step == 10) return -1;
    }

    return -1;
}

int main()
{
    cin >> A >> B;
    while (cin >> a[n] >> b[n]) n ++ ;

    int t = bfs();
    if (t == -1) puts("NO ANSWER!");
    else cout << t << endl;

    return 0;
}

---

A* 

关于优先队列BFS算法，该算法维护了一个优先队列（二叉堆），不断从堆中取出“当前代价最小”的状态（堆顶）进行扩展。每个状态第一次从堆中取出时，就得到了从初态到该状态的最小代价。

如果给定一个“目标状态”，需要求出从初态到目标状态的最小代价，你们优先队列BFS这个“优先策略”是不够完善的。一个状态的当前代价最小，只能说明从起点到该状态的代价很小，而在未来的搜索中，从该状态到目标状态可能会花费很大的代价。另外，一些状态虽然当前的代价略大，但是未来到目标状态的代价可能很小，于是从起始状态到目标状态的总代价反而更优。

优先队列BFS优先选择前者的分支，导致求出最优解的搜索量增大。为了提高效率，可以对未来可能产生的代价进行预估。

我们可以设计一个“估价函数”，以“任意状态”为输入，计算从该状态到目标状态所需代价的估计值。在搜索中，仍需维护一个堆，不断从堆中取出“当前代价+未来估价”最小的状态进行拓展。

为了保证第一次从堆中取出目标状态时得到的就是最优解，我们设计的估价函数需要满足一个基本准则

设当前状态 state 到目标状态所需的估计值是 f(state)

设在未来的搜索中，实际求出从当前的状态 state 到目标状态的最小代价是 g(state)

对于任意的 state ，应该有 

也就是说，估价函数的估值不能大于未来实际代价，估价比实际代价更优

---

AcWing 179. 八数码

 

输入样例：

2  3  4  1  5  x  7  6  8 

输出样例

ullddrurdllurdruldr

---

估价函数：当前状态中每个数和它的目标位置的曼哈顿距离之和

---

#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>
#include <unordered_map>

using namespace std;

int f(string state)
{
    int res = 0;
    for (int i = 0; i < state.size(); i ++ )
        if (state[i] != 'x')
        {
            int t = state[i] - '1';
            res += abs(i / 3 - t / 3) + abs(i % 3 - t % 3);
        }
    return res;
}

string bfs(string start)
{
    int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
    char op[4] = {'u', 'r', 'd', 'l'};

    string end = "12345678x";
    unordered_map<string, int> dist;
    unordered_map<string, pair<string, char>> prev;
    priority_queue<pair<int, string>, vector<pair<int, string>>, greater<pair<int, string>>> heap;

    heap.push({f(start), start});
    dist[start] = 0;

    while (heap.size())
    {
        auto t = heap.top();
        heap.pop();

        string state = t.second;

        if (state == end) break;

        int step = dist[state];
        int x, y;
        for (int i = 0; i < state.size(); i ++ )
            if (state[i] == 'x')
            {
                x = i / 3, y = i % 3;
                break;
            }
        string source = state;
        for (int i = 0; i < 4; i ++ )
        {
            int a = x + dx[i], b = y + dy[i];
            if (a >= 0 && a < 3 && b >= 0 && b < 3)
            {
                swap(state[x * 3 + y], state[a * 3 + b]);
                if (!dist.count(state) || dist[state] > step + 1)
                {
                    dist[state] = step + 1;
                    prev[state] = {source, op[i]};
                    heap.push({dist[state] + f(state), state});
                }
                swap(state[x * 3 + y], state[a * 3 + b]);
            }
        }
    }

    string res;
    while (end != start)
    {
        res += prev[end].second;
        end = prev[end].first;
    }
    reverse(res.begin(), res.end());
    return res;
}

int main()
{
    string g, c, seq;
    while (cin >> c)
    {
        g += c;
        if (c != "x") seq += c;
    }

    int t = 0;
    for (int i = 0; i < seq.size(); i ++ )
        for (int j = i + 1; j < seq.size(); j ++ )
            if (seq[i] > seq[j])
                t ++ ;

    if (t % 2) puts("unsolvable");
    else cout << bfs(g) << endl;

    return 0;
}

---

AcWing 178. 第K短路 

 

 

输入样例：

2 2
1 2 5
2 1 4
1 2 2

输出样例：

14

---

采用Dijkstra最短路思想，每次扩展最短的路径，第 k 次到达终点时的路径长度即为第 k 短路的长度。

由于算法相当于同时进行 k 次单元最短路，时间和空间都可能会超限，因此 预处理每个点到终点的最短距离作为估价函数，利用 A∗算法优化。

复杂度为

---

#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>

#define x first
#define y second

using namespace std;

typedef pair<int, int> PII;
typedef pair<int, PII> PIII;

const int N = 1010, M = 200010;

int n, m, S, T, K;
int h[N], rh[N], e[M], w[M], ne[M], idx;
int dist[N], cnt[N];
bool st[N];

void add(int h[], int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}

void dijkstra()
{
    priority_queue<PII, vector<PII>, greater<PII>> heap;
    heap.push({0, T});

    memset(dist, 0x3f, sizeof dist);
    dist[T] = 0;

    while (heap.size())
    {
        auto t = heap.top();
        heap.pop();

        int ver = t.y;
        if (st[ver]) continue;
        st[ver] = true;

        for (int i = rh[ver]; ~i; i = ne[i])
        {
            int j = e[i];
            if (dist[j] > dist[ver] + w[i])
            {
                dist[j] = dist[ver] + w[i];
                heap.push({dist[j], j});
            }
        }
    }
}

int astar()
{
    priority_queue<PIII, vector<PIII>, greater<PIII>> heap;
    heap.push({dist[S], {0, S}});

    while (heap.size())
    {
        auto t = heap.top();
        heap.pop();

        int ver = t.y.y, distance = t.y.x;
        cnt[ver] ++ ;
        if (cnt[T] == K) return distance;

        for (int i = h[ver]; ~i; i = ne[i])
        {
            int j = e[i];
            if (cnt[j] < K)
                heap.push({distance + w[i] + dist[j], {distance + w[i], j}});
        }
    }

    return -1;
}

int main()
{
    scanf("%d%d", &n, &m);
    memset(h, -1, sizeof h);
    memset(rh, -1, sizeof rh);

    for (int i = 0; i < m; i ++ )
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(h, a, b, c);
        add(rh, b, a, c);
    }
    scanf("%d%d%d", &S, &T, &K);
    if (S == T) K ++ ;

    dijkstra();
    printf("%d\n", astar());

    return 0;
}