当前位置:网站首页>NDT registration principle
NDT registration principle
2022-06-12 12:13:00 【xinxiangwangzhi_】
List of articles
summary :NDT It is a point cloud registration method of probability model . be relative to icp for : It has a wide range of convergence , Insensitive to initial value . Speed and other advantages . But the precision is not icp high .
NDT Preliminary knowledge
Normal distribution
n Dimensional normal random process , The probability density function is :
p ( x ⃗ ) = 1 ( 2 π ) D / 2 ∣ Σ ∣ exp ( − ( x ⃗ − μ ⃗ ) T Σ − 1 ( x ⃗ − μ ⃗ ) 2 ) (1) p(\vec{x})=\frac{1}{(2 \pi)^{D / 2} \sqrt{|\boldsymbol{\Sigma}|}} \exp \left(-\frac{(\vec{x}-\vec{\mu})^{\mathrm{T}} \boldsymbol{\Sigma}^{-1}(\vec{x}-\vec{\mu})}{2}\right)\tag{1} p(x)=(2π)D/2∣Σ∣1exp(−2(x−μ)TΣ−1(x−μ))(1)
among μ ⃗ , Σ \vec{\mu},\Sigma μ,Σ Means mean , And covariance matrix , The calculation is as follows :
μ ⃗ = 1 m ∑ k = 1 m y ⃗ k (2) \vec{\mu}=\frac{1}{m} \sum_{k=1}^{m} \vec{y}_{k}\tag{2} μ=m1k=1∑myk(2)
Σ = 1 m − 1 ∑ k = 1 m ( y ⃗ k − μ ⃗ ) ( y ⃗ k − μ ⃗ ) T (3) \Sigma =\frac{1}{m-1} \sum_{k=1}^{m}\left(\vec{y}_{k}-\vec{\mu}\right)\left(\vec{y}_{k}-\vec{\mu}\right)^{\mathrm{T}}\tag{3} Σ=m−11k=1∑m(yk−μ)(yk−μ)T(3)
Gauss Newton method for solving nonlinear least squares
I will write a blog afterwards
NDT principle
(1) Objective function
NDT Full name : normal distributions transform, Normal distribution transformation , It can be described as a kind of compact ( concise ) A method of representing a surface .
This transform maps the point cloud to a smooth surface representation , Described as a set of local probability density functions (PDF), Each of these functions describes the shape of a partial surface . The local probability density function is used to represent the local point cloud .
When using NDT When performing scanning registration , By maximizing the position of the current point to be registered in the reference ( The benchmark ) Possibility of scanning the surface , So as to find the current posture of the point cloud to be registered . That is to maximize the following likelihood function :
Ψ = ∏ k = 1 n p ( T ( p ⃗ , x ⃗ k ) ) (4) \Psi=\prod_{k=1}^{n} p\left(T\left(\vec{p}, \vec{x}_{k}\right)\right)\tag{4} Ψ=k=1∏np(T(p,xk))(4)
p ⃗ , x ⃗ k , p ( x ⃗ ) \vec{p},\vec{x}_{k},p(\vec{x}) p,xk,p(x) Namely : Transformation matrix corresponding to attitude , Point cloud to be registered , The probability density function of the reference point cloud corresponding to the point cloud to be registered .PDF The probability density function is not necessarily a normal distribution , Able to describe local surfaces , And the probability density functions that are robust to outliers are all OK .
The maximization formula (4) Equivalent to minimization formula (5):
− log Ψ = − ∑ k = 1 n log ( p ( T ( p ⃗ , x ⃗ k ) ) ) (5) -\log \Psi=-\sum_{k=1}^{n} \log \left(p\left(T\left(\vec{p}, \vec{x}_{k}\right)\right)\right)\tag{5} −logΨ=−k=1∑nlog(p(T(p,xk)))(5)
(2) Simplify the objective function

left (a) It's a normal distribution ( Red ) And mixed distribution p ˉ ( x ⃗ ) \bar{p}(\vec{x}) pˉ(x)( normal 、 Uniform distribution , green ) Image , On the right side (b) For the corresponding -log logarithm . from (b) In the clear , The original normal distribution is relative to x There is no constraint , stay x The value of the function will also be greatly affected when the value of becomes larger , And the hybrid model will be right x The value of , Better robustness .( Less affected by noise points )
To observe the above (b) The red curve of − l o g ( p ( x ) ) -log(p(x)) −log(p(x)), Its extreme value is found to be positive infinity . To avoid extremes x Value causes y The value is infinite or infinitesimal , And avoid the influence of outliers , The normal probability density function (1) Change to the mixed distribution formula of normal distribution and uniform distribution (6):
p ˉ ( x ⃗ ) = c 1 exp ( − ( x ⃗ − μ ⃗ ) T Σ − 1 ( x ⃗ − μ ⃗ ) 2 ) + c 2 p o (6) \bar{p}(\vec{x})=c_{1} \exp \left(-\frac{(\vec{x}-\vec{\mu})^{\mathrm{T}} \Sigma^{-1}(\vec{x}-\vec{\mu})}{2}\right)+c_{2} p_{o}\tag{6} pˉ(x)=c1exp(−2(x−μ)TΣ−1(x−μ))+c2po(6)
p o p_{o} po Is the ratio of outliers , constant c1 and c2 You can integrate the probability density function to be equal to 1 To make sure .
The probability density function formula (1) Approximate formula (6) after , The target function − log ( p ˉ ( x ⃗ ) ) -\log({\bar{p}(\vec{x})}) −log(pˉ(x)) The first and second derivatives of are complex , therefore , Then put the formula (6) Convert to Gaussian form for approximation :
p ~ ( x ⃗ k ) = − d 1 exp ( − d 2 2 ( x ⃗ k − μ ⃗ k ) T Σ k − 1 ( x ⃗ k − μ ⃗ k ) ) (7) \tilde{p}\left(\vec{x}_{k}\right)=-d_{1} \exp \left(-\frac{d_{2}}{2}\left(\vec{x}_{k}-\vec{\mu}_{k}\right)^{\mathrm{T}} \boldsymbol{\Sigma}_{k}^{-1}\left(\vec{x}_{k}-\vec{\mu}_{k}\right)\right)\tag{7} p~(xk)=−d1exp(−2d2(xk−μk)TΣk−1(xk−μk))(7)
among :
d 3 = − log ( c 2 ) d 1 = − log ( c 1 + c 2 ) − d 3 d 2 = − 2 log ( ( − log ( c 1 exp ( − 1 / 2 ) + c 2 ) − d 3 ) / d 1 ) (8) \begin{aligned} &d_{3}=-\log \left(c_{2}\right) \\ &d_{1}=-\log \left(c_{1}+c_{2}\right)-d_{3} \\ &d_{2}=-2 \log \left(\left(-\log \left(c_{1} \exp (-1 / 2)+c_{2}\right)-d_{3}\right) / d_{1}\right)\tag{8} \end{aligned} d3=−log(c2)d1=−log(c1+c2)−d3d2=−2log((−log(c1exp(−1/2)+c2)−d3)/d1)(8)
The formula (7) omitted d3, Because it's a constant offset , The shape of its probability density function or the optimized parameters will not be changed .
Sum up , Given a series of point clouds X = { x ⃗ 1 , … , x ⃗ n } \mathcal{X}=\left\{\vec{x}_{1}, \ldots, \vec{x}_{n}\right\} X={ x1,…,xn}, Posture p ⃗ \vec{p} p, Transformation matrix T ( p ⃗ , x ⃗ ) T(\vec{p}, \vec{x}) T(p,x), the NDT score function s ( p ⃗ ) s(\vec{p}) s(p) It can be expressed as :
s ( p ⃗ ) = − ∑ k = 1 n p ~ ( T ( p ⃗ , x ⃗ k ) ) (9) s(\vec{p})=-\sum_{k=1}^{n} \tilde{p}\left(T\left(\vec{p}, \vec{x}_{k}\right)\right) \tag{9} s(p)=−k=1∑np~(T(p,xk))(9)
score function Defined as log likelihood First order derivation of See know . That's the formula 9 It's the formula 5 First derivative of .
(3) Numerical solution
The probability density function requires the inverse of the covariance , Because for linear 、 For flat point clouds , Covariance is singular , And irreversible . In addition to 3D In the space , When the number of point clouds is less than 3, Matrices are also singular , Covariance matrix is irreversible . Therefore, the maximum eigenvalue is assumed , The next largest eigenvalue , The minimum eigenvalues are respectively : λ 3 λ 2 λ 1 \lambda_{3}\lambda_{2}\lambda_{1} λ3λ2λ1, When λ 3 \lambda_{3} λ3 Greater than 100 Times λ 2 or person λ 1 \lambda_{2} perhaps \lambda_{1} λ2 or person λ1 when , Make λ 1 , 2 ′ = λ 3 / 100 \lambda_{1,2}^{\prime}=\lambda_{3} / 100 λ1,2′=λ3/100. New covariance matrix Σ ′ = V Λ ′ V \boldsymbol{\Sigma}^{\prime}=\mathbf{V} \Lambda^{\prime} \mathbf{V} Σ′=VΛ′V Replace the original covariance matrix Σ \boldsymbol{\Sigma} Σ, V \mathbf{V} V Is the matrix corresponding to the eigenvector Σ \boldsymbol{\Sigma} Σ :
Λ ′ = [ λ 1 ′ 0 0 0 λ 2 ′ 0 0 0 λ 3 ] (11) \Lambda^{\prime}=\left[\begin{array}{ccc} \lambda_{1}^{\prime} & 0 & 0 \\ 0 & \lambda_{2}^{\prime} & 0 \\ 0 & 0 & \lambda_{3} \end{array}\right]\tag{11} Λ′=⎣⎡λ1′000λ2′000λ3⎦⎤(11)
Using Newton's method , By optimizing the s ( p ⃗ ) s(\vec{p}) s(p), Can find Attitude parameters p ⃗ \vec{p} p .
Newton’s method iteratively solves the equation H Δ p ⃗ = − g ⃗ \mathrm{H} \Delta \vec{p}=-\vec{g} HΔp=−g, where H \mathrm{H} H and g ⃗ \vec{g} gare the Hessian matrix and gradient vector of s ( p ⃗ ) s(\vec{p}) s(p). The gradient can be expressed as :
g i = δ s δ p i = ∑ k = 1 n d 1 d 2 x ⃗ k ′ T Σ k − 1 δ x ⃗ k ′ δ p i exp ( − d 2 2 x ⃗ k ′ T Σ k − 1 x ⃗ k ′ ) (11) g_{i}=\frac{\delta s}{\delta p_{i}}=\sum_{k=1}^{n} d_{1} d_{2} \vec{x}_{k}^{\prime \mathrm{T}} \Sigma_{k}^{-1} \frac{\delta \vec{x}_{k}^{\prime}}{\delta p_{i}} \exp \left(\frac{-d_{2}}{2} \vec{x}_{k}^{\prime \mathrm{T}} \Sigma_{k}^{-1} \vec{x}_{k}^{\prime}\right)\tag{11} gi=δpiδs=k=1∑nd1d2xk′TΣk−1δpiδxk′exp(2−d2xk′TΣk−1xk′)(11)
The Hessian matrix is :
H i j = δ 2 s δ p i δ p j = ∑ k = 1 n d 1 d 2 exp ( − d 2 2 x ⃗ k ′ T Σ k − 1 x ⃗ k ′ ) ( − d 2 ( x ⃗ k ′ T Σ k − 1 δ x ⃗ k ′ δ p i ) ( x ⃗ k ′ T Σ k − 1 δ x ⃗ k ′ δ p j ) + x ⃗ k T Σ k − 1 δ 2 x ⃗ k ′ δ p i δ p j + δ x ⃗ k ′ δ p j Σ k − 1 δ x ⃗ k ′ δ p i ) (12) H_{i j}=\frac{\delta^{2} s}{\delta p_{i} \delta p_{j}}= \sum_{k=1}^{n} d_{1} d_{2} \exp \left(\frac{-d_{2}}{2} \vec{x}_{k}^{\prime}{ }^{\mathrm{T}} \boldsymbol{\Sigma}_{k}^{-1} \vec{x}_{k}^{\prime}\right)\left(-d_{2}\left(\vec{x}_{k}^{\prime}{ }^{\mathrm{T}} \boldsymbol{\Sigma}_{k}^{-1} \frac{\delta \vec{x}_{k}^{\prime}}{\delta p_{i}}\right)\left(\vec{x}_{k}^{\prime}{ }^{\mathrm{T}} \boldsymbol{\Sigma}_{k}^{-1} \frac{\delta \vec{x}_{k}^{\prime}}{\delta p_{j}}\right)+\\ \vec{x}_{k}^{\mathrm{T}} \boldsymbol{\Sigma}_{k}^{-1} \frac{\delta^{2} \vec{x}_{k}^{\prime}}{\delta p_{i} \delta p_{j}}+\frac{\delta \vec{x}_{k}^{\prime}}{\delta p_{j}} \boldsymbol{\Sigma}_{k}^{-1} \frac{\delta \vec{x}_{k}^{\prime}}{\delta p_{i}}\right)\tag{12} Hij=δpiδpjδ2s=k=1∑nd1d2exp(2−d2xk′TΣk−1xk′)(−d2(xk′TΣk−1δpiδxk′)(xk′TΣk−1δpjδxk′)+xkTΣk−1δpiδpjδ2xk′+δpjδxk′Σk−1δpiδxk′)(12)
2D,3D NDT The gradient and Heissian The matrix form is the same , The difference is that the transformation matrix T( See the original text for the formula , There is no formula posted here ).2D 3D NDT The difference between them mainly lies in the transformation matrix , And the transformation matrix is different from the first-order and second-order matrix .
(4) Algorithm flow :
The algorithm flow is as follows :( Be careful Register scan : Point cloud to be registered (source), reference scan: Base point cloud (target))![[ Failed to transfer the external chain picture , The origin station may have anti-theft chain mechanism , It is suggested to save the pictures and upload them directly (img-51cSItJc-1653804976551)(./%E7%AE%97%E6%B3%95%E6%B5%81%E7%A8%8B.png)]](/img/00/cb60c088963bb508e71d12fbb4efca.png)
(5) comparison ICP The advantages of
NDT Class method ratio ICP This kind of algorithm has higher efficiency and wider convergence region , about 2D and 3D The application has a relatively mature solution , But in the absence of a good initial value , It will also fall into local optimization .
- Insensitive to initial value ( The initial value is also required )
- No nearest neighbor search is required , Fast
NDT stay PCL application
#pragma once
/* * @Description: Registration using normal distribution transformation * https://www.cnblogs.com/li-yao7758258/p/6554582.html * http://robot.czxy.com/docs/pcl/chapter03/registration/#ndt * @Author: HCQ * @Company(School): UCAS * @Email: [email protected] * @Date: 2020-10-22 19:20:43 * @LastEditTime: 2020-10-22 19:26:04 * @FilePath: /pcl-learning/14registration Registration /4 Normal distribution transformation registration (NDT)/normal_distributions_transform.cpp */
/* The experiment of registration using normal distribution transformation . among room_scan1.pcd room_scan2.pcd These point clouds contain the same room 360 Scanning data from different perspectives */
#include <iostream>
#include <pcl/point_types.h>
#include <pcl/registration/ndt.h> //NDT( Normal distribution ) Register class header file
int ndt(const pcl::PointCloud<pcl::PointXYZ>::Ptr cloud_source,
const pcl::PointCloud<pcl::PointXYZ>::Ptr cloud_target,
pcl::PointCloud<pcl::PointXYZ>::Ptr transformed_source)
{
// Initialize normal distribution (NDT) object
pcl::NormalDistributionsTransform<pcl::PointXYZ, pcl::PointXYZ> ndt;
// Set according to the scale of the input data NDT Related parameters
ndt.setTransformationEpsilon(0.03); // Set the minimum conversion difference for the termination condition
ndt.setStepSize(0.1); // by more-thuente Set the maximum step size for line search
ndt.setResolution(2.0); // Set up NDT The resolution of the mesh structure (voxelgridcovariance)
// Adding the maximum number of iterations limit can increase the robustness of the program and prevent it from running too long in the wrong direction
//ndt.setMaximumIterations(50);
ndt.setInputSource(cloud_source); // Source point cloud
// Setting point cloud to be aligned to.
ndt.setInputTarget(cloud_target); // Target point cloud
// Use the unit matrix as the initial value of the matrix
ndt.align( *transformed_source);
// This place output_cloud It cannot be used as the final source cloud transformation , Because the point cloud is filtered
std::cout << "Normal Distributions Transform has converged:" << ndt.hasConverged()
<< " score: " << ndt.getFitnessScore() << std::endl;
std::cout << "tf matrix:\n" << ndt.getFinalTransformation() << std::endl;
// Transform the filtered input point cloud using the transform you created
pcl::transformPointCloud(*cloud_source, *transformed_source, ndt.getFinalTransformation());
// Save the converted source cloud as the final transformation output
//pcl::io::savePCDFileASCII(transformed_source_name, *output_cloud);
return 0;
}
NDT The source code parsing
To be changed
Reference material
3d ndt The original paper 《Scan registration for autonomous mining vehicles using 3D-NDT》
3d ndt Doctoral Dissertation ( A more detailed )《The Three-Dimensional Normal-Distributions Transform — an Efficient Representation for Registration, Surface Analysis, and Loop Detection》
ndt And icp Compare 《 A survey of laser scanning matching methods 》
https://zhuanlan.zhihu.com/p/96908474
https://www.modb.pro/db/101593
https://www.codetd.com/en/article/13213393
边栏推荐
- Difference between Definition and Declaration
- win7注册进程外组件, 服务, 以及COM组件调试
- 【Leetcode】221. Largest Square
- 获取本机所有ipv4, ipv6地址
- LeetCode 1037. Effective boomerang (vector cross product)
- Batch load/store instructions of arm instruction set
- LeetCode_字符串_简单_344.反转字符串
- promise的理解已经利用promise实现图片的预加载(顺序加载)
- Find the median of two ordered arrays (leetcode 4)
- Beyondcompare 4 uses PJ
猜你喜欢
![[foundation of deep learning] back propagation method (1)](/img/0b/540c1f94712a381cae4d30ed624778.png)
[foundation of deep learning] back propagation method (1)

Cookie和Session

5G NR協議學習--TS38.211下行通道

Batch load/store instructions of arm instruction set

TinyMCE series (II) TinyMCE plug-in development
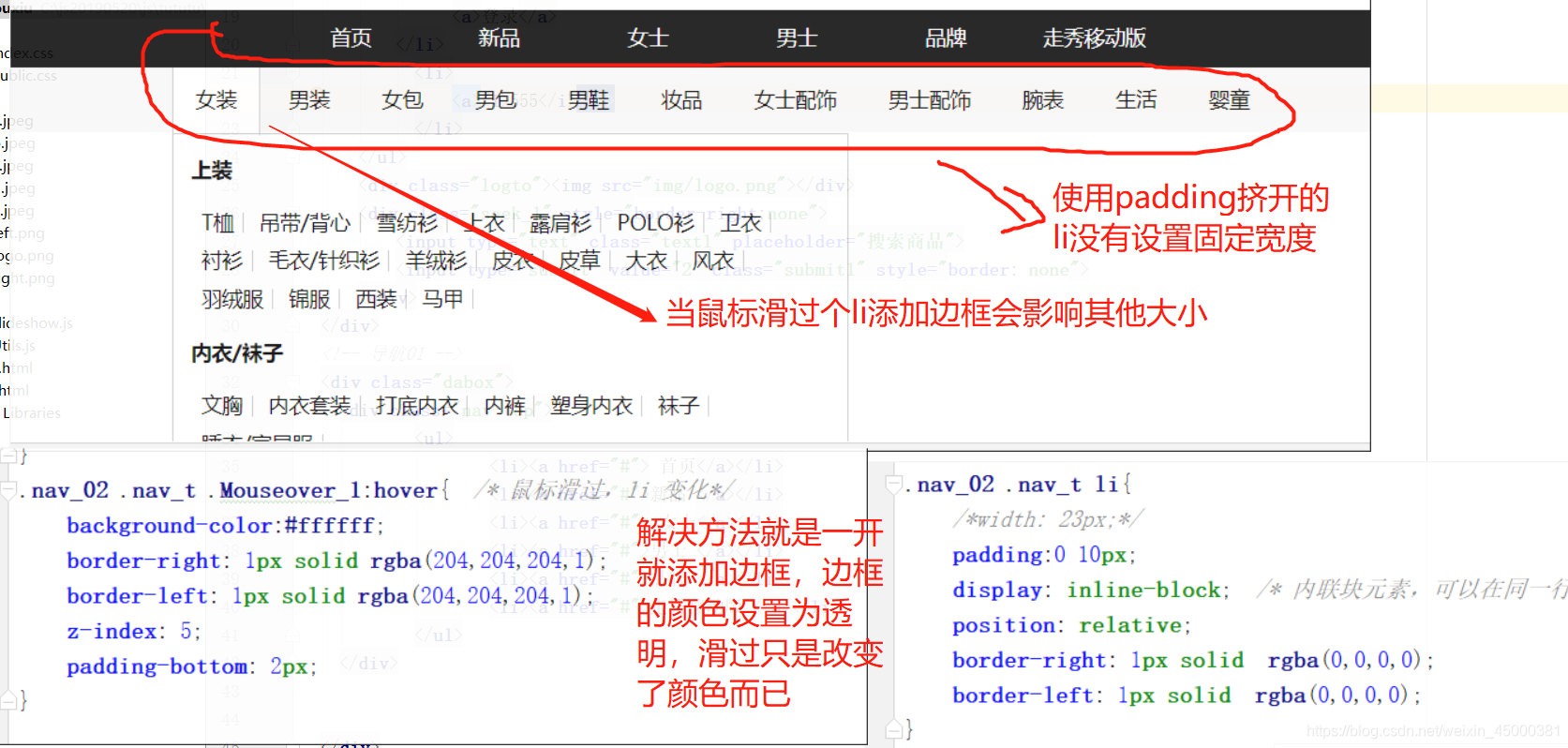
In navigation, the solution of adding borders to affect the layout

Common debugging tools and commands for ROS

LeetCode 1037. Effective boomerang (vector cross product)

转载--win10打开任务管理器就蓝屏的问题

mysql复习
随机推荐
Channel shuffle class
Google Earth engine (GEE) - quick land classification by kmeans clustering (double for loop quick parameter adjustment)
MySQL review
QT adds a summary of the problems encountered in the QObject class (you want to use signals and slots) and solves them in person. Error: undefined reference to `vtable for xxxxx (your class name)‘
TinyMCE series (I) TinyMCE environment construction
屏蔽不显示VS警告warning
What is modularity? Benefits of modularity
Basic concepts of machine learning
PDSCH related
第六章 数据类型(五)
ELK搭建指南
Difference between Definition and Declaration
[译] Go语言测试进阶版建议与技巧
Performance comparison test of channel and condition variables of golang in single production and single consumption scenarios
Why is there no traffic after the launch of new products? How should new products be released?
A. Prefix range
Implementation principle of kotlin extension function
Thirty one items that affect the weight of the store. Come and see if you've been hit
NDT配准原理
PDSCH 相关