当前位置:网站首页>网络流详解(流网图一般能够反映什么信息)
网络流详解(流网图一般能够反映什么信息)
2022-08-02 12:29:00 【全栈程序员站长】
大家好,又见面了,我是你们的朋友全栈君。
network-flows,网络流,传说中的省选算法
先推荐一个讲网络流思路的blog:
https://www.cnblogs.com/ZJUT-jiangnan/p/3632525.html
网络流有两种写法,dinic和sap(isap) 本人太弱了,只会dinic
目的
首先,明确网络流是干什么的
给定指定的一个有向图,其中有两个特殊的点源S(Sources)和汇T(Sinks),每条边有指定的容量(Capacity),求满足条件的从S到T的最大流(MaxFlow).
下面给出一个通俗点的解释
好比你家是汇 自来水厂是源
然后自来水厂和你家之间修了很多条水管子接在一起 水管子规格不一 有的容量大 有的容量小
然后问自来水厂开闸放水 你家收到水的最大流量是多少
如果自来水厂停水了 你家那的流量就是0 当然不是最大的流量 但是你给自来水厂交了100w美金 自来水厂拼命水管里通水 但是你家的流量也就那么多不变了 这时就达到了最大流
理解起来还好吧,也就是上文说的那样
实现
现在知道了到底要求什么了,但是怎么求?
先给个模型如下
首先来手算一下,很容易可以得出这个最大流是走(1,2,4)和(1,3,4)得到的2,即最大流为2
然后对于程序,我们先引入一个叫做残量图的概念
顾名思义,残嘛,就是剩的意思,即剩下的量,我们把一条边的最大容量MAXV和其实际的流量F的差值叫做残量,即
残量= M A X V − F MAXV – F MAXV−F
然后我们将残量作为每一条边的权值,构建一个图就叫做残量图,若权值为0,那么就相当于一条断边
此时,假设我们从源出发进行的某一次dfs到了汇,那么就说明这条路线的流量还可以增加,具体增加的量就被这条路线上的流量最小的那条边决定了,我们把这样的路叫做增广路
就像上图,我们知道(1,2,3,4)这条路线是可以在增大流量的,且最大可增大的流量是1,故我们就将其经过的边的残量-1得到了这个图
然后我们再dfs,却发现不能到达汇了,于是程序这个时候就返回此时的最大流,1
但是并不是这样的啊??
这个时候我们发现,如果程序在dfs到2的时候若可以向4dfs的话就不会出错了啊!那么这个时候,如果我们给这个图上的每一个点都标上深度的话,我们dfs的时候只允许从低深度往高深度走的话,岂不是可以大幅度避免出错呢?于是这个时候dinic算法的思想就出来了,就是不断用bfs标深度然后不断dfs直到不能到达汇为止
但是仅仅通过标记深度能不能完全解决问题呢?答案是不能的,即使它可以大幅度减少
那如果说我们可以让程序在dfs到3的时候发现问题并后悔不就ok了吗?
如果想要达到这种境界,我们可以写一个人工智能的学习算法,但是注意了,这是竞赛,是来搞笑的不是来毁灭人类的哈哈哈哈
于是有一种最easy的方法就是引入一个反向边的概念(怎么引入这么多概念),即每一条边(u,v)都有一条反向边(v,u),且这两条边的最大容量相等,实际流量之和等于最大流量,即
M A X V ( u , v ) = M A X V ( v , u ) MAXV(u,v)=MAXV(v,u) MAXV(u,v)=MAXV(v,u)
F ( u , v ) = F ( v , u ) = M A X V ( v , u ) = M A X V ( u , v ) F(u,v)=F(v,u)=MAXV(v,u)=MAXV(u,v) F(u,v)=F(v,u)=MAXV(v,u)=MAXV(u,v)
由于定义,当一条边的流量+或-a时,其反向边的流量-或+a
我们若引入反向边的概念后,就有了这样一个图
然后根据dfs,我们找到了增广路(1,2,3,4),然后图就该变成这样
然后我们继续dfs,把反向边也当作可走的边dfs,然后得到了增广路(1,3,2,4)
然后图就成了这样
最大流为2
仔细观察可以发现,上图其实和我们直接dfs(1,2,4)和(1,3,4)得到的结果一样!!这也就正确了!!
但是为什么可以正确呢?程序并没有大叫一声“啊,不该这样走!”
其实奥妙在第2个dfs
当程序将边(3,2)的流量加一,(2,3)的流量减一时,其实就相当于把边(2,3)的流量给退回去了(不信你看退回后的(2,3)和原图的(2,3)是不是一样的),然后还把本来属于路径(1,2,3,4)的流量“交付”给了(1,3),于是就有了两条路(1,2,4)和(1,3,4)
这就是其奥妙所在
于是这个算法框架就此浮出水面:
先标深度再用dfs找一次增广路然后再bfs标深度在dfs然后bfs,dfs,bfs,dfs,bfs,dfs,bfs,dfs…直到bfs时发现断层,说明此时已经找到了最大流
下面给个代码吧,有些细节还需要看看
题目来源:luoguP1343
//dinic
#include<bits/stdc++.h>
using namespace std;
#define INF INT_MAX
const int maxn=200+5;
const int maxm=2000+5;
int n,m,x,cnt=0;
int head[maxn];
int dis[maxn];
struct node
{
int e;
int v;
int nxt;
}edge[maxm<<1];
//**********************************function
inline int read(){
int ans=0;char r=getchar();
while(r<'0'||r>'9')r=getchar();
while(r>='0'&&r<='9'){
ans=ans*10+r-'0';r=getchar();}
return ans;
}
inline void addl(int u,int v,int w)
{
edge[cnt].e=v;
edge[cnt].v=w;
edge[cnt].nxt=head[u];
head[u]=cnt++;
}
void datasetting()
{
memset(head,-1,sizeof(head));
n=read();m=read();x=read();
int a,b,c;
for(int i=0;i<m;i++)
{
a=read();b=read();c=read();
addl(a,b,c);addl(b,a,0);//加边和反向边
}
}
bool bfs()//bfs找深度
{
memset(dis,-1,sizeof(dis));//注意!不要忘了这句
dis[1]=0;//起点深度为0,从源向汇bfs
queue<int>q;
q.push(1);
while(!q.empty())
{
int r=q.front();q.pop();
for(int i=head[r];i!=-1;i=edge[i].nxt)
{
int j=edge[i].e;
if(dis[j]==-1&&edge[i].v)//如果这个点还没有被bfs且这条边的流量不为0
{
dis[j]=dis[r]+1;
q.push(j);
}
}
}
return dis[n]!=-1;//若不可以到终点(起点)就返回false
}
int dfs(int u,int flo)//dfs就是求节点u及其子树在残量为flo时的最大增量
{
if(u==n)return flo;//如果是汇,直接返回flo
int detla=flo;//用一个变量来保存flo,以方便更新其剩余残量
for(int i=head[u];i!=-1;i=edge[i].nxt)
{
int v=edge[i].e;
if(dis[v]==(dis[u]+1)&&(edge[i].v)>0)//如果满足深度条件且边可以走
{
int d=dfs(v,min(detla,edge[i].v));//向下递归
//求v及其后续节点在残量为min(detla,edge[i].v)时的最大流量
edge[i].v-=d;edge[i ^ 1].v+=d;//边的处理
//注意,编号为i的边的反向边的编号为i^1,这是根据存边时的cnt决定的
detla-=d;//将本节点的剩余残量值更新
if(detla==0)break;//如果本节点已经没有残量可消耗了,就返回
}
}
return flo-detla;//返回这个点已经被允许流过的流量
}
int dini()//求最大流量
{
int ans=0;
while(bfs())
{
ans+=dfs(1,INF);//用INF是因为我们不知道此时的残量到底是多少(其实这个问题还是值得想一下)
}
return ans;
}
//**********************************main
int main()
{
freopen("datain.txt","r",stdin);
datasetting();
int a=dini();
if(a!=0)
if(x%a)printf("%d %d",a,(x-(x%a))/a+1);
else printf("%d %d",a,x/a);
else printf("Orz Ni Jinan Saint Cow!");
return 0;
}
/********************************************************************
ID:Andrew_82
LANG:C++
PROG:network-flows
********************************************************************/优化
当然,为了提高效率,我们可以引入一个叫做cur数组的东西
不知道是哪个家伙想出来的奇技淫巧
原理是什么呢?其实就是当我们在对一个节点u(假设有6儿子)进行增广时,把他的儿子1,2,3,4的可用流量都用完了,那么在下一次dfs模块走到u时,我们如果可以直接从儿子5开始进行增广就可以大大减少额外的时间开销
具体怎么实现?
我们可以在dfs里面做一点改动,即先定义一个cur数组,在dfs之前把邻接表的head数组拷贝到cur里面,然后在遍历u的时候同时把cur里面的边的下标后移,以达到将用完的边略去的目的
代码(加cur优化)
//P1343
#include<bits/stdc++.h>
using namespace std;
#define INF INT_MAX
const int maxn=200+5;
const int maxm=2000+5;
int n,m,x,cnt=0;
int head[maxn];
int dis[maxn];
struct node
{
int e;
int v;
int nxt;
}edge[maxm<<1];
int cur[maxn];
//**********************************function
inline int read(){
int ans=0;char r=getchar();
while(r<'0'||r>'9')r=getchar();
while(r>='0'&&r<='9'){
ans=ans*10+r-'0';r=getchar();}
return ans;
}
inline void addl(int u,int v,int w)
{
edge[cnt].e=v;
edge[cnt].v=w;
edge[cnt].nxt=head[u];
head[u]=cnt++;
}
void datasetting()
{
memset(head,-1,sizeof(head));
n=read();m=read();x=read();
int a,b,c;
for(int i=0;i<m;i++)
{
a=read();b=read();c=read();
addl(a,b,c);addl(b,a,0);
}
}
bool bfs()
{
memset(dis,-1,sizeof(dis));
dis[1]=0;
queue<int>q;
q.push(1);
while(!q.empty())
{
int r=q.front();q.pop();
for(int i=head[r];i!=-1;i=edge[i].nxt)
{
int j=edge[i].e;
if(dis[j]==-1&&edge[i].v)
{
dis[j]=dis[r]+1;
q.push(j);
}
}
}
return dis[n]!=-1;//若不可以到终点(起点)就返回false
}
int dfs(int u,int flo)//dfs就是求节点u在残量为flo时的最大增量
{
if(u==n)return flo;
int detla=flo;
for(int i=cur[u];i!=-1;i=edge[i].nxt)
{
cur[u]=edge[i].nxt;
int v=edge[i].e;
if(dis[v]==(dis[u]+1)&&(edge[i].v)>0)
{
int d=dfs(v,min(detla,edge[i].v));
edge[i].v-=d;edge[i ^ 1].v+=d;
detla-=d;
if(detla==0)break;
}
}
return flo-detla;//返回这个点已经被允许流过的流量
}
int dini()
{
int ans=0;
while(bfs())
{
for(int i=1;i<=n;i++)cur[i]=head[i];
ans+=dfs(1,INF);
}
return ans;
}
//**********************************main
int main()
{
datasetting();
int a=dini();
if(a!=0)
if(x%a)printf("%d %d",a,(x-(x%a))/a+1);
else printf("%d %d",a,x/a);
else printf("Orz Ni Jinan Saint Cow!");
return 0;
}
/********************************************************************
ID:Andrew_82
LANG:C++
PROG:network-flows
********************************************************************/衍生问题
鲁迅说:网络流的代码只有普及组难度,建模才是最重要的
最小费用最大流问题
问题
给出一个网络图,以及其源点和汇点,每条边已知其最大流量和单位流量费用,求出其网络最大流和在最大流情况下的最小费用。
实现
由于是要求在最大流的情况下来找最小花费,容易想到的一个方法就是先求出最大流,然后用一个深搜来找到最小值
好像是可以的,但是作为一个又懒又笨的蒟蒻,我没有去试过这种方法,而且估计裸的dfs会有很大的爆栈的可能性
那么他既然要求最小花费,我们不妨把这个最小花费看成边的权值,构建一个图用最短路算法来找到源点到各个点的最短距离
找到这个数据之后,我们就可以沿着最短路来进行增广,即在最短路中求到一条可行路然后修改其残量,我们可以保证其为最大流中的一部分的最小花费
不断的进行增广直到我们找到了全部值,然后得解,这就是将dinic和spfa结合起来的求解最小费用最大流问题的方法
具体代码如下 (luoguP3381)
#include<bits/stdc++.h>
using namespace std;
const int INF=INT_MAX;
const int maxn=5000+5,maxm=50000+5;
int n,m,s,t,cnt=0;
int head[maxn];
int dis[maxn];
int result=0;
int minfee=0;
bool vis[maxn];
struct node
{
int e;
int nxt;
int w;//指权值
int f;//指流量
}edge[maxm<<1];
//**********************************function
inline void addl(int u,int v,int flow,int cost)
{
edge[cnt].e=v;
edge[cnt].w=cost;
edge[cnt].f=flow;
edge[cnt].nxt=head[u];
head[u]=cnt++;
}
inline int read()
{
int ans=0;
char r=getchar();
while(r<'0'||r>'9')r=getchar();
while(r>='0'&&r<='9')
{
ans=ans*10+r-'0';
r=getchar();
}
return ans;
}
void datasetting()
{
memset(head,-1,sizeof(head));
n=read();m=read();s=read();t=read();
int ui,vi,wi,fi;
for(int i=0;i<m;i++)
{
ui=read();vi=read();wi=read();fi=read();//fi是单位流量费用,wi是最大流量
addl(ui,vi,wi,fi);//正向边的权值为fi,流量为wi
addl(vi,ui,0,-fi);//反向边的权值为-fi,流量为0
}
}
bool spfa(int u,int v)
{
for(int i=0;i<maxn;i++)dis[i]=INF;//spfa基本操作
memset(vis,false,sizeof(vis));//spfa的队列排重优化
dis[u]=0;
deque<int>d;//spfa的slf优化
d.push_back(u);
vis[u]=true;
while(!d.empty())
{
int ui=d.front();d.pop_front();vis[ui]=false;//ui是当前松弛的边的起点
for(int i=head[ui];i!=-1;i=edge[i].nxt)
{
int vi=edge[i].e;int w=edge[i].w;int f=edge[i].f;//vi是当前松弛的边的终点
if(f&&dis[vi]>dis[ui]+w)//如果当前边有残量且是最短路上的边就对其进行松弛
{
dis[vi]=dis[ui]+w;
if(!vis[vi])
{
if(!d.empty()&&dis[vi]<dis[d.front()])d.push_front(vi);
else d.push_back(vi);
}
}
}
}
return dis[t]!=INF;
}
int dfs(int u,int flow)
{
if(u==t)return flow;
int detla=flow;
vis[u]=true;
for(int i=head[u];i!=-1;i=edge[i].nxt)
{
int v=edge[i].e;int w=edge[i].w;int f=edge[i].f;
if(f&&!vis[v]&&dis[v]==dis[u]+w)//注意,一个点只能访问一次,这个可以用vis来维护(vis在spfa模块和dfs模块中都被用到,注意初始化)
{
int d=dfs(v,min(f,detla));
detla-=d;
edge[i].f-=d;edge[i^1].f+=d;
minfee+=d*w;//更新费用(单价x流量)
if(detla==0)break;
}
}
vis[u]=false;
return flow-detla;
}
void dinic()
{
result=0;
while(spfa(s,t))
{
memset(vis,false,sizeof(vis));
result+=dfs(s,INF);
}
printf("%d %d",result,minfee);
}
//**********************************main
int main()
{
freopen("datain.txt","r",stdin);
datasetting();
dinic();
return 0;
}
/********************************************************************
ID:Andrew_82
LANG:C++
PROG:network flow
********************************************************************/attention:
1.fi是单价,而非边权,实际的边权=流量 × \times ×单价
2.对于每一条可改进路,其流量都是一样的,因此在更新费用的时候就可以直接用 fi × \times ×流量 了
更高级的建模参考luogu-网络流24题
发布者:全栈程序员栈长,转载请注明出处:https://javaforall.cn/125494.html原文链接:https://javaforall.cn
边栏推荐
- Pod Scheduling Strategy: Affinity, Stain and Stain Tolerance
- np.nan, np.isnan, None, pd.isnull, pd.isna 整理与小结
- FreeRTOS创建任务--动态创建、静态创建
- MD5 detailed explanation (check file integrity)
- 1.3 Rapid Spanning Tree Protocol RSTP
- svg气球升起爆炸js特效
- 力扣151-颠倒字符串中的单词
- Do you really understand the business process service BPass?
- The 7 most commonly used data analysis thinking, solve 95% of the analysis problems
- 手撸架构,MongDB 面试50问
猜你喜欢
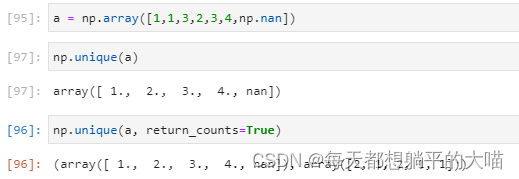
unique in numpy & pandas
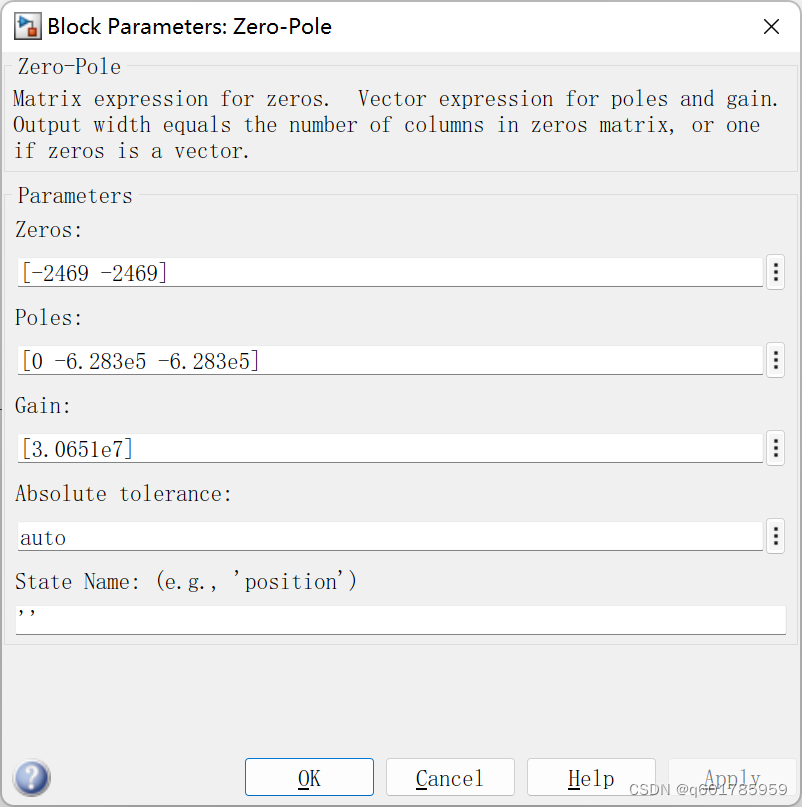
An example of type3 voltage loop compensator taking Boost as an example

Technology sharing | Description of the electronic fence function in the integrated dispatching system
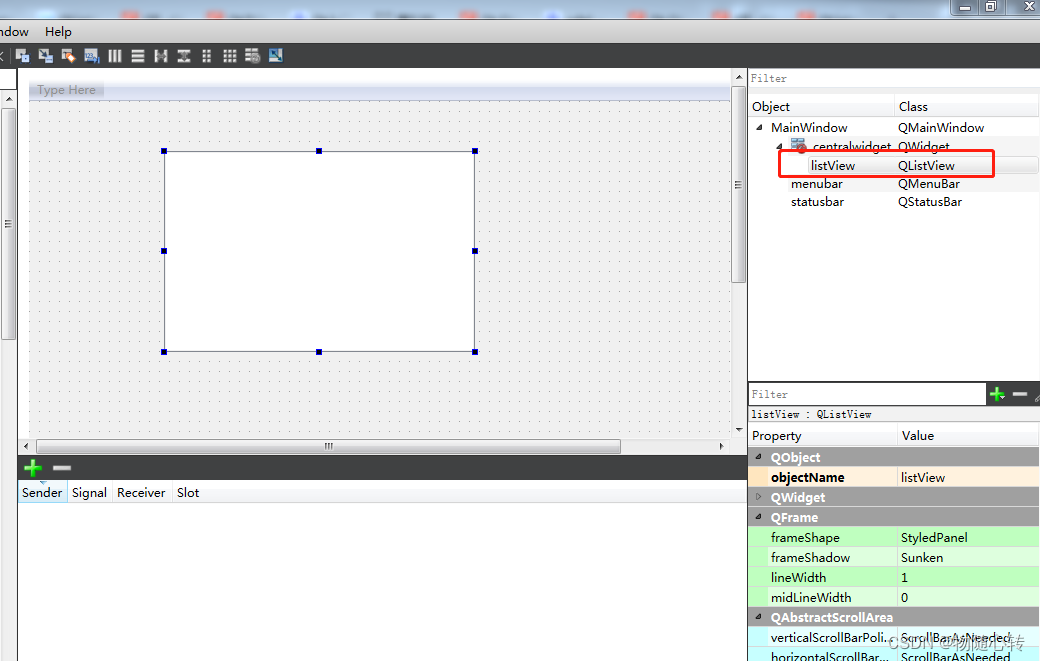
The use of QListView
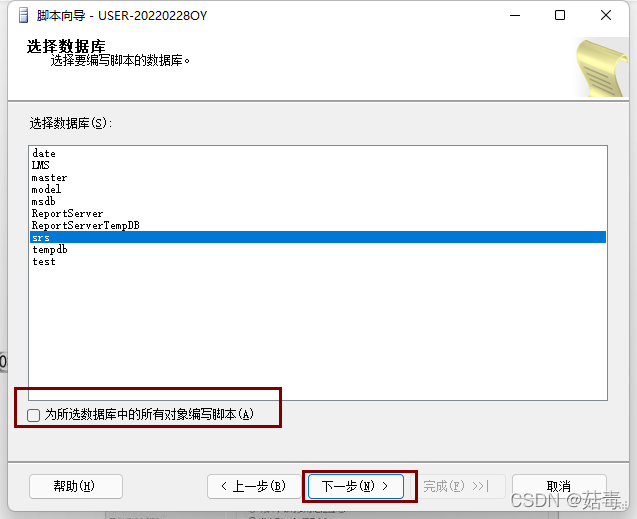
SQL Server 数据库之生成与执行 SQL 脚本

Thymeleaf
测试开发之路,我在大厂做测试这四年的感悟
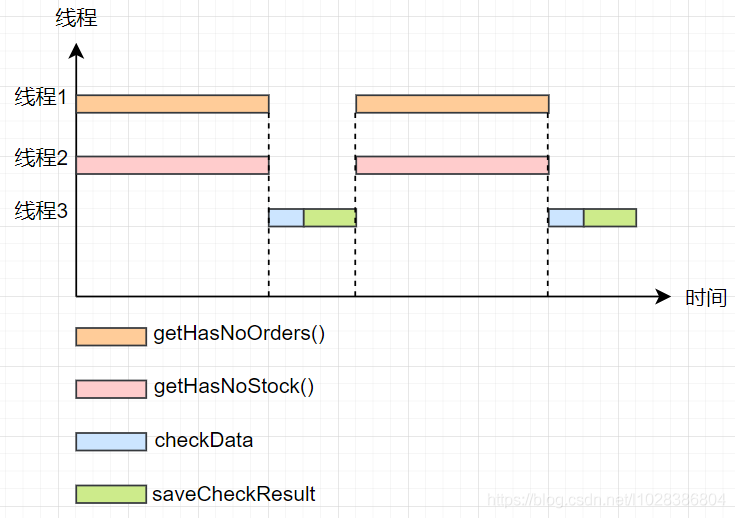
看我如何用多线程,帮助运营小姐姐解决数据校对系统变慢!
【The 6th Strong Net Cup CTF-Wp】
1.3快速生成树协议RSTP
随机推荐
SQL Server2019安装步骤及脱机安装Microsoft机器学习组件下一步不能继续的问题
智能图像分析-智能家用电器图像目标检测统计计数检测与识别-艾科瑞特科技(iCREDIT)
DTG-SSOD:最新半监督检测框架,Dense Teacher(附论文下载)
np.nan, np.isnan, None, pd.isnull, pd.isna 整理与小结
pgsql数据库实现导入导出
前男友买辣椒水威胁要抢女儿,女方能否申请人身安全保护令?
Import and export data of SQL Server database
Hand rolled architecture, 41 Redis interview asked
图神经网络(GNN)的简介「建议收藏」
Transfer files between servers
Solve the problem of Chinese garbled characters in exporting excel file names
After Effects 教程,如何在 After Effects 中对蒙版进行动画绘制?
sql concat()函数
30 lines of code to realize serverless real-time health code recognition -- operation manual
Golang map数组按字段分类
1.3快速生成树协议RSTP
Do you really understand the business process service BPass?
SQL Server修改数据
如何关闭开启硬件加速[通俗易懂]
手撸架构,Mysql 面试126问