当前位置：网站首页>【GCN-RS】UltraGCN: Ultra Simplification of Graph Convolutional Networks for Recommendation (CIKM‘21)

【GCN-RS】UltraGCN: Ultra Simplification of Graph Convolutional Networks for Recommendation (CIKM‘21)

2022-06-22 06:54:00 【chad_ lee】

UltraGCN: Ultra Simplification of Graph Convolutional Networks for Recommendation (CIKM’21 Huawei Noah Ark )

（ I forgot to send the article in the draft box , For more than two months ）

The article analyzes LightGCN Three shortcomings of , And a kind of Extremely simplified GCN Recommended model , Almost degree weighted MF, No, message passing、aggregation, With two auxiliary loss Introduce graph structure information into MF, To put Amazon-Book The data set exploded , The velocity is LightGCN Of 15 times , The effect is improved 60%, It can be said that the road is simple , Recover one's original simplicity , The feeling is MF+ItemCF Model fusion . At the same time, there is also the idea of false labels in it .

LightGCN Three major shortcomings

One disadvantage ： The edge weight of message aggregation is counterintuitive

LightGCN Message aggregation for ：
$\begin{aligned} &e_{u}^{(l+1)}=\frac{1}{d_{u}+1} e_{u}^{(l)}+\sum_{k \in \mathcal{N}(u)} \frac{1}{\sqrt{d_{u}+1} \sqrt{d_{k}+1}} e_{k}^{(l)} \\ &e_{i}^{(l+1)}=\frac{1}{d_{i}+1} e_{i}^{(l)}+\sum_{v \in \mathcal{N}(i)} \frac{1}{\sqrt{d_{v}+1} \sqrt{d_{i}+1}} e_{v}^{(l)} \end{aligned}$
Dot product ：
$\begin{gathered} e_{u}^{(l+1)} \cdot e_{i}^{(l+1)}=\alpha_{u i}\left(e_{u}^{(l)} \cdot e_{i}^{(l)}\right)+\sum_{k \in \mathcal{N}(u)} \alpha_{i k}\left(e_{i}^{(l)} \cdot e_{k}^{(l)}\right)+ \\ \sum_{v \in \mathcal{N}(i)} \alpha_{u v}\left(e_{u}^{(l)} \cdot e_{v}^{(l)}\right)+\sum_{k \in \mathcal{N}(u)} \sum_{v \in \mathcal{N}(i)} \alpha_{k v}\left(e_{k}^{(l)} \cdot e_{v}^{(l)}\right) \end{gathered}$
And the weight $\alpha$ ：
$\begin{aligned} \alpha_{u i} &=\frac{1}{\left(d_{u}+1\right)\left(d_{i}+1\right)} \\ \alpha_{i k} &=\frac{1}{\sqrt{d_{u}+1} \sqrt{d_{k}+1}\left(d_{i}+1\right)} \\ \alpha_{u v} &=\frac{1}{\sqrt{d_{v}+1} \sqrt{d_{i}+1}\left(d_{u}+1\right)} \\ \alpha_{k v} &=\frac{1}{\sqrt{d_{u}+1} \sqrt{d_{k}+1} \sqrt{d_{v}+1} \sqrt{d_{i}+1}} \end{aligned}$
therefore $\alpha_{ik}$ Is used to model item-item Of the relationship , But for a user, goods $i$ And objects $k$ The weight of is asymmetric ( $\frac{1}{\sqrt{d_{k}+1}}$ for $k$ , $\frac{1}{d_{i}+1}$ for $i$ ). Accordingly, for modeling user-user Relationship , There are also unequal weights .

Such unreasonable weight assignments may mislead the model training and finally result in sub-optimal performance.

But I don't think this is the key issue , For data $e_u*e_i$ unequal , For data $e_u*e_k$ And inequality , But the two train together , Isn't it equal ？

Disadvantages two ： Message aggregation has a small amount of information

All types of messages are aggregated , It does not distinguish between message types , No distinction is made between importance , There may also be noise , It should be different relationships Give different importance .

But I don't think this is the key issue , There are not already in the message transmission $\frac{1}{\sqrt{d_{u}+1} \sqrt{d_{k}+1}}$ As a weight of importance ？ The author's later weight of importance is essentially the same as this . The corresponding solution to this problem should be attentive The aggregation of .

Disadvantages three ：Over-smoothing

That's the point .

UltraGCN Study User-Item Graph

When GCN After infinite layers of messaging , The characterization of the last two layers should be the same ：
$e_{u}=\lim _{l \rightarrow \infty} e_{u}^{(l+1)}=\lim _{l \rightarrow \infty} e_{u}^{(l)}$
So message aggregators can write ：
$e_{u}=\frac{1}{d_{u}+1} e_{u}+\sum_{i \in \mathcal{N}(u)} \frac{1}{\sqrt{d_{u}+1} \sqrt{d_{i}+1}} e_{i}$
Simplify ：
$e_{u}=\sum_{i \in \mathcal{N}(u)} \beta_{u, i} e_{i}, \quad \beta_{u, i}=\frac{1}{d_{u}} \sqrt{\frac{d_{u}+1}{d_{i}+1}}$
So the above formula is the representation when all nodes converge . The author wants to communicate without displaying messages , Optimize directly to this state ：

So the goal of optimization is to minimize the gap between the two sides of the equation , In other words, maximize the inner product of both sides ：
$\max \sum_{i \in \mathcal{N}(u)} \beta_{u, i} e_{u}^{\top} e_{i}, \quad \forall u \in U$
This is equivalent to maximizing $e_u$ and $e_i$ Cosine similarity of . For the sake of optimization , Also join sigmoid and negative log likelihood, therefore loss：
$\mathcal{L}_{C}=-\sum_{u \in U} \sum_{i \in \mathcal{N}(u)} \beta_{u, i} \log \left(\sigma\left(e_{u}^{\top} e_{i}\right)\right)$
But there are also over- smoothing The problem of , Would it be good if all the connected points were the same length ？ So negative sampling can solve over- smoothing：
$\mathcal{L}_{C}=-\sum_{(u, i) \in N^{+}} \beta_{u, i} \log \left(\sigma\left(e_{u}^{\top} e_{i}\right)\right)-\sum_{(u, j) \in N^{-}} \beta_{u, j} \log \left(\sigma\left(-e_{u}^{\top} e_{j}\right)\right)$
here $\beta_{u,i}$ The function is to control degree A little bit smaller , The impact will be greater ,degree The bigger the point, the smaller the impact .（ This discord LightGCN The edge weight of ？）

hold RS Task as link prediction Mission , The main part of the model loss Also need not BPR loss, use BCE Loss：
$\mathcal{L}_{O}=-\sum_{(u, i) \in N^{+}} \log \left(\sigma\left(e_{u}^{\top} e_{i}\right)\right)-\sum_{(u, j) \in N^{-}} \log \left(\sigma\left(-e_{u}^{\top} e_{j}\right)\right)$

$\mathcal{L}=\mathcal{L}_{O}+\lambda \mathcal{L}_{C}$

The model here is recorded as $UltraGCN_{Base}$ , Intuitively understanding is in MF Based on the model , Let model reinforcement remember connected edges .

UltraGCN Study Item-Item Graph

GCN The model passes messages , Also learned implicitly item-item、user-user The relationship between , Here is how to learn item-item Relationship .

Construct a item-item Co-occurrence matrix $\in \mathcal{R}^{|I| \times|I|}$ ：
$\begin{aligned} &G=A^{\top} A \end{aligned}$
$G_{i,j}$ Representative items i And objects j The co-occurrence times of . Define an item i and j The coefficient of $\omega_{i, j}$ ：
$\omega_{i, j}=\frac{G_{i, j}}{g_{i}-G_{i, i}} \sqrt{\frac{g_{i}}{g_{j}}}, \quad g_{i}=\sum_{k} G_{i, k}$
But compared with adjacency graph $A$ , chart $G$ very dense, You can't learn everything , The noise will be greater than the information .

Since the picture is too dense, Then make it sparse： according to $\omega_{i, j}$ , Only the most similar K A neighbor item $S (i)$ .

Compared with direct learning item-item Relationship , The article is ingenious augment positive user-item pairs to capture item-item relationships：
$\mathcal{L}_{I}=-\sum_{(u, i) \in N^{+}} \sum_{j \in S(i)} \omega_{i, j} \log \left(\sigma\left(e_{u}^{\top} e_{j}\right)\right)$
This is not to take ItemCF As a fake tag ！

therefore UltraGCN Of loss Namely ：
$\mathcal{L}=\mathcal{L}_{O}+\lambda \mathcal{L}_{C}+\gamma \mathcal{L}_{I}$
Here the model is very flexible , Any relationship can be learned ：user-item, item-item, user-user, Knowledge map, etc . But here user-user The graph structure has no obvious improvement , because users’ interests are much broader than items’ attributes. Why does this go south 《Multi-behavior Recommendation with Graph Convolutional Networks》 Also used and explained .

UltraGCN Separate the relationships , Study alone , The effect must be better than GCN-based CF Mixed in with message passing The effect is good .

therefore UltraGCN and WRMF It's like , If at first WRMF We can use graph structure to give weight , There is no present GCN What happened to the model .

experimental result

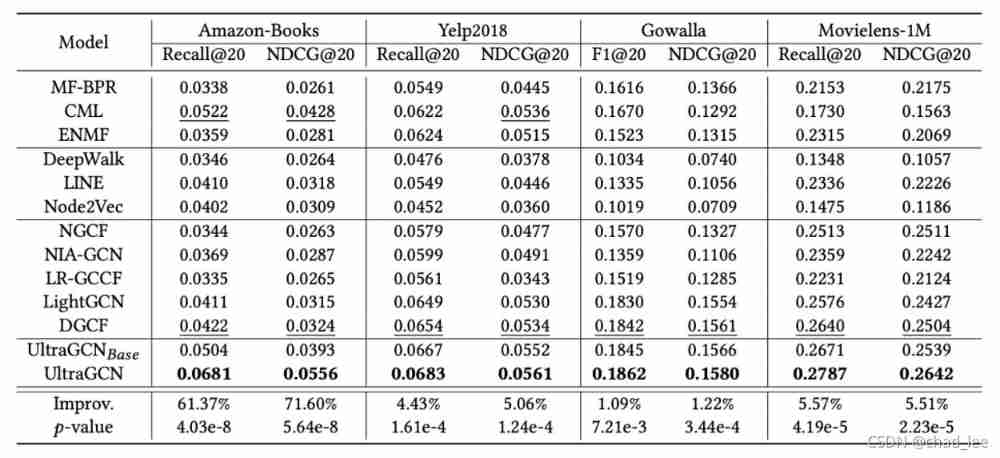
Insert picture description here

In addition, it also compares SCF, LCFN, NBPO, BGCF, and SGL-ED.
Insert picture description here

原网站

版权声明
本文为[chad_ lee]所创，转载请带上原文链接，感谢
https://yzsam.com/2022/02/202202220543470571.html