Travel (split points and layers)

https://ac.nowcoder.com/acm/contest/37782/I

The question
Given n A little bit m An undirected graph of edges , Each side has a cost $w_i$.
Starting from 1, The finish for n.
For a path from the beginning to the end , It takes you $x$.
ask , What is the minimum cost from the beginning to the end ？
$(1\le n,x\le 10^5,n-1\le m\le 2\times 10^5)$

Ideas
Analyze the topic and know , For a path , Its cost depends not only on the sum of edge weights , It also depends on the path length . The longer the path , More even points , It's going to cost a lot x. So you can't simply run the shortest way .

The cost from one point to the next is different , In addition to the edge right , Also consider whether the current point is odd or even . Odd and even points are connected .

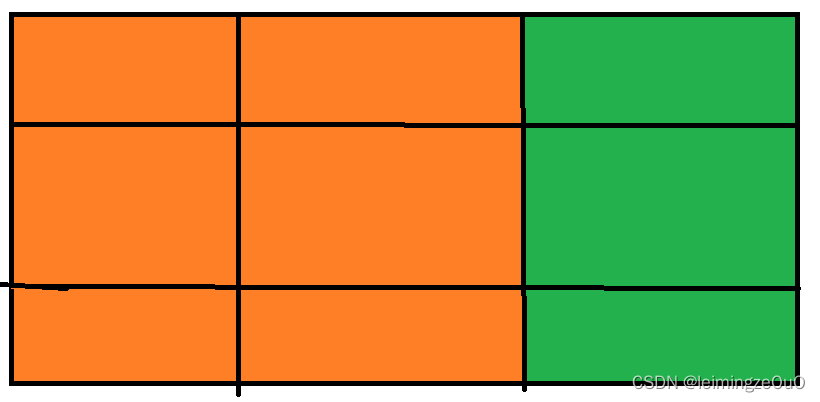
You can split each point into two points , They are odd points and even points .
Put all the odd points on the first layer , All even points are placed on the second floor . Connect the edges from the first floor to the second floor every time , From the second floor to the first floor , In this way, odd points and even points are connected .
Because it costs to reach even points x, This cost can be added to the edge right , When connecting the edge from the first floor to the second floor , Edge weight plus x.

Then from the first floor 1 Start running at No , Take it to the first floor n Point number and the second floor n The minimum value of the shortest distance of point is the minimum cost .

Code

#include<bits/stdc++.h>
using namespace std;

#define Ios ios::sync_with_stdio(false),cin.tie(0)
#define int long long

const int N = 200010, mod = 1e9+7;
int T, n, m;
int a[N];
int k;
int dist[N], f[N];
vector<PII> e[N];
int ans;

void dij()
{
    
	priority_queue<PII, vector<PII>, greater<PII> > que;
	que.push({
    0, 1});
	
	for(int i=1;i<=2*n;i++) dist[i] = 1e18;
	dist[1] = 0;
	
	while(que.size())
	{
    
		int x = que.top().se; que.pop();
		if(f[x]) continue;
		f[x] = 1;
		
		if(x == n || x == n + n){
    
			ans = dist[x];
			return;
		}
		
		for(auto it : e[x])
		{
    
			int tx = it.fi, dis = it.se;
			if(dist[tx] > dist[x] + dis){
    
				dist[tx] = dist[x] + dis;
				que.push({
    dist[tx], tx});
			}
		}
	}
}

signed main(){
    
	Ios;
	cin >> n >> m >> k;
	while(m--)
	{
    
		int x, y, z; cin >> x >> y >> z;
		int nex = n + x, ney = n + y;
		e[x].push_back({
    ney, z + k});
		e[ney].push_back({
    x, z});
		e[nex].push_back({
    y, z});
		e[y].push_back({
    nex, z + k});
	}
	
	dij();
	
	cout << ans;
	
	return 0;
}

Experience
The idea of dismantling points should be mastered .

---

seek 1-n All prime factors of each number in

The complexity of directly decomposing prime factors for each number is $O(n\sqrt{n})$,1e6 You can't run .

Think the other way around , Consider which numbers each prime factor is in .
For each prime factor , It must be the prime factor of all its multiples .
Then it can be in the sieve , Traverse all its multiples , Put the current prime factor into the multiple vector in , At the same time, mark the number as a non prime number , Will not traverse its multiples .
such , The Egyptian sieve ensures that the traversal is prime , Traversing all multiples ensures that it is a factor , stay $O(nlogn)$ Within the complexity of 1-n this n All prime factors of numbers .

#include<bits/stdc++.h>
using namespace std;

const int N = 2000010, mod = 1e9+7;
int T, n, m;
vector<int> v[N];
int f[N];

void Prim()
{
    
	for(int i=2;i<=n;i++)
	{
    
		if(f[i]) continue;
		v[i].push_back(i);
		
		for(int j=i+i;j<=n;j+=i){
    
			v[j].push_back(i);
			f[j] = 1;
		}
	}
}

signed main(){
    
	cin >> n;
	Prim();
	
	for(int i=1;i<=n;i++)
	{
    
		cout << i << " : ";
		for(int x : v[i]) cout << x << " ";
		cout << endl;
	}
	return 0;
}

---

Magic number

The question
Find all positive integers x , bring $a\equiv b\equiv c(\mathrm{mod}x)$ .
Please output all... From small to large x Possible values , If there are infinite possibilities x, The output -1 .

Ideas
Find the two numbers first x, Then judge that another number symbol does not match .
$a\equiv b(\mathrm{mod}x)$ Turn into $(a-b)\mathrm{mod}x=0$.
that x yes $|a-b|$ The divisor of .
Traverse all its divisors to see c Whether it conforms to .

When a=b=c when ,x Take any value .
otherwise Take two different numbers Subtract for divisor .

Code

#include<bits/stdc++.h>
using namespace std;

const int N = 200010, mod = 1e9+7;
int T, n, m;
int a[N];

signed main(){
    
	cin >> T;
	while(T--)
	{
    
		int x, y, z;
		cin >> x >> y >> z;
		if(x == y && y == z){
    
			cout << -1 << endl;
			continue;
		}
		
		set<int> st;
		
		int n;
		if(x != y) n = abs(x - y);
		else n = abs(x - z);
		
		for(int i=1;i<=n/i;i++)
		{
    
			if(n % i == 0)
			{
    
				if(x % i == y % i && x % i == z % i){
    
					st.insert(i);
				}
				int tt = n/i;
				if(tt == i) continue;
				if(x % tt == y % tt && x % tt == z % tt){
    
					st.insert(tt);
				}
			}
		}
		for(int x : st) cout << x << " ";
		cout << endl;
	}
	
	return 0;
}

x mod y = 0, y It must be x The divisor of .