当前位置:网站首页>Kalman滤波器--从高斯融合推导
Kalman滤波器--从高斯融合推导
2022-06-30 17:49:00 【古路】
Kalman滤波器--从高斯融合推导
0.引言
“如果古希腊人知道正态分布,想必奥林匹斯山的神殿里会多出一个正态女神,由她来掌管世间的混沌!”
1.贝叶斯法则
- 另一种推导方式,从误差角度的推导?参考之前的推导。之前的推导过于繁琐,感觉更多的是数学上的推导,从贝叶斯法则以及高斯融合的角度推导,则物理意义十分明确,更加的浅显易懂。
- 一句话总结就是贝叶斯法则+高斯融合:根据贝叶斯法则有,后验估计 ∝ \propto ∝ 似然 * 先验 ,参考链接;然后根据假设(误差服从高斯分布),通过高斯分布的性质,将 似然项高斯分布 和 先验项高斯分布 相乘就得到了后验估计的分布。
这篇文章看到这里就够了。
状态估计问题的求解思路:
假设系统 k k k 时刻的观测量为 z k z_k zk ,状态量为 x k x_k xk ,这两个变量是符合某种分布的随机变量,且它们不相互独立。我们希望求出:
P ( x k ∣ x 0 , z 1 : k ) P\left(\boldsymbol{x}_{k} \mid \boldsymbol{x}_{0}, \boldsymbol{z}_{1: k}\right) P(xk∣x0,z1:k)
根据贝叶斯法则,(估计中的概率公式参考)将系统状态的概率求解拆分如下:
P ( x k ∣ x 0 , z 1 : k ) ∝ P ( z k ∣ x k ) P ( x k ∣ x 0 , z 1 : k − 1 ) P\left(\boldsymbol{x}_{k} \mid \boldsymbol{x}_{0}, \boldsymbol{z}_{1: k}\right) \propto P\left(\mathbf{z}_{k} \mid \boldsymbol{x}_{k}\right) P\left(\boldsymbol{x}_{k} \mid \boldsymbol{x}_{0}, \boldsymbol{z}_{1: k-1}\right) P(xk∣x0,z1:k)∝P(zk∣xk)P(xk∣x0,z1:k−1)
假设系统 满足马尔可夫性质,即 x k x_k xk 仅与 x K − 1 x_{K-1} xK−1 相关,与更早的状态无关(如下图),可进一步简化为:

P ( x k ∣ x 0 , z 1 : k ) ∝ P ( z k ∣ x k ) P ( x k ∣ x k − 1 ) P\left(\boldsymbol{x}_{k} \mid \boldsymbol{x}_{0}, \boldsymbol{z}_{1: k}\right) \propto P\left(\mathbf{z}_{k} \mid \boldsymbol{x}_{k}\right) P\left(\boldsymbol{x}_{k} \mid \boldsymbol{x}_{k-1}\right) P(xk∣x0,z1:k)∝P(zk∣xk)P(xk∣xk−1)
其中:
- P ( z k ∣ x k ) P\left(\mathbf{z}_{k} \mid \boldsymbol{x}_{k}\right) P(zk∣xk) 为似然项,可由观测方程给出
- P ( x k ∣ x k − 1 ) P\left(\boldsymbol{x}_{k} \mid \boldsymbol{x}_{k-1}\right) P(xk∣xk−1) 为先验项,可通过状态转移方程推导得到
该问题可用滤波器相关算法解决,如Kalman Filter或Extented Kalman Filter。
在状态估计时:
p ( x ∣ y ) = p ( y ∣ x ) p ( x ) p ( y ) p(\boldsymbol{x} \mid \boldsymbol{y})=\frac{p(\boldsymbol{y} \mid \boldsymbol{x}) p(\boldsymbol{x})}{p(\boldsymbol{y})} p(x∣y)=p(y)p(y∣x)p(x)
赋予该式物理意义:
- x x x : 状态,可由状态转移方程推出,也称为先验
- y y y :传感器读数
- p ( y ∣ x ) p(y|x) p(y∣x) : 传感器模型,可由观测方程给出,也称为似然
- p ( x ∣ y ) p(x|y) p(x∣y) : 状态估计, 也称后验
因此贝叶斯估计: 后验估计 ∝ \propto ∝ 似然 * 先验 。参考链接。
2.kalman推导
从一个例子开始,定义 k k k 时刻的系统的状态为 x k x_k xk ,假设包含位置和速度两部分:
x k = [ p k v k ] x_{k}=\left[\begin{array}{l} p_{k} \\ v_{k} \end{array}\right] xk=[pkvk]
为进一步表示 x k x_k xk 各成员的不确定性和各维度之间的相互关系,引入协方差矩阵:
P k = [ Σ p p Σ p v Σ v p Σ v v ] \boldsymbol{P}_{k}=\left[\begin{array}{cc} \Sigma_{p p} & \Sigma_{p v} \\ \Sigma_{v p} & \Sigma_{v v} \end{array}\right] Pk=[ΣppΣvpΣpvΣvv]
其中:
- Σ p p \Sigma_{p p} Σpp 和 Σ v v \Sigma_{v v} Σvv 为状态分量的方差
- Σ v p \Sigma_{v p} Σvp 和 Σ p v \Sigma_{p v} Σpv 描述 p p p 和 v v v 之间协方差

如上图(左),速度和位置关系是独立的,因为其方差互相不受影响;而图(右)则相反。
进一步,已知 k − 1 k − 1 k−1 时刻的状态 x k − 1 x_{k-1} xk−1 ,我们首先可以通过运动关系预测其 k k k 时刻的状态 x k x_k xk 。
情况1:假设短时间内满足匀速运动的条件:
x ‾ k = [ 1 Δ t 0 1 ] x ^ k − 1 = F k x ^ k − 1 \overline{\boldsymbol{x}}_{k}=\left[\begin{array}{cc} 1 & \Delta t \\ 0 & 1 \end{array}\right] \widehat{\boldsymbol{x}}_{k-1}=\boldsymbol{F}_{k} \widehat{\boldsymbol{x}}_{k-1} xk=[10Δt1]xk−1=Fkxk−1
其中:
- x ‾ k \overline{\boldsymbol{x}}_{k} xk 为 k k k 时刻的先验分布
- x ^ k − 1 \widehat{\boldsymbol{x}}_{k-1} xk−1 为 k − 1 k − 1 k−1 时刻的后验分布
- F k \boldsymbol{F}_{k} Fk 为状态转移矩阵

情况2:以上状态转移的过程,是系统没有任何外部干预的情况下匀速运动,但试想如果在运动过程中有外界影响会怎么样呢? 比如,人为地推了一下。
x ‾ k = F k x ^ k − 1 + B k u k \overline{\boldsymbol{x}}_{k}=\boldsymbol{F}_{k} \widehat{\boldsymbol{x}}_{k-1}+\boldsymbol{B}_{k} \boldsymbol{u}_{k} xk=Fkxk−1+Bkuk
其中:
- u k \boldsymbol{u}_{k} uk 表示外部输入
- B k \boldsymbol{B}_{k} Bk 表示外部输入与系统状态变化的转换关系矩阵
情况3:在上述的系统状态建模中,均是理想化的模型,没有考虑系统噪声。为更好地建模系统状态转换关系,我们引入高斯噪声项来模拟系统噪声。考虑噪声后的 x ‾ k \overline{\boldsymbol{x}}_{k} xk 如下:
x ‾ k = F k x ^ k − 1 + B k u k + w k (1) \textcolor{blue}{\overline{\boldsymbol{x}}_{k}=\boldsymbol{F}_{k} \widehat{\boldsymbol{x}}_{k-1}+\boldsymbol{B}_{k} \boldsymbol{u}_{k}+\boldsymbol{w}_{k}}\tag{1} xk=Fkxk−1+Bkuk+wk(1)
其中:
- w k ∼ N ( 0 , Q k ) \boldsymbol{w}_{k} \sim N\left(0, \boldsymbol{Q}_{k}\right) wk∼N(0,Qk) 为高斯噪声
C o v ( x ) = Σ Cov(x) = \boldsymbol{Σ} Cov(x)=Σ ,根据协方差矩阵的性质:
Cov ( A x ) = A Σ A T \operatorname{Cov}(\boldsymbol{A} \boldsymbol{x})=\boldsymbol{A} \boldsymbol{\Sigma} \boldsymbol{A}^{T} Cov(Ax)=AΣAT贝叶斯法则以及高斯融合
对于预测而来的状态,可以描述为:
Cov ( x ^ k − 1 ) = P ^ k − 1 x ‾ k = F k x ^ k − 1 } ⇒ Cov ( x ‾ k ) = Cov ( F k x ^ k − 1 ) = F k P ^ k − 1 F k T \left.\begin{array}{c} \operatorname{Cov}\left(\widehat{\boldsymbol{x}}_{k-1}\right)=\widehat{\boldsymbol{P}}_{k-1} \\ \overline{\boldsymbol{x}}_{k}=\boldsymbol{F}_{k} \widehat{\boldsymbol{x}}_{k-1} \end{array}\right\} \Rightarrow \operatorname{Cov}\left(\overline{\boldsymbol{x}}_{k}\right)=\operatorname{Cov}\left(\boldsymbol{F}_{k} \widehat{\boldsymbol{x}}_{k-1}\right)=\boldsymbol{F}_{k} \widehat{\boldsymbol{P}}_{k-1} \boldsymbol{F}_{k}^{T} Cov(xk−1)=Pk−1xk=Fkxk−1}⇒Cov(xk)=Cov(Fkxk−1)=FkPk−1FkT
即是:
P ‾ k = F k P ^ k − 1 F k T \overline{\boldsymbol{P}}_{k}=\boldsymbol{F}_{k} \widehat{\boldsymbol{P}}_{k-1} \boldsymbol{F}_{k}^{T} Pk=FkPk−1FkT
考虑噪声的 x ‾ k \overline{\boldsymbol{x}}_{k} xk, 其协方差可记为:
P ‾ k = F k P ^ k − 1 F k T + Q k (2) \textcolor{blue}{\overline{\boldsymbol{P}}_{k}=\boldsymbol{F}_{k} \widehat{\boldsymbol{P}}_{k-1} \boldsymbol{F}_{k}^{T}+\boldsymbol{Q}_{k}}\tag{2} Pk=FkPk−1FkT+Qk(2)
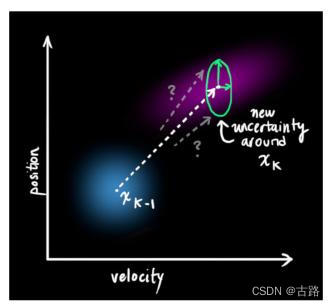
根据 k − 1 k − 1 k−1 时刻的后验状态 x ^ k − 1 \widehat{\boldsymbol{x}}_{k-1} xk−1,我们可以预测出 k k k 时刻的先验状态 x ‾ k \overline{\boldsymbol{x}}_{k} xk 以及其协方差矩阵 p ‾ k \overline{\boldsymbol{p}}_{k} pk :
x ‾ k = F k x ^ k − 1 + B k u k + w k (1) \overline{\boldsymbol{x}}_{k}=\boldsymbol{F}_{k} \widehat{\boldsymbol{x}}_{k-1}+\boldsymbol{B}_{k} \boldsymbol{u}_{k}+\boldsymbol{w}_{k}\tag{1} xk=Fkxk−1+Bkuk+wk(1)
x ‾ k \overline{\boldsymbol{x}}_{k} xk 满足如下分布:
N ( x ‾ k , P ‾ k ) = N ( F k x ^ k − 1 + B k u k , F k P ^ k − 1 F k T + Q k ) (2) \textcolor{blue}{N\left(\overline{\boldsymbol{x}}_{k}, \overline{\boldsymbol{P}}_{k}\right)=N\left(\boldsymbol{F}_{k} \widehat{\boldsymbol{x}}_{k-1}+\boldsymbol{B}_{k} \boldsymbol{u}_{k}, \boldsymbol{F}_{k} \widehat{\boldsymbol{P}}_{k-1} \boldsymbol{F}_{k}^{T}+\boldsymbol{Q}_{k}\right)}\tag{2} N(xk,Pk)=N(Fkxk−1+Bkuk,FkPk−1FkT+Qk)(2)
当获得 k k k 时刻的系统观测量 z k \boldsymbol{z}_k zk 时,可以尝试通过 z k \boldsymbol{z}_k zk 重新修正 k k k 时刻的后验状态 x ^ k \widehat{\boldsymbol{x}}_{k} xk 及其协方差矩阵 p ^ k \widehat{\boldsymbol{p}}_{k} pk.
假设通过一些传感器测量的 z k = ( p o s i t i o n , v e l o c i t y ) \boldsymbol{z}_k = (position, velocity) zk=(position,velocity) ,这样可以得到如下结果:
z k = x ‾ k \boldsymbol{z}_k = \overline{\boldsymbol{x}}_{k} zk=xk
为了进一步泛化观测量 z k \boldsymbol{z}_k zk 与状态量 x ‾ k \overline{\boldsymbol{x}}_{k} xk 之间的关系,定义观测矩阵 H k {\boldsymbol{H}}_{k} Hk:
z k = H k x ‾ k (3) \boldsymbol{z}_k = {\boldsymbol{H}}_{k}\overline{\boldsymbol{x}}_{k}\tag{3} zk=Hkxk(3)
根据协方差矩阵的性质,可推导出观测量的方差为:
Σ = H k P ‾ k H k T (4) \boldsymbol{\Sigma}=\boldsymbol{H}_{k} \overline{\boldsymbol{P}}_{k} \boldsymbol{H}_{k}^{T}\tag{4} Σ=HkPkHkT(4)
进一步,在考虑观测的高斯噪声的情况下 v k \boldsymbol{v}_k vk 满足 N ( 0 , R k ) N(0,\boldsymbol{R}_k) N(0,Rk)分布 ,可得出下式:
z k = H k x ‾ k + v k (5) \boldsymbol{z}_k={\boldsymbol{H}}_{k}\overline{\boldsymbol{x}}_{k} + \boldsymbol{v}_k \tag{5} zk=Hkxk+vk(5)
z k \boldsymbol{z}_k zk 满足如下分布:
N ( z k , Σ ) = N ( H k x ‾ k , H k P ‾ k H k T + R k ) (6) N\left(\boldsymbol{z}_{k}, \boldsymbol{\Sigma}\right)=N\left(\boldsymbol{H}_{k} \overline{\boldsymbol{x}}_{\boldsymbol{k}}, \boldsymbol{H}_{k} \overline{\boldsymbol{P}}_{k} \boldsymbol{H}_{k}^{T}+\boldsymbol{R}_{k}\right)\tag{6} N(zk,Σ)=N(Hkxk,HkPkHkT+Rk)(6)
其中,公式(2) 描述了 x ‾ k \overline{\boldsymbol{x}}_{k} xk 的分布,公式(6) 描述了 z k \boldsymbol{z}_k zk 的分布。
高斯分布知识回顾:

两个高斯分布的乘积依然是高斯分布,而且为了得到两个高斯分布的重叠部分的分布函数,我们通常将两个高斯分布相乘。
N ( x , μ ′ , σ ′ ) = N ( x , μ 0 , σ 0 ) ⋅ N ( x , μ 1 , σ 1 ) N\left(x, \mu^{\prime}, \sigma^{\prime}\right)=N\left(x, \mu_{0}, \sigma_{0}\right) \cdot N\left(x, \mu_{1}, \sigma_{1}\right) N(x,μ′,σ′)=N(x,μ0,σ0)⋅N(x,μ1,σ1)
由 N ( x , μ , σ ) = 1 σ 2 π e − ( x − μ ) 2 2 σ 2 N(x, \mu, \sigma)=\frac{1}{\sigma \sqrt{2 \pi}} e^{-\frac{(x-\mu)^{2}}{2 \sigma^{2}}} N(x,μ,σ)=σ2π1e−2σ2(x−μ)2推导可得:
μ ′ = μ 0 + σ 0 2 ( μ 1 − μ 0 ) σ 0 2 + σ 1 2 σ ′ 2 = σ 0 2 − σ 0 4 σ 0 2 + σ 1 2 \begin{aligned} &\mu^{\prime}=\mu_{0}+\frac{\sigma_{0}^{2}\left(\mu_{1}-\mu_{0}\right)}{\sigma_{0}^{2}+\sigma_{1}^{2}} \\ &\sigma^{\prime 2}=\sigma_{0}^{2}-\frac{\sigma_{0}^{4}}{\sigma_{0}^{2}+\sigma_{1}^{2}} \end{aligned} μ′=μ0+σ02+σ12σ02(μ1−μ0)σ′2=σ02−σ02+σ12σ04
假设 k = σ 0 2 σ 0 2 + σ 1 2 k = \frac{\sigma_{0}^{2}}{\sigma_{0}^{2}+\sigma_{1}^{2}} k=σ02+σ12σ02,上式可化简为:
μ ′ = μ 0 + K ( μ 1 − μ 0 ) σ ′ 2 = σ 0 2 − K σ 0 2 \begin{aligned} &\mu^{\prime}=\mu_{0}+K\left(\mu_{1}-\mu_{0}\right) \\ &\sigma^{\prime 2}=\sigma_{0}^{2}-K \sigma_{0}^{2} \end{aligned} μ′=μ0+K(μ1−μ0)σ′2=σ02−Kσ02
将上式扩展到多维空间:
K = Σ 0 ( Σ 0 + Σ 1 ) − 1 μ ′ = μ 0 + K ( μ 1 − μ 0 ) Σ ′ = Σ 0 + K Σ 0 \begin{gathered} \boldsymbol{K}=\boldsymbol{\Sigma}_{0}\left(\boldsymbol{\Sigma}_{0}+\boldsymbol{\Sigma}_{1}\right)^{-1} \\ \boldsymbol{\mu}^{\prime}=\boldsymbol{\mu}_{\mathbf{0}}+\boldsymbol{K}\left(\boldsymbol{\mu}_{\mathbf{1}}-\boldsymbol{\mu}_{\mathbf{0}}\right) \\ \boldsymbol{\Sigma}^{\prime}=\boldsymbol{\Sigma}_{0}+\boldsymbol{K} \boldsymbol{\Sigma}_{0} \end{gathered} K=Σ0(Σ0+Σ1)−1μ′=μ0+K(μ1−μ0)Σ′=Σ0+KΣ0
回到kalman推导
x ˉ k \bar{\boldsymbol{x}}_{k} xˉk 满足如下分布:
N ( x ‾ k , P ‾ k ) = N ( F k x ^ k − 1 + B k u k , F k P ^ k − 1 F k T + Q k ) (2) N\left(\textcolor{blue}{\overline{\boldsymbol{x}}_{k}, \overline{\boldsymbol{P}}_{k}}\right)=N\left(\boldsymbol{F}_{k} \widehat{\boldsymbol{x}}_{k-1}+\boldsymbol{B}_{k} \boldsymbol{u}_{k}, \boldsymbol{F}_{k} \widehat{\boldsymbol{P}}_{k-1} \boldsymbol{F}_{k}^{T}+\boldsymbol{Q}_{k}\right)\tag{2} N(xk,Pk)=N(Fkxk−1+Bkuk,FkPk−1FkT+Qk)(2)
z k \mathbf{z}_{k} zk 满足如下分布:
N ( z k , Σ ) = N ( H k x ‾ k , H k P ‾ k H k T + R k ) (6) N\left(\textcolor{blue}{\mathbf{z}_{k}, \Sigma}\right)=N\left(\boldsymbol{H}_{\boldsymbol{k}} \overline{\boldsymbol{x}}_{\boldsymbol{k}}, \boldsymbol{H}_{k} \overline{\boldsymbol{P}}_{k} \boldsymbol{H}_{k}^{T}+\boldsymbol{R}_{k}\right)\tag{6} N(zk,Σ)=N(Hkxk,HkPkHkT+Rk)(6)
将 x ‾ k \overline{\boldsymbol{x}}_{k} xk 和 z k \boldsymbol{z}_{k} zk 的分布代入上式(高斯分布知识回顾里面的多维空间高斯分布融合公式):
x ^ k = x ‾ k + K ( z k − x ‾ k ) P ^ k = P ‾ k + K P ‾ k \textcolor{blue}{\begin{gathered} \widehat{\boldsymbol{x}}_{k}=\overline{\boldsymbol{x}}_{k}+\boldsymbol{K}\left(\mathbf{z}_{k}-\overline{\boldsymbol{x}}_{k}\right) \\ \widehat{\boldsymbol{P}}_{k}=\overline{\boldsymbol{P}}_{k}+\boldsymbol{K} \overline{\boldsymbol{P}}_{k} \end{gathered}} xk=xk+K(zk−xk)Pk=Pk+KPk
其中, K = P ‾ k ( P ‾ k + Σ ) − 1 \boldsymbol{K}=\overline{\boldsymbol{P}}_{k}\left(\overline{\boldsymbol{P}}_{k}+\boldsymbol{\Sigma}\right)^{-1} K=Pk(Pk+Σ)−1 为卡尔曼增益。
以上为根据历史状态和观测量, 估计当前位置和速度状态的过程。
当系统为线性马尔可夫系统时,可以通过Kalman Filter来求解融合问题。
{ x ‾ k = F k x ^ k − 1 + B k u k + w k z k = H k x ‾ k + v k k = 1 , 2 , ⋯ , N (7) \left\{\begin{array}{c} \overline{\boldsymbol{x}}_{\boldsymbol{k}}=\boldsymbol{F}_{k} \widehat{\boldsymbol{x}}_{k-1}+\boldsymbol{B}_{k} \boldsymbol{u}_{k}+\boldsymbol{w}_{k} \\ \boldsymbol{z}_{k}=\boldsymbol{H}_{k} \overline{\boldsymbol{x}}_{\boldsymbol{k}}+\boldsymbol{v}_{k} \end{array} \quad k=1,2, \cdots, N\right.\tag{7} { xk=Fkxk−1+Bkuk+wkzk=Hkxk+vkk=1,2,⋯,N(7)
由状态转移方程可得: P ( x ‾ k ∣ x 0 , u 1 : k , z 1 : k − 1 ) = N ( F k x ^ k − 1 + B k u k , F k P ^ k − 1 F k T + Q k ) P\left(\overline{\boldsymbol{x}}_{\boldsymbol{k}} \mid \boldsymbol{x}_{0}, \boldsymbol{u}_{1: k}, \boldsymbol{z}_{1: k-1}\right)=N\left(\boldsymbol{F}_{k} \widehat{\boldsymbol{x}}_{k-1}+\boldsymbol{B}_{k} \boldsymbol{u}_{k}, \boldsymbol{F}_{k} \widehat{\boldsymbol{P}}_{k-1} \boldsymbol{F}_{k}^{T}+\boldsymbol{Q}_{k}\right) P(xk∣x0,u1:k,z1:k−1)=N(Fkxk−1+Bkuk,FkPk−1FkT+Qk)
由观测方程可得: P ( z k ∣ x ‾ k ) = N ( H k x ‾ k , H k P ‾ k H k T + R k ) P\left(\boldsymbol{z}_{k} \mid \overline{\boldsymbol{x}}_{\boldsymbol{k}}\right)=N\left(\boldsymbol{H}_{k} \overline{\boldsymbol{x}}_{\boldsymbol{k}}, \boldsymbol{H}_{k} \overline{\boldsymbol{P}}_{k} \boldsymbol{H}_{k}^{T}+\boldsymbol{R}_{k}\right) P(zk∣xk)=N(Hkxk,HkPkHkT+Rk)
注:
- x ^ k − 1 \widehat{\boldsymbol{x}}_{k-1} xk−1 表示 k − 1 k-1 k−1 时刻系统状态的后验状态;
- P ^ k − 1 \widehat{\boldsymbol{P}}_{k-1} Pk−1 表示对应状态的后验方差;
- Q \boldsymbol{Q} Q 和 R \boldsymbol{R} R 分别 表示状态和观测噪声。
根据贝叶斯法则 P ( x k ∣ x 0 , z 1 : k ) ∝ P ( z k ∣ x k ) P ( x k ∣ x 0 , z 1 : k − 1 ) P\left(\boldsymbol{x}_{k} \mid \boldsymbol{x}_{0}, \boldsymbol{z}_{1: k}\right) \propto P\left(\boldsymbol{z}_{k} \mid \boldsymbol{x}_{k}\right) P\left(\boldsymbol{x}_{k} \mid \boldsymbol{x}_{0}, \boldsymbol{z}_{1: k-1}\right) P(xk∣x0,z1:k)∝P(zk∣xk)P(xk∣x0,z1:k−1), 将 P ( x ‾ k ∣ x 0 , u 1 : k , z 1 : k − 1 ) P\left(\overline{\boldsymbol{x}}_{\boldsymbol{k}} \mid \boldsymbol{x}_{0}, \boldsymbol{u}_{1: k}, \boldsymbol{z}_{1: k-1}\right) P(xk∣x0,u1:k,z1:k−1) 和 P ( z k ∣ x ‾ k ) P\left(\mathbf{z}_{k} \mid \overline{\boldsymbol{x}}_{\boldsymbol{k}}\right) P(zk∣xk) 相乘, 得:
N ( x ^ k , P ^ k ) = N ( H k x ‾ k , H k P ‾ k H k T + Q k ) N ( F k x ^ k − 1 + B k u k , F k P ^ k − 1 F k T + R k ) N\left(\widehat{\boldsymbol{x}}_{k}, \widehat{\boldsymbol{P}}_{k}\right)=N\left(\boldsymbol{H}_{k} \overline{\boldsymbol{x}}_{\boldsymbol{k}}, \boldsymbol{H}_{k} \overline{\boldsymbol{P}}_{k} \boldsymbol{H}_{k}^{T}+\boldsymbol{Q}_{k}\right) N\left(\boldsymbol{F}_{k} \widehat{\boldsymbol{x}}_{k-1}+\boldsymbol{B}_{k} \boldsymbol{u}_{k}, \boldsymbol{F}_{k} \widehat{\boldsymbol{P}}_{k-1} \boldsymbol{F}_{k}^{T}+\boldsymbol{R}_{k}\right) N(xk,Pk)=N(Hkxk,HkPkHkT+Qk)N(Fkxk−1+Bkuk,FkPk−1FkT+Rk)
由此可得, 后验分布 N ( x ^ k , P ^ k ) N\left(\widehat{\boldsymbol{x}}_{k}, \widehat{\boldsymbol{P}}_{k}\right) N(xk,Pk) 的均值和协方差矩阵:
x ^ k = x ‾ k + K ( z k − H k x ‾ k ) P ^ k = ( I − K H k ) P ‾ k \textcolor{blue}{\begin{gathered} \widehat{\boldsymbol{x}}_{k}=\overline{\boldsymbol{x}}_{k}+\boldsymbol{K}\left(\mathbf{z}_{k}-\boldsymbol{H}_{k} \overline{\boldsymbol{x}}_{k}\right) \\ \widehat{\boldsymbol{P}}_{k}=\left(I-\boldsymbol{K} \boldsymbol{H}_{k}\right) \overline{\boldsymbol{P}}_{k} \end{gathered}} xk=xk+K(zk−Hkxk)Pk=(I−KHk)Pk
其中, K = P ‾ k H k T ( H k P ‾ k H k T + Q k ) − 1 \boldsymbol{K}=\overline{\boldsymbol{P}}_{k} \boldsymbol{H}_{k}^{T}\left(\boldsymbol{H}_{k} \overline{\boldsymbol{P}}_{k} \boldsymbol{H}_{k}^{T}+\boldsymbol{Q}_{k}\right)^{-1} K=PkHkT(HkPkHkT+Qk)−1 为卡尔曼增益。
3.总结
状态估计问题建模为:
P ( x k ∣ x 0 , z 1 : k ) ∝ P ( z k ∣ x k ) P ( x k ∣ x k − 1 ) P\left(\boldsymbol{x}_{k} \mid \boldsymbol{x}_{0}, \boldsymbol{z}_{1: k}\right) \propto P\left(\mathbf{z}_{k} \mid \boldsymbol{x}_{k}\right) P\left(\boldsymbol{x}_{k} \mid \boldsymbol{x}_{k-1}\right) P(xk∣x0,z1:k)∝P(zk∣xk)P(xk∣xk−1)
其中:
- P ( z k ∣ x k ) P\left(\mathbf{z}_{k} \mid \boldsymbol{x}_{k}\right) P(zk∣xk) 为似然项,可由观测方程给出
- P ( x k ∣ x k − 1 ) P\left(\boldsymbol{x}_{k} \mid \boldsymbol{x}_{k-1}\right) P(xk∣xk−1) 为先验项,可通过状态转移方程推导得到
一句话总结就是贝叶斯法则+高斯融合:根据贝叶斯法则有,后验估计 ∝ \propto ∝ 似然 * 先验 ,参考链接;然后根据假设(误差服从高斯分布),通过高斯分布的性质,将 似然项高斯分布 和 先验项高斯分布 相乘就得到了后验估计的分布。
边栏推荐
猜你喜欢

视频内容生产与消费创新

正则表达式(正则匹配)

屏幕显示技术进化史

3.10 haas506 2.0 development tutorial example TFT
![Delete duplicate elements in the sorting linked list ii[unified operation of linked list nodes --dummyhead]](/img/dd/7df8f11333125290b4b30183cfff64.png)
Delete duplicate elements in the sorting linked list ii[unified operation of linked list nodes --dummyhead]

详解单例模式

充值满赠,IM+RTC+X 全通信服务「回馈季」开启

How to seamlessly transition from traditional microservice framework to service grid ASM

PC wechat multi open

Electronic components bidding and purchasing Mall: optimize traditional purchasing business and speed up enterprise digital upgrading
随机推荐
「经验」爬虫在工作中的实战应用『理论篇』
Go Redis连接池
Construction and practice of full stack code test coverage and use case discovery system
Glacier teacher's book
Swin-transformer --relative positional Bias
联想YOGA 27 2022,超强配置全面升级
What if icloud photos cannot be uploaded or synchronized?
AI chief architect 10-aica-lanxiang, propeller frame design and core technology
Dlib库实现人脸关键点检测(Opencv实现)
ForkJoinPool
开发那些事儿:Linux系统中如何安装离线版本MySQL?
Coding officially entered Tencent conference application market!
Countdowncatch and completabilefuture and cyclicbarrier
How does rust implement dependency injection?
How to do a good job in software system demand research? Seven weapons make it easy for you to do it
com.alibaba.fastjson.JSONObject # toJSONString 消除循环引用
Cloud Native Landing Practice Using rainbond for extension dimension information
一套十万级TPS的IM综合消息系统的架构实践与思考
期货怎么开户安全些?现在哪些期货公司靠谱些?
Full recharge, im+rtc+x full communication service "feedback season" starts