当前位置:网站首页>奇技淫巧-位运算
奇技淫巧-位运算
2022-08-02 14:10:00 【老顽固也可爱】
位运算概览
| 符号 | 描述 | 运算规则 | 例子 |
|---|---|---|---|
| & | 与 | 两个位都为1时,结果才为1,否则结果为0 | 3&5=0011&0101=0001=1 |
 | 或 | 参加运算的两个对象只要有一个为1,其值为1。 | 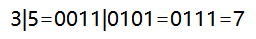 |
| ^ | 异或 | 两个位相同为0,相异为1 | 3^ 5=0011^0101=1001=9 |
| ~ | 取反 | 0变1,1变0 | |
| << | 左移 | 各二进位全部左移若干位,高位丢弃,低位补0 | 1010 1110<<2=1011 1000 |
| >> | 右移 | 各二进位全部右移若干位,对无符号数,高位补0,有符号数,各编译器处理方法不一样,有的补符号位(算术右移),有的补0(逻辑右移) |
注意:负数按补码形式参加按位与运算。
1.与运算符(&)
| 与运算的用途 | |
|---|---|
| 取一个数的指定位 | 比如取数 X=1010 1110 的低4位,只需要另找一个数Y,令Y的低4位为1,其余位为0,即Y=0000 1111,然后将X与Y进行按位与运算(X&Y=0000 1110)即可得到X的指定位。 |
| 清零 | 如果想将一个单元清零,即使其全部二进制位为0,只要与一个各位都为零的数值相与,结果为零。 |
| 判断奇偶 | 只要根据最未位是0还是1来决定,为0就是偶数,为1就是奇数。因此可以用if ((a&1)==0)代替if (a%2 == 0)来判断a是不是偶数。 |
2.或运算符(|)
| 或运算的用途 | |
|---|---|
| 常用来对一个数据的某些位设置为1 | 比如将数 X=1010 1110 的低4位设置为1,只需要另找一个数Y,令Y的低4位为1,其余位为0,即Y=0000 1111,然后将X与Y进行按位或运算(X |
3.异或运算符(^)
异或的几条性质:
1、交换律
2、结合律 (a^ b)^ c == a^ (b^c)
3、对于任何数x,都有 xx=0,x0=x
4、自反性: a^ b^ b=a^0=a;
| 异或运算的用途 | |
|---|---|
| 翻转指定位 | 比如将数 X=1010 1110 的低4位进行翻转,只需要另找一个数Y,令Y的低4位为1,其余位为0,即Y=0000 1111,然后将X与Y进行异或运算(X^Y=1010 0001)即可得到。 |
| 与0相异或值不变 | 例如:1010 1110 ^ 0000 0000 = 1010 1110 |
| 交换两个数 | 交换a与b的值,a ^= b;b ^= a; a ^= b; |
void Swap(int& a, int& b)
{
if (a != b)
{
a ^= b;
b ^= a;
a ^= b;
}
}
4.取反运算符 (~)
| 取反运算的用途 | |
|---|---|
| 使一个数的最低位为零 | 使a的最低位为0,可以表示为:a &~ 1。~1的值为 1111 1111 1111 1110,再按"与"运算,最低位一定为0。因为“ ~”运算符的优先级比算术运算符、关系运算符、逻辑运算符和其他运算符都高。 |
5.左移运算符(<<)
定义:将一个运算对象的各二进制位全部左移若干位(左边的二进制位丢弃,右边补0)。
若左移时舍弃的高位不包含1,则每左移一位,相当于该数乘以2。
6.右移运算符(>>)
定义:将一个数的各二进制位全部右移若干位,正数左补0,负数左补1,右边丢弃。
例如:a=a>>2 将a的二进制位右移2位,左补0 或者 左补1得看被移数是正还是负。
操作数每右移一位,相当于该数除以2。
注意
不同长度的数据进行位运算:如果两个不同长度的数据进行位运算时,系统会将二者按右端对齐,然后进行位运算。
以“与运算”为例说明如下:我们知道在C语言中long型占4个字节,int型占2个字节,如果一个long型数据与一个int型数据进行“与运算“,右端对齐后,左边不足的位依下面三种情况补足:
1)如果整型数据为正数,左边补16个0。
2)如果整型数据为负数,左边补16个1。
3)如果整形数据为无符号数,左边也补16个0。
边栏推荐
- Article pygame drag the implementation of the method
- 2.4G无线小模块CI24R1超低成本
- Golang 垃圾回收机制详解
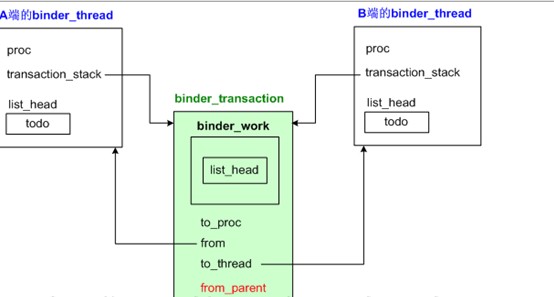
- Binder ServiceManager解析
- What should I do if the Win10 system sets the application identity to automatically prompt for access denied?
- 镜像法求解接地导体空腔电势分布问题
- Mapreduce环境详细搭建和案例实现
- Yolov5 official code reading - prior to transmission
- 设备驱动框架简介
- Win7遇到错误无法正常开机进桌面怎么解决?
猜你喜欢
随机推荐
FP5139电池与适配器供电DC-DC隔离升降压电路反激电路电荷泵电路原理图
jest测试,组件测试
DP1101兼容CC1101是SUB1GHz无线收发芯片应用于智能家居
Compilation error D8021: Invalid numeric argument '/Wextra' cl command line error d8021 invalid numeric argument '/Wextra'
vscode镜像
Win10无法连接打印机怎么办?不能使用打印机的解决方法
二叉树创建之层次法入门详解
Win11 keeps popping up User Account Control how to fix it
cmake配置libtorch报错Failed to compute shorthash for libnvrtc.so
LORA芯片ASR6601支持M4内核的远距离传输芯片
pygame图像连续旋转
pygame draw arc
CI24R1小模块2.4G收发模块无线通信低成本兼容si24r1/XN297超低功耗
Please make sure you have the correct access rights and the repository exists.问题解决
pygame拖动条的实现方法
Win10上帝模式干嘛的?Win10怎么开启上帝模式?
FP7128内置MOS降压恒流调光深度0.01%高辉共阳调光方案
The SSE instructions into ARM NEON
FP7195芯片PWM转模拟调光至0.1%低亮度时恒流一致性的控制原理
Use libcurl to upload the image of Opencv Mat to the file server, based on two methods of post request and ftp protocol