当前位置:网站首页>二叉树创建之层次法入门详解
二叉树创建之层次法入门详解
2022-08-02 14:10:00 【杨老头软工】
一、引言
前面已经给出了先序法创建二叉树的两种方法,分别是非递归的方法和递归方法,本文将给出了C语言版本的层次法创建二叉树的算法。所谓的层次法其实就是按照二叉树中结点所在的“层”进行遍历,每一层遍历的规则是从左到右。因此层次遍历其实就是按照完全二叉树中结点的编号次序进行遍历的,但是二叉树不一定都是完全二叉树,因此涉及到虚拟的补充成完全二叉树,然后再进行层次遍历。
所使用的示例二叉树如下图所示。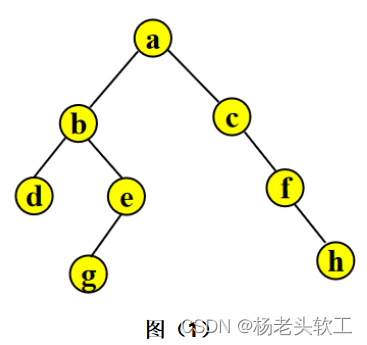
二、二叉树的创建-层次法
1、结点编号规则
层次法创建二叉树,仍旧需要把扩充二叉树。但是此处不同于先序法的扩充的是,需要按照完全二叉树的模式扩充结点。补齐这些结点的目的是为了记录完全二叉树的结点编号而已,因此事实上并不需要真的补齐缺的结点,只需要记住二叉树上所有的结点在完全二叉树上结点的编号即可。
此时,图(1)中结点的编号如下(从1开始):
2、算法的基本思路:
首先创建一个数组S,用于存储二叉树上全部的结点。
之后开始依次读入结点数据,具体做法是一次同时读入某个结点的编号i和数据data,以此创建结点,并把该结点放到数组S的下标为i的位置。接着根据i/2来确定其双亲在S中的下标,且根据i是否被2整除来确定结点i是j的左子树还是右子树。
3、算法的具体实现:
#include"stdio.h"
#include"malloc.h"
#define CHAR
#define MAX_NODE 100
#ifdef CHAR
typedef char datatype;
#else
typedef int datatype;
#endif
typedef struct node
{
datatype data;
struct node *Lchild;
struct node *Rchild;
}BiTree;
BiTree *CreateBiTreeLevel( void )
{
BiTree *T, *p, *s[MAX_NODE];
datatype data;
int i, j;
T = NULL;
while ( 1 )
{
printf( " 输入结点编号( 0 则终止输入 ): " );
scanf( "%d", &i );
if( i == 0 )
break;
else
{
#ifdef CHAR
getchar();//过滤输入结点编号后面的换行符
printf( " 请输入结点数据(字符):" );
scanf( "%c",&data );
getchar();//过滤结点数据后面的换行符
#else
printf( " 请输入结点数据(整数):" );
scanf( "%d",&data );
#endif
//创建结点,并把data存入该结点,同时把该结点的左右子树置空
p = ( BiTree * )malloc( sizeof(BiTree) ) ;
p->data = data ;
p->Lchild = NULL;
p->Rchild = NULL;
s[i] = p ;
if( i == 1 ) //编号为1的结点是树根
T = p ;
else//找新加入结点的双亲
{
j = i / 2; // j是i的双亲结点编号
if( i % 2 == 0 )
{
s[j]->Lchild = p;//左子树
//下面的输出是为了检验结点的位置是否跟预期相符。
#ifdef CHAR
printf( " %c 是 %c 的左子树\n", p->data, s[j]->data );
#else
printf( " %d 是 %d 的左子树\n", p->data, s[j]->data );
#endif
}
else
{
s[j]->Rchild = p;//右子树
#ifdef CHAR
printf( " %c 是 %c 的右子树\n", p->data, s[j]->data );
#else
printf( " %d 是 %d 的右子树\n", p->data, s[j]->data );
#endif
}
}
}
}
return( T );
}
int main()
{
BiTree *T = CreateBiTreeLevel( );
return 0;
}
4、运行结果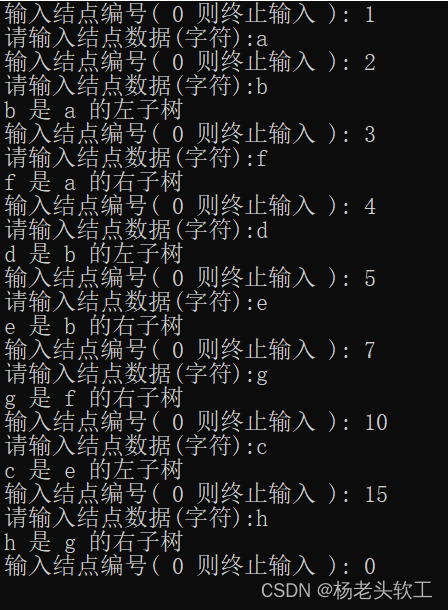
边栏推荐
- Win11 keeps popping up User Account Control how to fix it
- 推开机电的大门《电路》(三):说说不一样的电阻与电导
- DP1101兼容CC1101是SUB1GHz无线收发芯片应用于智能家居
- win10任务栏不合并图标如何设置
- vscode镜像
- ASR6601牛羊定位器芯片GPS国内首颗支持LoRa的LPWAN SoC
- 关于c语言的调试技巧
- 使用libcurl将Opencv Mat的图像上传到文件服务器,基于post请求和ftp协议两种方法
- A clean start Windows 7?How to load only the basic service start Windows 7 system
- 为android系统添加产品的过程
猜你喜欢
How to update Win11 sound card driver?Win11 sound card driver update method

win10系统更新错误代码0x80244022怎么办
蓝牙温度检测系统(基于BT08-B蓝牙模块)
Mysql connection error solution
ARMv8虚拟化
win10任务栏不合并图标如何设置
SQL的通用语法和使用说明(图文)

FP5207电池升压 5V9V12V24V36V42V大功率方案
What should I do if the Win10 system sets the application identity to automatically prompt for access denied?

Makefile容易犯错的语法
随机推荐
实战美团Nuxt +Vue全家桶,服务端渲染,邮箱验证,passport鉴权服务,地图API引用,mongodb,redis等技术点
TCP三次握手、四次挥手
LORA芯片ASR6601支持M4内核的远距离传输芯片
推开机电的大门《电路》(一):电压,电流,参考方向
基于矩阵计算的线性回归分析方程中系数的估计
【STM32学习1】基础知识与概念明晰
Win10 cannot directly use photo viewer to open the picture
Win10电脑需要安装杀毒软件吗?
win10怎么设置不睡眠熄屏?win10设置永不睡眠的方法
图像配置分类及名词解释
2021-10-14
【我的电赛日记(三)】STM32学习笔记与要点总结
Impressions of Embrace Jetpack
In-depth understanding of Golang's Map
jest test, component test
Configure clangd for vscode
ASR6601牛羊定位器芯片GPS国内首颗支持LoRa的LPWAN SoC
win10任务栏不合并图标如何设置
Article pygame drag the implementation of the method
使用 腾讯云搭建一个个人博客