当前位置:网站首页>ICML 2022 | meta proposes a robust multi-objective Bayesian optimization method to effectively deal with input noise
ICML 2022 | meta proposes a robust multi-objective Bayesian optimization method to effectively deal with input noise
2022-07-05 17:27:00 【PaperWeekly】

author | Yangzequn
Company | Renmin University of China
Research direction | Multimodal learning

Paper title :
Robust Multi-Objective Bayesian Optimization Under Input Noise
Thesis link :
https://arxiv.org/abs/2202.07549
Project links :
https://github.com/facebookresearch/robust_mobo
This article is about facebook Published in ICML 2022 A piece of work for , It theoretically analyzes the multi-objective Bayesian Optimization with input noise .

introduction
This paper deals with the input noise problem of multi-objective optimization , Combined with Bayesian Optimization and Pareto optimization, the global multi-objective VaR is designed and optimized , To solve the problem of black box constraint sensitive to input noise . Bayesian optimization by adjusting design parameters , Black box performance indicators with high evaluation cost can be optimized . Although many methods have been proposed to optimize a single target under input noise , However, there is still a lack of methods to solve the practical problem that multiple targets are sensitive to input disturbances .
In this work , The author proposes the first robust multi-objective Bayesian optimization method to deal with input noise . The author formalizes the goal as a risk measure to optimize an uncertain goal , That is, multivariable value at risk (MVaR). Due to direct optimization MVaR In many cases, it is computationally infeasible , The author proposes an extensible 、 A theory based approach to use random scales to optimize MVaR. Experimentally speaking , This method is significantly better than other methods in data set , And effectively realize the optimal Luban design .
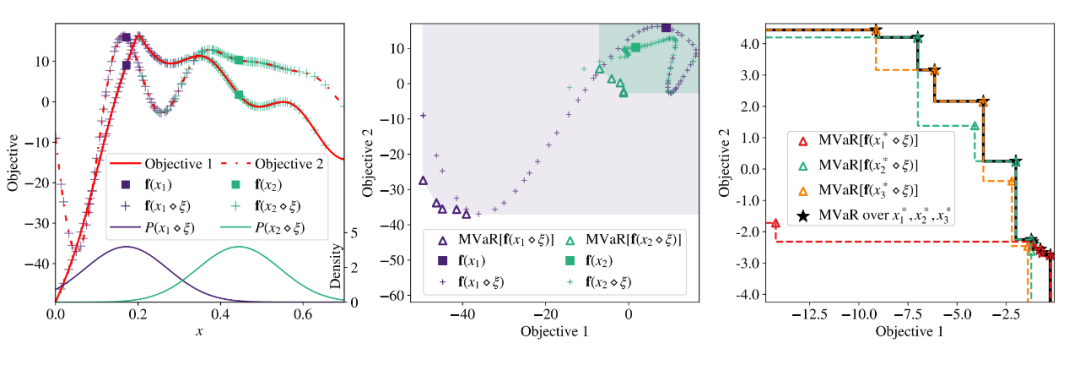
▲ chart 1: The simple data set shows that the optimal value of multi-objective optimization of non robust design is sensitive to input noise , And it gives a demonstration of the selection of the best set .
Here, through the graph 1 Let's sort out the questions raised by the author : On the left , Non robust design ( violet ) And robust design ( green ) The nominal value of is represented by a square . The plus sign indicates the target value of each design under zero mean Gaussian input noise , The standard deviation is 0.1. You can see , Although non robust design may obtain locally better results , But its instability under input disturbance , Easy to lead to worse performance ; And robust design The result of is small for the input disturbance , Insensitive to input noise .
The graph in the middle is for non robust and robust design MVaR Description of the set , The triangle represents the distribution of input noise , Every design MVaR Discrete approximation of sets . Without considering noise , violet A square can correspond to a better value ; But after being disturbed, its risk (MVaR) more , It is difficult to be robust to input noise . Therefore, multivariable risk value can be used to characterize the stability of the solution . The right figure is a description of the selection strategies of different risk sets , The hypothetical method gives MVaR aggregate , The optimal set of risks is different objectives MVaR The best set on the union of sets .

background
Multi objective optimization makes trade-offs between multiple black box functions , The goal is to identify the Pareto boundary of the optimal trade-off and the Pareto set of the corresponding optimal design . Consider maximizing black box functions : among , Is the number of targets , Is the tight search space . The above definition can lead to the definition of Pareto domination and Pareto boundary . If the vector Pareto dominates , Write it down as , If and only if also Satisfy .
Pareto is the best (Pareto optimality) It is a state that cannot be improved , It is impossible to improve some individuals or preference criteria without damaging any other individuals or criteria . If there is Pareto optimal improvement in a state , Then it is called Pareto dominated . If a state is not dominated by Pareto , Then it is called Pareto optimal or Pareto efficient , In optimization problems, it can be regarded as the best . The set of such best points is called Pareto boundary . As you can see from the picture below ,A and B Is the point on the Pareto boundary , They are all for C The domination of .
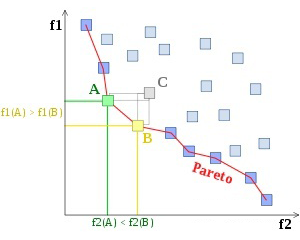
▲ chart 2: Here is an example of Pareto boundary . Points in the set represent feasible choices , Here, it is considered that a smaller value is better , The red line represents the Pareto boundary , The sample points above are Pareto efficient . spot C At the same time A Sum point B control , So it is not on the Pareto boundary . spot A Sum point B Not strictly controlled by any other point , So it's on the boundary .
Defined here Pareto boundary of :
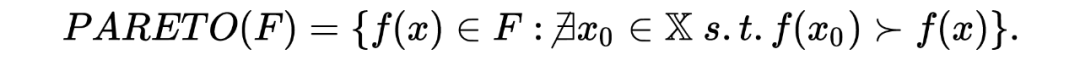
if PARETO The elements in satisfy the additional constraints of the black box , Then the corresponding optimal design set is considered as Pareto boundary . Then , By defining measures ( Hypervolume and hypervolume increment ) To measure the quality of different Pareto boundaries , That is, the measure value of the region contained within the Pareto boundary .

Method
First of all, we need to define the risk . Because the expected risk measurement may not always be consistent with the real robustness goal , Therefore, probabilistic risk analysis is used here , And get the following definition :
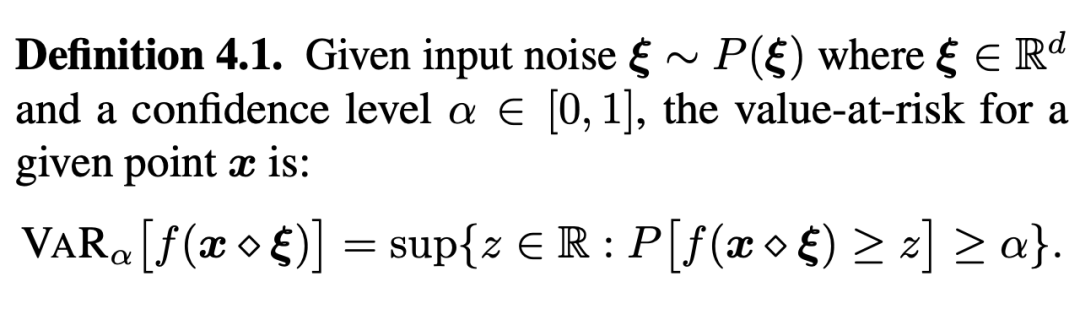
The definition of value at risk is given above , It gets in the noise A lower bound of , bring At least The probability of falling is greater than In the domain of , And call it probabilistic risk , To measure the noise of a single target .
And for Multivariate Value-at-Risk(MVaR) for , be-all All targets are evaluated in the same noisy samples . The author designs on the boundary of multiple targets, which is the Pareto boundary of different targets , It can be written in the following form :
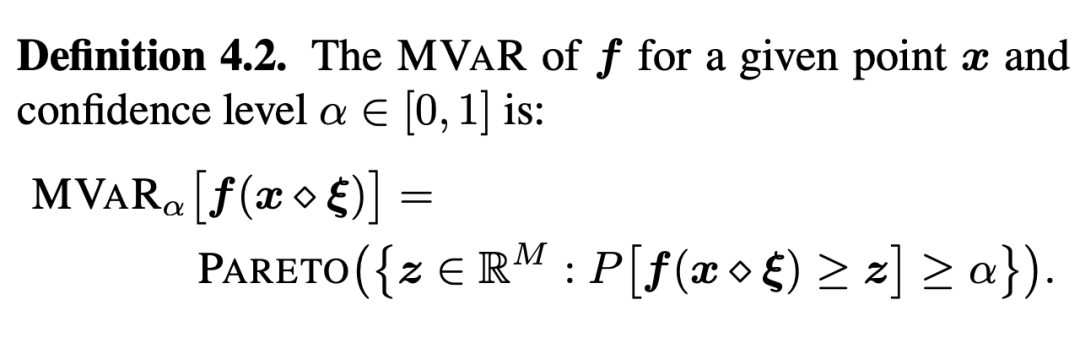
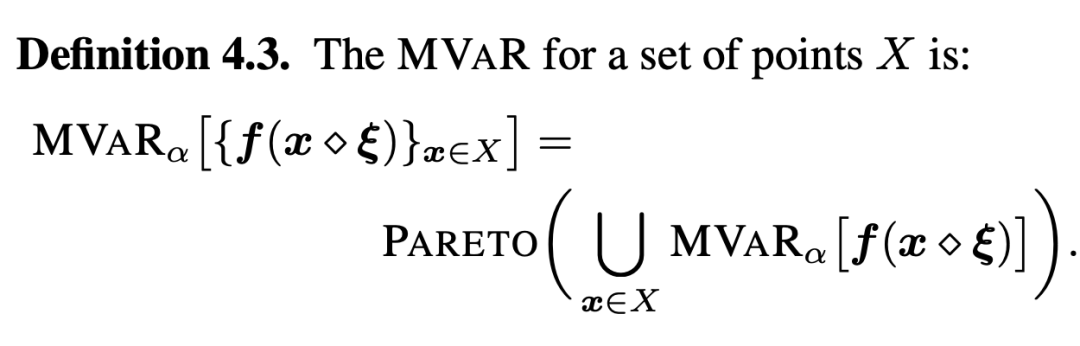
thus , It defines the global risk across the design space , Is to adopt a series of points ( See the picture 1 The triangle of ), Robust approximation of Pareto boundary in multi-objective situation , This is also one of the important contributions of this article .
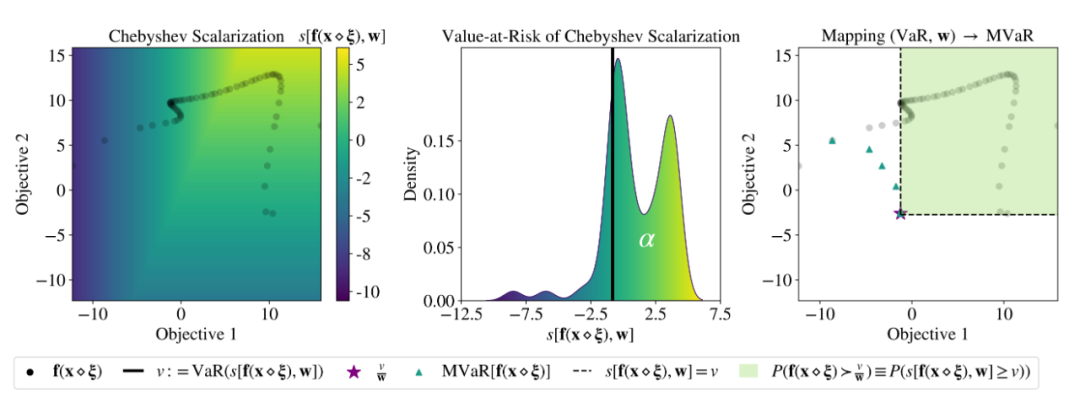
▲ chart 3: For Graphs 1 in toy Data MVaR The building process of
This paper proposes MARS Method , By introducing Chebyshev scaling VaR and MVaR The relationship between , And can be used to MVaR Set to estimate . Here's the picture 3 It's the graph 1 Simple data MVaR The process of building a collection , The black dot in the left figure indicates that the standard deviation is 0.1, The mean for 0 The function value of Gaussian input disturbance , The background is an outline showing Chebyshev scaling values across the target space . The graph in the middle shows the probability density and of Chebyshev scaling Chebyshev scaled var , The probability mass to the right of the black line is equal to . The right figure shows the relationship constructed by the theorem proved in the text , take VaR Mapping to MVaR in , The green triangle represents MVaR Discrete approximation of sets .

The main result
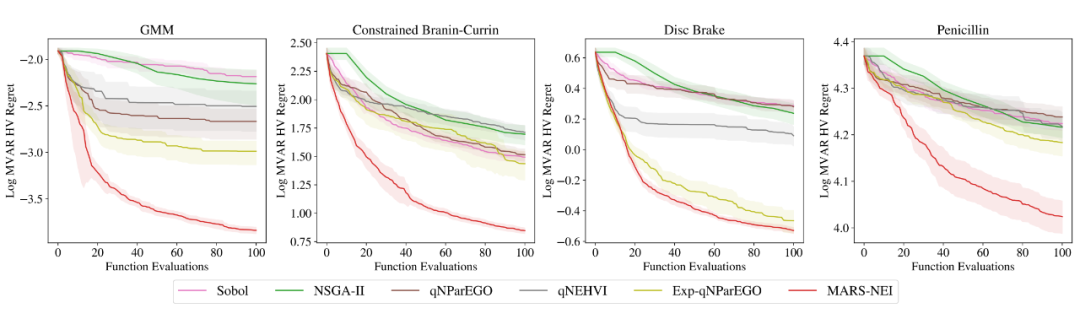
▲ chart 4: stay 4 Evaluation on different noise data sets
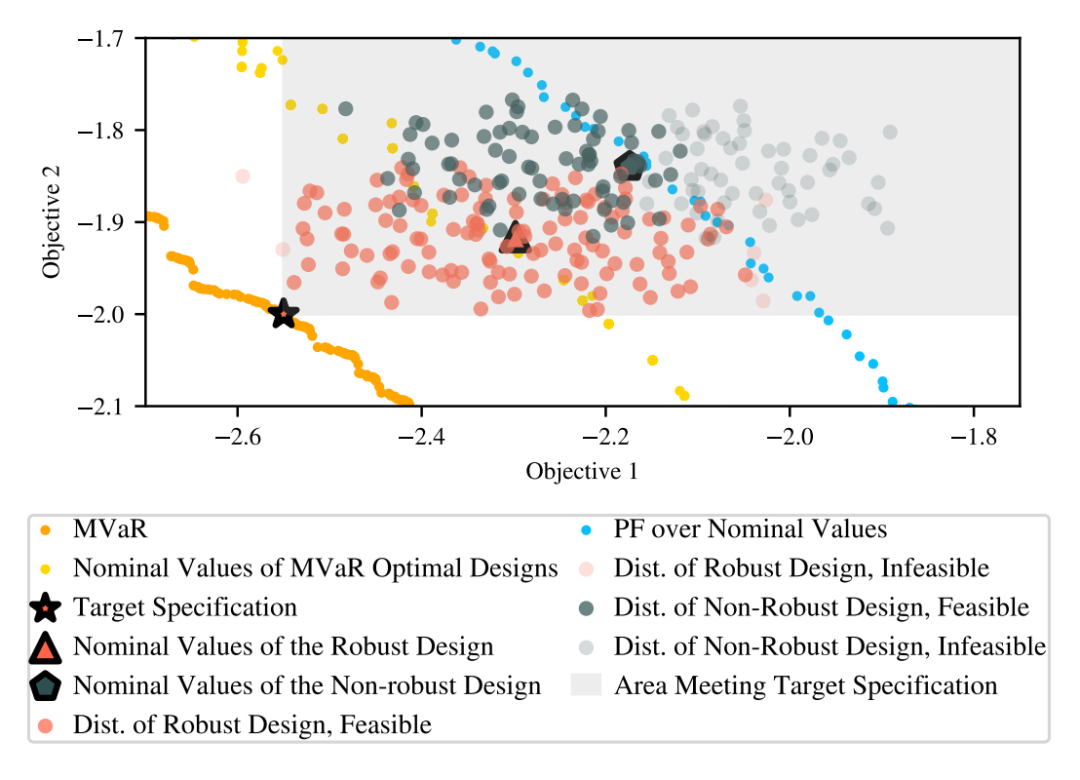
▲ chart 5: Although non robust design in noiseless targets (Nominal Values) It is feasible , But it is located near the boundary of the feasible area in the design space , In the case of input disturbance, the constraint in the black box will be violated , Make the obtained solution infeasible
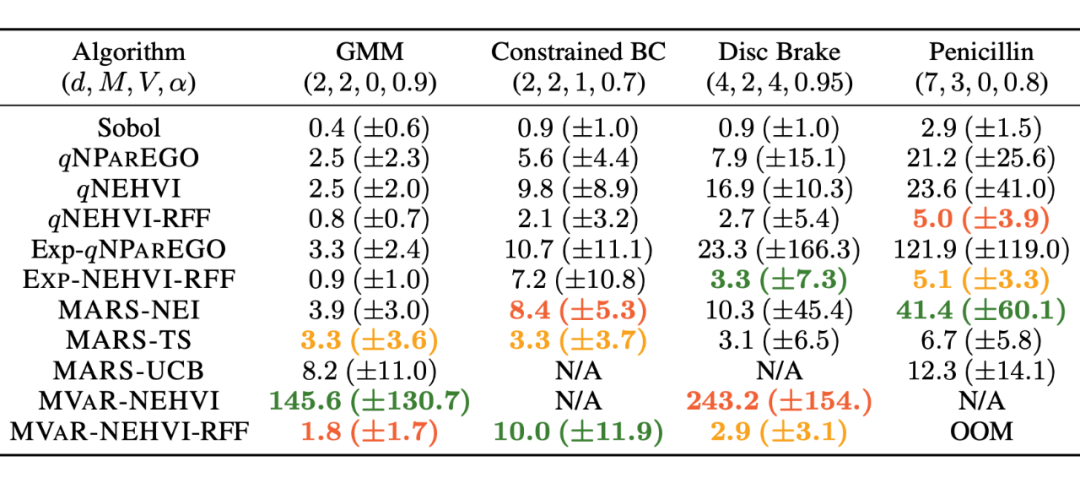
▲ surface 1: The running time of each iteration of Bayesian Optimization of different algorithms
chart 4 It shows the changes with the training process , The performance of each algorithm , The overall situation is adopted here MVaR And design MVaR The gap between HV The logarithm of is used as the evaluation index , It can explain the design MVaR Can we approach the overall situation . Under the intervention of input noise , The non robust method is significantly weaker than the robust method , The author's method is due to other comparative methods . chart 5 It shows that in the real data set , Choose the benefits of robust design and non robust design respectively . It can be seen here that through MVaR The learned design is closer to the target value , The solution obtained by non robust design is more likely to fall into the infeasible region . surface 1 It shows MARS-based The advantages of the method in running time .

Summary and reflection
In this work , The author combines the properties of Bayesian Optimization and multi-objective fusion , The input noise is analyzed from the distribution level , It is designed MVaR Risk and find Pareto optimality of multi-objective risk , A good combination of the characteristics of the two methods , The idea is relatively simple and reasonable . For the optimization of other multi-source targets , For example, multimodal 、 Multiple perspectives 、 For multi task learning , This method guides us to start from the perspective of data disturbance risk , To analyze the potential input noise problem in the method .
meanwhile , Because the method is simple but difficult to express intuitively , The author used less space to achieve a clear exposition of the method , Then, through a lot of foreshadowing, it clearly expounds the background and main contributions of the article , A large number of proofs are given in the appendix to illustrate the correctness of the lemma . meanwhile , The author explains the main problems and methods through only two images , It clearly shows the robustness problem in the multi-objective situation .
At the method level , This method uses a series of points to estimate the distribution boundary , It is based on anchor Methods , The idea of estimating data distribution through anchor selection is similar , The two describe the distribution boundary and the distribution situation respectively . Later, for noise ( Input noise 、 Label noise ) In this case, we should think deeply about the relationship between the two .
Read more

# cast draft through Avenue #
Let your words be seen by more people
How to make more high-quality content reach the reader group in a shorter path , How about reducing the cost of finding quality content for readers ? The answer is : People you don't know .
There are always people you don't know , Know what you want to know .PaperWeekly Maybe it could be a bridge , Push different backgrounds 、 Scholars and academic inspiration in different directions collide with each other , There are more possibilities .
PaperWeekly Encourage university laboratories or individuals to , Share all kinds of quality content on our platform , It can be Interpretation of the latest paper , It can also be Analysis of academic hot spots 、 Scientific research experience or Competition experience explanation etc. . We have only one purpose , Let knowledge really flow .
The basic requirements of the manuscript :
• The article is really personal Original works , Not published in public channels , For example, articles published or to be published on other platforms , Please clearly mark
• It is suggested that markdown Format writing , The pictures are sent as attachments , The picture should be clear , No copyright issues
• PaperWeekly Respect the right of authorship , And will be adopted for each original first manuscript , Provide Competitive remuneration in the industry , Specifically, according to the amount of reading and the quality of the article, the ladder system is used for settlement
Contribution channel :
• Send email :[email protected]
• Please note your immediate contact information ( WeChat ), So that we can contact the author as soon as we choose the manuscript
• You can also directly add Xiaobian wechat (pwbot02) Quick contribution , remarks : full name - contribute

△ Long press add PaperWeekly Small make up
Now? , stay 「 You know 」 We can also be found
Go to Zhihu home page and search 「PaperWeekly」
Click on 「 Focus on 」 Subscribe to our column
·

边栏推荐
- Is it safe for qiniu business school to open a stock account? Is it reliable?
- 漫画:一道数学题引发的血案
- winedt常用快捷键 修改快捷键latex编译按钮
- 北京内推 | 微软亚洲研究院机器学习组招聘NLP/语音合成等方向全职研究员
- CMake教程Step4(安装和测试)
- Rider set the highlighted side of the selected word, remove the warning and suggest highlighting
- 启牛商学院股票开户安全吗?靠谱吗?
- 华为云云原生容器综合竞争力,中国第一!
- The first lesson of EasyX learning
- thinkphp3.2.3
猜你喜欢
一文了解MySQL事务隔离级别

Embedded UC (UNIX System Advanced Programming) -1
项目引入jar从私服Nexus 拉去遇到的一个问题

The survey shows that the failure rate of traditional data security tools in the face of blackmail software attacks is as high as 60%
兰空图床苹果快捷指令
Complete solution instance of Oracle shrink table space
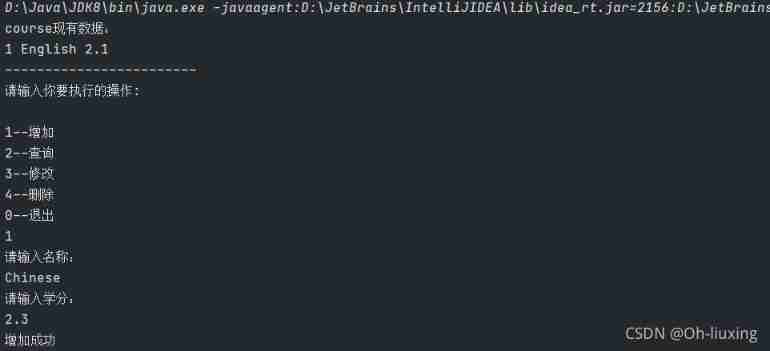
Use JDBC technology and MySQL database management system to realize the function of course management, including adding, modifying, querying and deleting course information.
thinkphp模板的使用

机器学习01:绪论
【jmeter】jmeter脚本高级写法:接口自动化脚本内全部为变量,参数(参数可jenkins配置),函数等实现完整业务流测试
随机推荐
High number | summary of calculation methods of volume of rotating body, double integral calculation of volume of rotating body
忽米沄析:工业互联网标识解析与企业信息系统的融合应用
Matery主题自定义(一)黑夜模式
[first lecture on robot coordinate system]
激动人心!2022开放原子全球开源峰会报名火热开启!
漫画:如何实现大整数相乘?(上) 修订版
这个17岁的黑客天才,破解了第一代iPhone!
一口气读懂 IT发展史
WR | 西湖大学鞠峰组揭示微塑料污染对人工湿地菌群与脱氮功能的影响
Wsl2.0 installation
MySQL queries the latest qualified data rows
Cloud security daily 220705: the red hat PHP interpreter has found a vulnerability of executing arbitrary code, which needs to be upgraded as soon as possible
Error in composer installation: no composer lock file present.
Embedded -arm (bare board development) -1
Flow characteristics of kitchen knife, ant sword, ice scorpion and Godzilla
thinkphp3.2.3
[Jianzhi offer] 61 Shunzi in playing cards
Zhang Ping'an: accélérer l'innovation numérique dans le cloud et construire conjointement un écosystème industriel intelligent
Read the basic grammar of C language in one article
Practical example of propeller easydl: automatic scratch recognition of industrial parts