当前位置:网站首页>漫画:如何实现大整数相乘?(上) 修订版
漫画:如何实现大整数相乘?(上) 修订版
2022-07-05 16:51:00 【小灰】
这周一小灰发布的新漫画中,存在两个小问题:
1.对于master定理的第三个条件叙述有误,应该是a+ε,而不是a-ε。
2.把分治法的T(n)和T(n/2)的关系带入master定理的第一个条件,计算ε值的过程有误。
本次修改了这两个问题,非常感谢小伙伴们的指正。
前一段时间,小灰发布了一篇有关大整数相加的漫画,没看过的小伙伴可以先看一看:
那么,大整数相乘又是如何实现的呢?
起初,小灰认为只要按照大整数相加的思路稍微做一下变形,就可以轻松实现大整数相乘。但是随着深入的学习,小灰才发现事情并没有那么简单......
————— 第二天 —————
怎样列出这个乘法竖式呢?以 93281 X 2034 为例,竖式如下:
在程序中,我们可以利用int型数组,把两个大整数按位进行存储,再把数组中的元素像小学竖式那样逐个进行计算。
这个乘法竖式的计算过程可以大体分为两步:
1.整数B的每一个数位和整数A所有数位依次相乘,得到中间结果。
2.所有中间结果相加,得到最终结果。
/**
* 大整数求乘积
* @param bigNumberA 大整数A
* @param bigNumberB 大整数B
*/
public static String multiply(String bigNumberA, String bigNumberB) {
//1.把两个大整数用数组逆序存储,数组长度等于两整数长度之和
int lengthA = bigNumberA.length();
int lengthB = bigNumberB.length();
int[] arrayA = new int[lengthA];
for(int i=0; i< lengthA; i++){
arrayA[i] = bigNumberA.charAt(lengthA-1-i) - '0';
}
int[] arrayB = new int[lengthB];
for(int i=0; i< lengthB; i++){
arrayB[i] = bigNumberB.charAt(lengthB-1-i) - '0';
}
//2.构建result数组,数组长度等于两整数长度之和
int[] result = new int[lengthA+lengthB];
//3.嵌套循环,整数B的每一位依次和整数A的所有数位相乘,并把结果累加
for(int i=0;i<lengthB;i++) {
for(int j=0;j<lengthA;j++) {
//整数B的某一位和整数A的某一位相乘
result[i+j] += arrayB[i]*arrayA[j];
//如果result某一位大于10,则进位,进位数量是该位除以10的商
if(result[i+j] >= 10){
result[i+j+1] += result[i+j]/10;
result[i+j] = result[i+j]%10;
}
}
}
//4.把result数组再次逆序并转成String
StringBuilder sb = new StringBuilder();
//是否找到大整数的最高有效位
boolean findFirst = false;
for (int i = result.length - 1; i >= 0; i--) {
if(!findFirst){
if(result[i] == 0){
continue;
}
findFirst = true;
}
sb.append(result[i]);
}
return sb.toString();
}
public static void main(String[] args) {
String x = "3338429042340042304302404";
String y = "12303231";
System.out.println(multiply(x, y));
}————————————
下面,我们的推导会有一些烧脑,请大家坐稳扶好~~
大整数从高位到低位,被平分成了两部分。设整数1的高位部分是A,低位部分是B;整数2的高位部分是C,低位部分是D,那么有如下等式:
如果把大整数的长度抽象为n,那么:
因此,整数1与整数2 的乘积可以写成下面的形式:
如此一来,原本长度为n的大整数的1次乘积,被转化成了长度为n/2的大整数的4次乘积(AC,AD,BC,BD)。
什么是master定理呢?
master定理的英语名称是master theorem,它为许多由分治法得到的递推关系式提供了渐进时间复杂度分析。
设常数a >= 1,b > 1,如果一个算法的整体计算规模 T(n) = a T(n / b) + f(n),那么则有如下规律:
假设两个长度为n的大整数相乘,整体运算规模是T(n) 。
根据刚才得到的结论,两个大整数相乘被拆分成四个较小的乘积:
所以在第一次分治时,T(n)和T(n/2)有如下关系:
T(n) = 4T(n/2) + f(n)
其中f(n)是4个乘积结果相加的运算规模,f(n)的渐进时间复杂度很明显是O(n)。
把这个关系带入到master定理的公式 T(n) = a T(n / b) + f(n) 当中,
此时 a=4, b=2。
此时,把a和b的值,以及f(n)的时间复杂度带入到master定理的第一个规律,也就是下面的规律:
发现正好符合条件。
怎么符合呢?推导过程如下:
所以我们的平均时间复杂度是:
—————END—————
边栏推荐
- Is it safe for qiniu business school to open a stock account? Is it reliable?
- easyNmon使用汇总
- How MySQL uses JSON_ Extract() takes JSON value
- dried food! Semi supervised pre training dialogue model space
- Timestamp strtotime the day before or after the date
- High number | summary of calculation methods of volume of rotating body, double integral calculation of volume of rotating body
- WR | Jufeng group of West Lake University revealed the impact of microplastics pollution on the flora and denitrification function of constructed wetlands
- 国内首家 EMQ 加入亚马逊云科技「初创加速-全球合作伙伴网络计划」
- Etcd 构建高可用Etcd集群
- 【剑指 Offer】62. 圆圈中最后剩下的数字
猜你喜欢
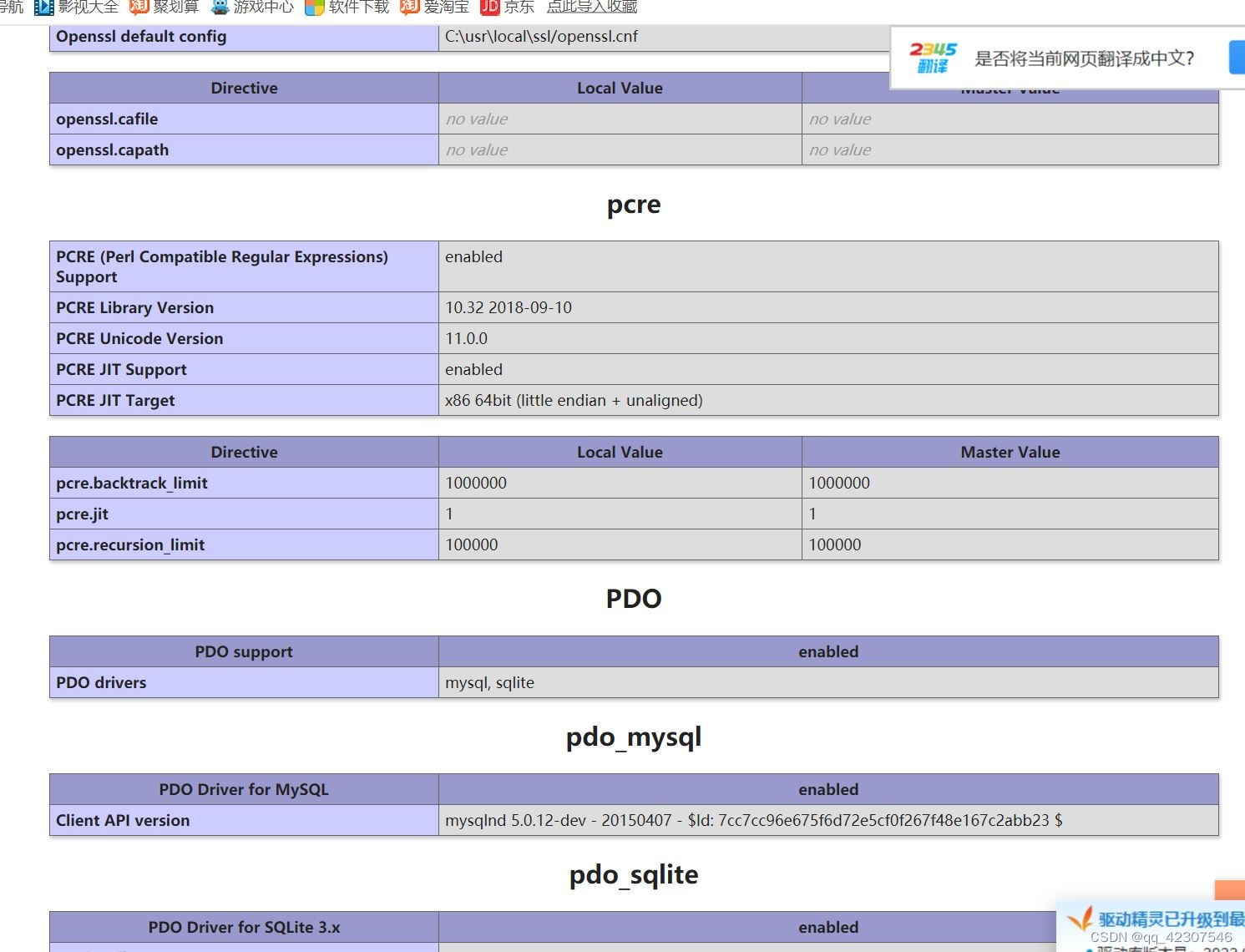
thinkphp3.2.3
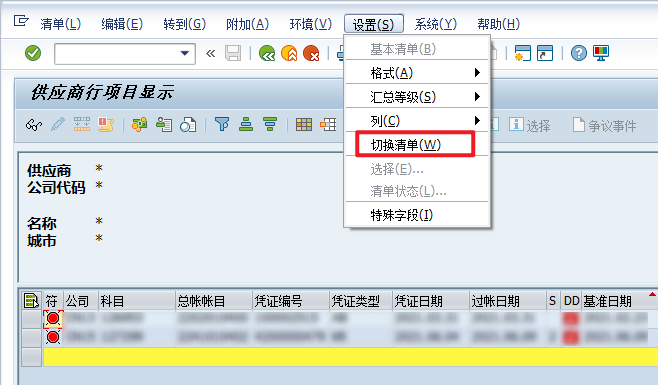
VBA驱动SAP GUI实现办公自动化(二):判断元素是否存在

The second day of learning C language for Asian people
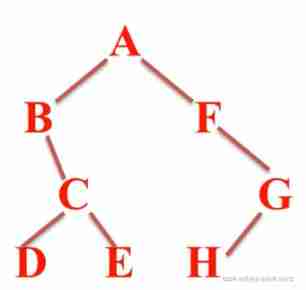
Three traversal methods of binary tree

WR | 西湖大学鞠峰组揭示微塑料污染对人工湿地菌群与脱氮功能的影响

Etcd 构建高可用Etcd集群
Design of electronic clock based on 51 single chip microcomputer
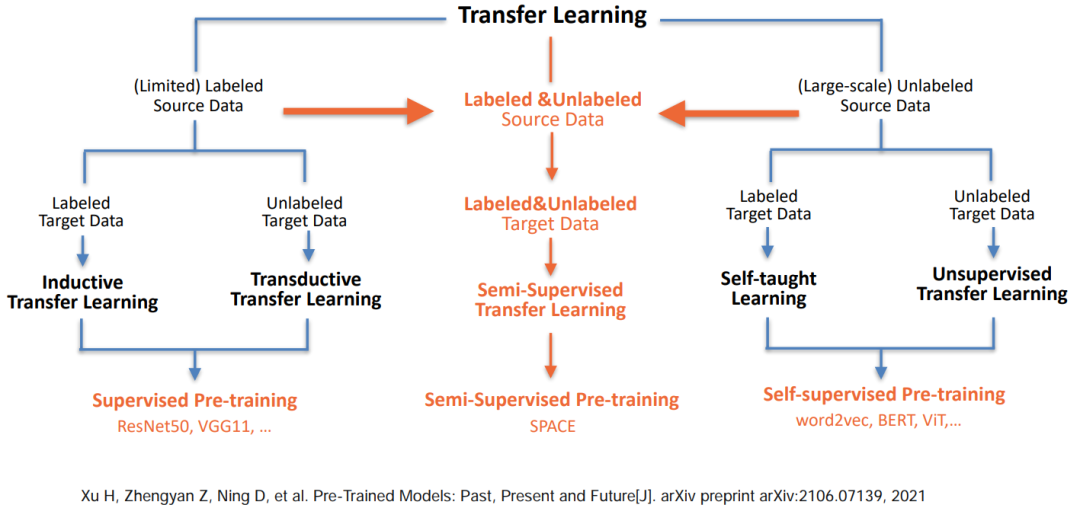
干货!半监督预训练对话模型 SPACE

Etcd build a highly available etcd cluster
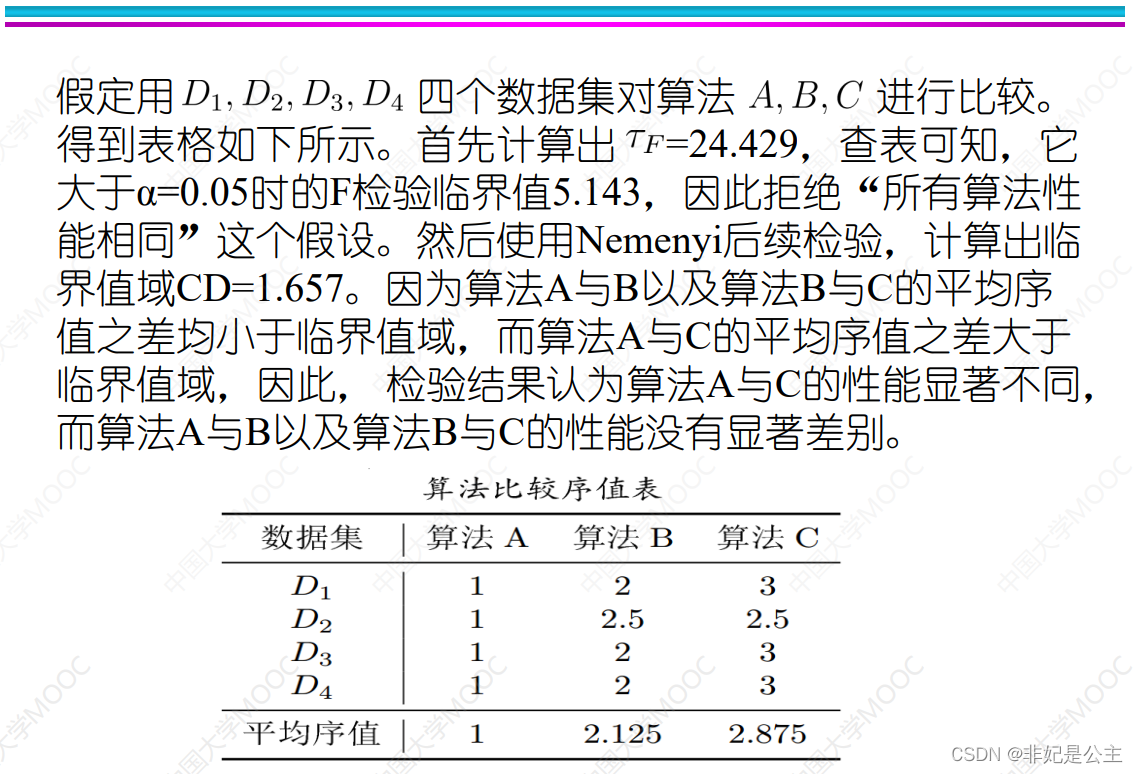
机器学习02:模型评估
随机推荐
一文了解MySQL事务隔离级别
What else do you not know about new map()
NPM installation
华为云云原生容器综合竞争力,中国第一!
C (WinForm) the current thread is not in a single threaded unit, so ActiveX controls cannot be instantiated
Deeply cultivate 5g, and smart core continues to promote 5g applications
Domain name resolution, reverse domain name resolution nbtstat
EasyX second lesson
云安全日报220705:红帽PHP解释器发现执行任意代码漏洞,需要尽快升级
Machine learning 01: Introduction
CMake教程Step1(基本起点)
Is it safe for qiniu business school to open a stock account? Is it reliable?
SQL删除重复数据的实例教程
菜刀,蚁剑,冰蝎,哥斯拉的流量特征
[first lecture on robot coordinate system]
Summary of optimization scheme for implementing delay queue based on redis
【性能测试】全链路压测
URP下Alpha从Gamma空间到Linner空间转换(二)——多Alpha贴图叠加
【testlink】TestLink1.9.18常见问题解决方法
Debug kernel code through proc interface