当前位置:网站首页>Machine learning compilation lesson 2: tensor program abstraction
Machine learning compilation lesson 2: tensor program abstraction
2022-07-05 16:58:00 【Self driving pupils】
02 Tensor program abstraction 【MLC- Machine learning compiles Chinese version 】
course home :https://mlc.ai/summer22-zh/
List of articles
In this chapter , We will discuss the abstraction of single unit computing steps and possible transformations of these abstractions in machine learning compilation .
2.1 Metatensor function
In the overview of the previous chapter , We introduce the process of machine learning compilation, which can be regarded as Transformation between tensor functions . The execution of a typical machine learning model includes many steps to convert the input tensors into the final prediction , Each of these steps is called Metatensor function (primitive tensor function).
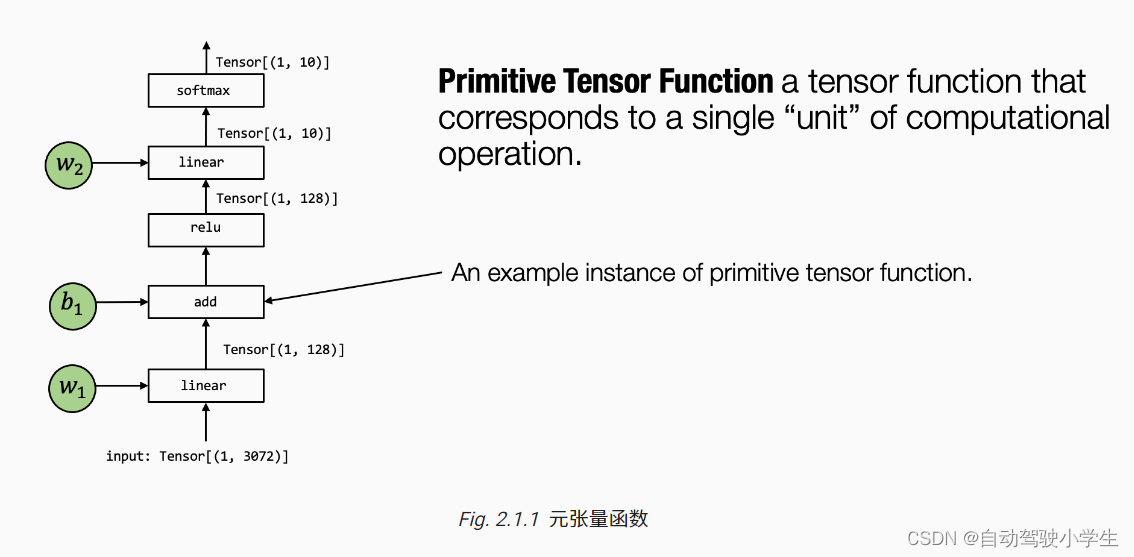
In the picture above , Tensor operator linear, add, relu and softmax Are all metatensor functions . In particular , Many different abstractions can represent ( And the implementation ) The same meta tensor function ( As shown in the figure below ). We can choose to call the precompiled Framework Library ( Such as torch.add and numpy.add) And take advantage of Python In the implementation of . In practice , Metatensor functions are, for example C or C++ Implemented in low-level languages , And sometimes it will include some assembly code .

Many machine learning frameworks provide the compilation process of machine learning models , To transform the meta tensor function into a more specialized 、 Functions for specific work and deployment environments .
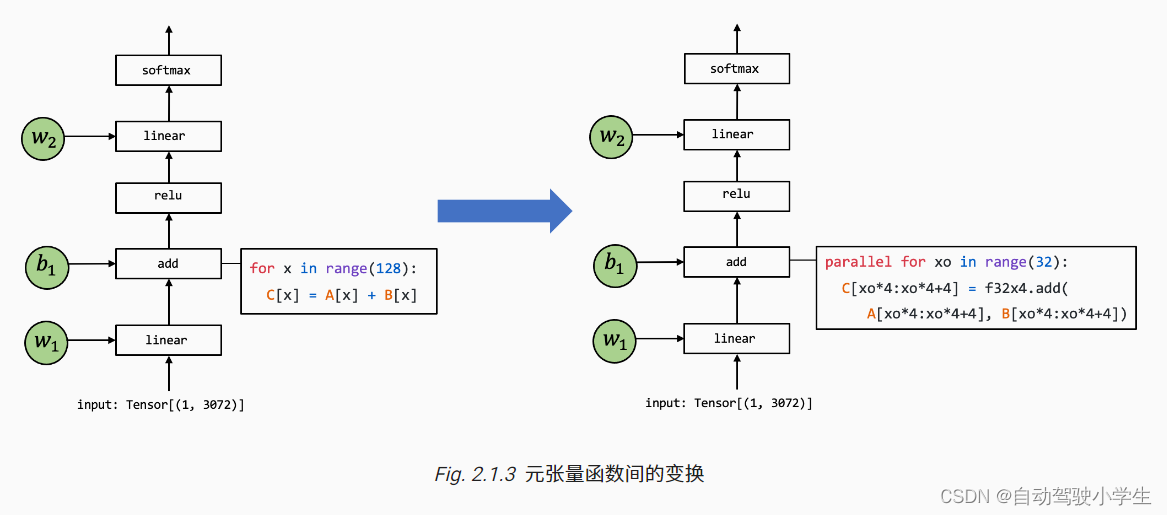
The above figure shows a meta tensor function add The implementation of is transformed to another example of a different implementation , The code on the right is a pseudocode that represents possible combinatorial optimization : The loop in the code on the left is split into a length of 4 Unit of ,f32x4.add The corresponding function is a special function that performs vector addition calculation .
2.2 Tensor program abstraction
In the previous section, we talked about the need for the transformation of tensor functions . In order that we can transform the meta tensor function more effectively , We need an effective abstraction to represent these functions .
Generally speaking , The abstraction of a typical meta tensor function implementation includes the following components : A multidimensional array that stores data , Loop nesting that drives tensor computation as well as The calculation part itself The sentence of .

We call this kind of abstraction Tensor program abstraction . An important property of tensor program abstraction is , They can be changed by a series of effective program transformations .
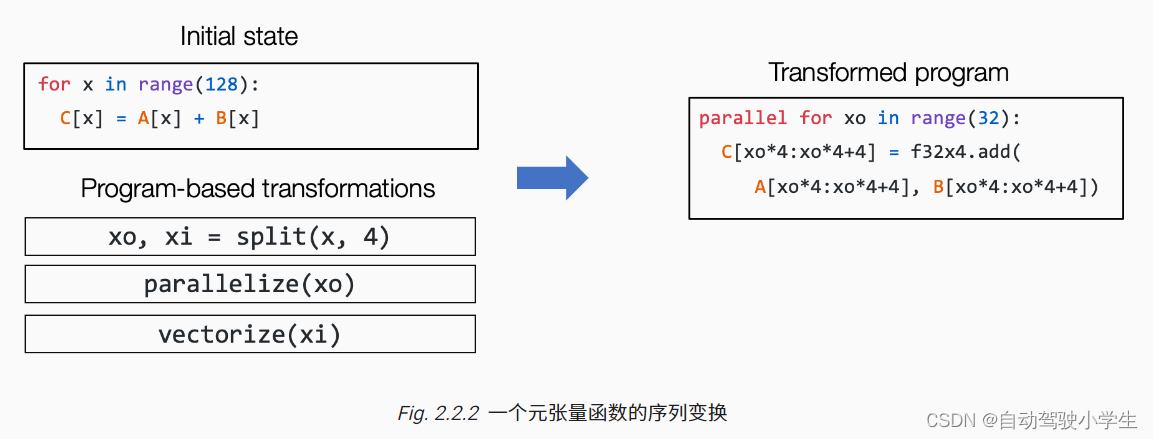
for example , We can operate through a set of transformations ( Such as circular split 、 Parallelism and vectorization ) Change an initial cycle program on the left side of the above figure to the program on the right .
2.2.1 Other structures in tensor program abstraction
It is important to , We cannot change the program arbitrarily , For example, this may be because some calculations depend on the order between loops . But fortunately , Most of the metatensor functions we are interested in have good properties ( For example, the independence between loop iterations ).
The tensor program can combine this additional information into a part of the program , To make program transformation more convenient .

for instance , The program in the above figure contains additional T.axis.spatial mark , indicate vi This particular variable is mapped to the loop variable i, And all iterations are independent . This information is not necessary to execute the program , But it will make it more convenient for us to change this program . In this case , We know that we can safely parallelize or reorder all and vi About the cycle , As long as the actual implementation vi Value of from 0 To 128 The order of change .
2.3 Tensor program transformation practice
2.3.1 Install the relevant package
For the purpose of this course , We will use TVM ( An open source machine learning compilation framework ) Some of them are under continuous development . We provide the following commands for MLC Install a packaged version of the course .
python3 -m pip install mlc-ai-nightly -f https://mlc.ai/wheels
2.3.2 Construct tensor program
Let's first construct a tensor program that performs two vector addition .
import numpy as np
import tvm
from tvm.ir.module import IRModule
from tvm.script import tir as T
@tvm.script.ir_module
class MyModule:
@T.prim_func
def main(A: T.Buffer[128, "float32"],
B: T.Buffer[128, "float32"],
C: T.Buffer[128, "float32"]):
# extra annotations for the function
T.func_attr({
"global_symbol": "main", "tir.noalias": True})
for i in range(128):
with T.block("C"):
# declare a data parallel iterator on spatial domain
vi = T.axis.spatial(128, i)
C[vi] = A[vi] + B[vi]
TVMScript It's a way for us to Python The way to represent tensor programs in the form of abstract syntax trees . Notice that this code does not actually correspond to a Python Program , Instead, it corresponds to a tensor program in the compilation process of machine learning .TVMScript The language of is designed to communicate with Python Corresponding to grammar , And in Python On the basis of grammar, additional structure is added to help program analysis and transformation .
type(MyModule)
tvm.ir.module.IRModule
MyModule yes IRModule An example of a data structure , Is a set of tensor functions .
We can go through script Function to get this IRModule Of TVMScript Express . This function is useful for checking between step-by-step program transformations IRModule Very helpful for .
print(MyModule.script())
@tvm.script.ir_module
class Module:
@tir.prim_func
def func(A: tir.Buffer[128, "float32"], B: tir.Buffer[128, "float32"], C: tir.Buffer[128, "float32"]) -> None:
# function attr dict
tir.func_attr({
"global_symbol": "main", "tir.noalias": True})
# body
# with tir.block("root")
for i in tir.serial(128):
with tir.block("C"):
vi = tir.axis.spatial(128, i)
tir.reads(A[vi], B[vi])
tir.writes(C[vi])
C[vi] = A[vi] + B[vi]
2.3.3 Compile and run
At any moment , We can all go through build Will a IRModule Into executable functions .
rt_mod = tvm.build(MyModule, target="llvm") # The module for CPU backends.
type(rt_mod)
tvm.driver.build_module.OperatorModule
After compilation ,mod Contains a set of executable functions . We can get the corresponding functions by their names .
func = rt_mod["main"]
func
<tvm.runtime.packed_func.PackedFunc at 0x7fd5ad30aa90>
a = tvm.nd.array(np.arange(128, dtype="float32"))
b = tvm.nd.array(np.ones(128, dtype="float32"))
c = tvm.nd.empty((128,), dtype="float32")
To execute this function , We are TVM runtime Create three NDArray, Then execute and call this function .
func(a, b, c)
print(a)
[ 0. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13.
14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27.
28. 29. 30. 31. 32. 33. 34. 35. 36. 37. 38. 39. 40. 41.
42. 43. 44. 45. 46. 47. 48. 49. 50. 51. 52. 53. 54. 55.
56. 57. 58. 59. 60. 61. 62. 63. 64. 65. 66. 67. 68. 69.
70. 71. 72. 73. 74. 75. 76. 77. 78. 79. 80. 81. 82. 83.
84. 85. 86. 87. 88. 89. 90. 91. 92. 93. 94. 95. 96. 97.
98. 99. 100. 101. 102. 103. 104. 105. 106. 107. 108. 109. 110. 111.
112. 113. 114. 115. 116. 117. 118. 119. 120. 121. 122. 123. 124. 125.
126. 127.]
print(b)
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1.]
print(c)
[ 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14.
15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28.
29. 30. 31. 32. 33. 34. 35. 36. 37. 38. 39. 40. 41. 42.
43. 44. 45. 46. 47. 48. 49. 50. 51. 52. 53. 54. 55. 56.
57. 58. 59. 60. 61. 62. 63. 64. 65. 66. 67. 68. 69. 70.
71. 72. 73. 74. 75. 76. 77. 78. 79. 80. 81. 82. 83. 84.
85. 86. 87. 88. 89. 90. 91. 92. 93. 94. 95. 96. 97. 98.
99. 100. 101. 102. 103. 104. 105. 106. 107. 108. 109. 110. 111. 112.
113. 114. 115. 116. 117. 118. 119. 120. 121. 122. 123. 124. 125. 126.
127. 128.]
2.3.4 Tensor program transformation
Now we begin to transform the tensor program . A tensor program can be implemented through an auxiliary called scheduling (schedule) The data structure is transformed .
sch = tvm.tir.Schedule(MyModule)
type(sch)
tvm.tir.schedule.schedule.Schedule
We first try to split the loop .
# Get block by its name
block_c = sch.get_block("C")
# Get loops surrounding the block
(i,) = sch.get_loops(block_c)
# Tile the loop nesting.
i_0, i_1, i_2 = sch.split(i, factors=[None, 4, 4])
print(sch.mod.script())
@tvm.script.ir_module
class Module:
@tir.prim_func
def func(A: tir.Buffer[128, "float32"], B: tir.Buffer[128, "float32"], C: tir.Buffer[128, "float32"]) -> None:
# function attr dict
tir.func_attr({
"global_symbol": "main", "tir.noalias": True})
# body
# with tir.block("root")
for i_0, i_1, i_2 in tir.grid(8, 4, 4):
with tir.block("C"):
vi = tir.axis.spatial(128, i_0 * 16 + i_1 * 4 + i_2)
tir.reads(A[vi], B[vi])
tir.writes(C[vi])
C[vi] = A[vi] + B[vi]
We can reorder these cycles . Now we will i_2 Move to i_1 On the outside .
sch.reorder(i_0, i_2, i_1)
print(sch.mod.script())
@tvm.script.ir_module
class Module:
@tir.prim_func
def func(A: tir.Buffer[128, "float32"], B: tir.Buffer[128, "float32"], C: tir.Buffer[128, "float32"]) -> None:
# function attr dict
tir.func_attr({
"global_symbol": "main", "tir.noalias": True})
# body
# with tir.block("root")
for i_0, i_2, i_1 in tir.grid(8, 4, 4):
with tir.block("C"):
vi = tir.axis.spatial(128, i_0 * 16 + i_1 * 4 + i_2)
tir.reads(A[vi], B[vi])
tir.writes(C[vi])
C[vi] = A[vi] + B[vi]
Last , We can label the outermost loop that we want to parallel .
sch.parallel(i_0)
print(sch.mod.script())
@tvm.script.ir_module
class Module:
@tir.prim_func
def func(A: tir.Buffer[128, "float32"], B: tir.Buffer[128, "float32"], C: tir.Buffer[128, "float32"]) -> None:
# function attr dict
tir.func_attr({
"global_symbol": "main", "tir.noalias": True})
# body
# with tir.block("root")
for i_0 in tir.parallel(8):
for i_2, i_1 in tir.grid(4, 4):
with tir.block("C"):
vi = tir.axis.spatial(128, i_0 * 16 + i_1 * 4 + i_2)
tir.reads(A[vi], B[vi])
tir.writes(C[vi])
C[vi] = A[vi] + B[vi]
We can compile and run the transformed program .
transformed_mod = tvm.build(sch.mod, target="llvm") # The module for CPU backends.
transformed_mod["main"](a, b, c)
print(c)
[ 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14.
15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28.
29. 30. 31. 32. 33. 34. 35. 36. 37. 38. 39. 40. 41. 42.
43. 44. 45. 46. 47. 48. 49. 50. 51. 52. 53. 54. 55. 56.
57. 58. 59. 60. 61. 62. 63. 64. 65. 66. 67. 68. 69. 70.
71. 72. 73. 74. 75. 76. 77. 78. 79. 80. 81. 82. 83. 84.
85. 86. 87. 88. 89. 90. 91. 92. 93. 94. 95. 96. 97. 98.
99. 100. 101. 102. 103. 104. 105. 106. 107. 108. 109. 110. 111. 112.
113. 114. 115. 116. 117. 118. 119. 120. 121. 122. 123. 124. 125. 126.
127. 128.]
2.3.5 Through tensor expression (Tensor Expression,TE) Construct tensor program
In the previous example , We use it directly TVMScript Construct tensor program . In practice, , It is very helpful to construct these functions conveniently through existing definitions . Tensor expression (tensor expression) It is a program that helps us transform some tensor calculations that can be expressed by expressions into tensor programs API.
# namespace for tensor expression utility
from tvm import te
# declare the computation using the expression API
A = te.placeholder((128, ), name="A")
B = te.placeholder((128, ), name="B")
C = te.compute((128,), lambda i: A[i] + B[i], name="C")
# create a function with the specified list of arguments.
func = te.create_prim_func([A, B, C])
# mark that the function name is main
func = func.with_attr("global_symbol", "main")
ir_mod_from_te = IRModule({
"main": func})
print(ir_mod_from_te.script())
@tvm.script.ir_module
class Module:
@tir.prim_func
def func(A: tir.Buffer[128, "float32"], B: tir.Buffer[128, "float32"], C: tir.Buffer[128, "float32"]) -> None:
# function attr dict
tir.func_attr({
"global_symbol": "main", "tir.noalias": True})
# body
# with tir.block("root")
for i0 in tir.serial(128):
with tir.block("C"):
i = tir.axis.spatial(128, i0)
tir.reads(A[i], B[i])
tir.writes(C[i])
C[i] = A[i] + B[i]
2.3.6 Transform a matrix multiplication program
In the example above , We show how to transform a vector addition program . Now let's try to apply some transformation to a slightly more complex program —— Matrix multiplication program . We first use tensor expressions API Construct the initial tensor program , Compile and execute it .
from tvm import te
M = 1024
K = 1024
N = 1024
# The default tensor type in tvm
dtype = "float32"
target = "llvm"
dev = tvm.device(target, 0)
# Algorithm
k = te.reduce_axis((0, K), "k")
A = te.placeholder((M, K), name="A")
B = te.placeholder((K, N), name="B")
C = te.compute((M, N), lambda m, n: te.sum(A[m, k] * B[k, n], axis=k), name="C")
# Default schedule
func = te.create_prim_func([A, B, C])
func = func.with_attr("global_symbol", "main")
ir_module = IRModule({
"main": func})
print(ir_module.script())
func = tvm.build(ir_module, target="llvm") # The module for CPU backends.
a = tvm.nd.array(np.random.rand(M, K).astype(dtype), dev)
b = tvm.nd.array(np.random.rand(K, N).astype(dtype), dev)
c = tvm.nd.array(np.zeros((M, N), dtype=dtype), dev)
func(a, b, c)
evaluator = func.time_evaluator(func.entry_name, dev, number=1)
print("Baseline: %f" % evaluator(a, b, c).mean)
@tvm.script.ir_module
class Module:
@tir.prim_func
def func(A: tir.Buffer[(1024, 1024), "float32"], B: tir.Buffer[(1024, 1024), "float32"], C: tir.Buffer[(1024, 1024), "float32"]) -> None:
# function attr dict
tir.func_attr({
"global_symbol": "main", "tir.noalias": True})
# body
# with tir.block("root")
for i0, i1, i2 in tir.grid(1024, 1024, 1024):
with tir.block("C"):
m, n, k = tir.axis.remap("SSR", [i0, i1, i2])
tir.reads(A[m, k], B[k, n])
tir.writes(C[m, n])
with tir.init():
C[m, n] = tir.float32(0)
C[m, n] = C[m, n] + A[m, k] * B[k, n]
Baseline: 2.967772
We can transform loops in tensor programs , Make the memory access mode more cache friendly under the new loop . Let's try the following scheduling .
sch = tvm.tir.Schedule(ir_module)
type(sch)
block_c = sch.get_block("C")
# Get loops surrounding the block
(y, x, k) = sch.get_loops(block_c)
block_size = 32
yo, yi = sch.split(y, [None, block_size])
xo, xi = sch.split(x, [None, block_size])
sch.reorder(yo, xo, k, yi, xi)
print(sch.mod.script())
func = tvm.build(sch.mod, target="llvm") # The module for CPU backends.
c = tvm.nd.array(np.zeros((M, N), dtype=dtype), dev)
func(a, b, c)
evaluator = func.time_evaluator(func.entry_name, dev, number=1)
print("after transformation: %f" % evaluator(a, b, c).mean)
@tvm.script.ir_module
class Module:
@tir.prim_func
def func(A: tir.Buffer[(1024, 1024), "float32"], B: tir.Buffer[(1024, 1024), "float32"], C: tir.Buffer[(1024, 1024), "float32"]) -> None:
# function attr dict
tir.func_attr({
"global_symbol": "main", "tir.noalias": True})
# body
# with tir.block("root")
for i0_0, i1_0, i2, i0_1, i1_1 in tir.grid(32, 32, 1024, 32, 32):
with tir.block("C"):
m = tir.axis.spatial(1024, i0_0 * 32 + i0_1)
n = tir.axis.spatial(1024, i1_0 * 32 + i1_1)
k = tir.axis.reduce(1024, i2)
tir.reads(A[m, k], B[k, n])
tir.writes(C[m, n])
with tir.init():
C[m, n] = tir.float32(0)
C[m, n] = C[m, n] + A[m, k] * B[k, n]
after transformation: 0.296419
Try to change batch_size Value , See what performance you can get . In practice , We will use an automated system to search in a possible transformation space to find the best program transformation .
2.4 summary
The meta tensor function represents the single unit computation in the computation of machine learning model . A machine learning compilation process can selectively transform the implementation of meta tensor functions .
A tensor program is an efficient abstraction of a tensor function . Key ingredients include :
Multidimensional arrays , A nested loop , Calculation statement. Program transformation can be used to speed up the execution of tensor programs . Additional structures in tensor programs can provide more information for program transformation .
边栏推荐
- 国产芯片产业链两条路齐头并进,ASML真慌了而大举加大合作力度
- Combined use of vant popup+ other components and pit avoidance Guide
- 微信公众号网页授权登录实现起来如此简单
- Application of threshold homomorphic encryption in privacy Computing: Interpretation
- 数据访问 - EntityFramework集成
- [Jianzhi offer] 61 Shunzi in playing cards
- [729. My schedule I]
- Keras crash Guide
- Benji Bananas 会员通行证持有人第二季奖励活动更新一览
- Jarvis OJ Telnet Protocol
猜你喜欢
Learnopongl notes (I)
Win11 prompt: what if the software cannot be downloaded safely? Win11 cannot download software safely
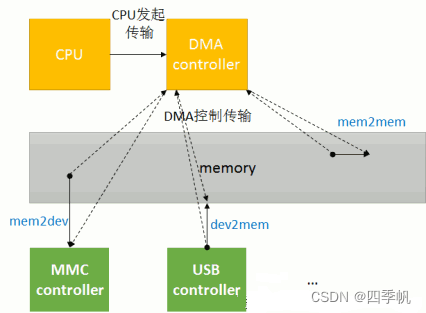
Copy mode DMA
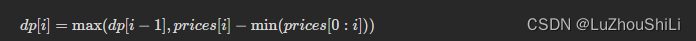
【剑指 Offer】63. 股票的最大利润

【刷題篇】鹅廠文化衫問題
Detailed explanation of use scenarios and functions of polar coordinate sector diagram

Scratch colorful candied haws Electronic Society graphical programming scratch grade examination level 3 true questions and answers analysis June 2022

美国芯片傲不起来了,中国芯片成功在新兴领域夺得第一名

ECU introduction

China Radio and television officially launched 5g services, and China Mobile quickly launched free services to retain users
随机推荐
二叉树相关OJ题
DenseNet
Hiengine: comparable to the local cloud native memory database engine
[brush title] goose factory shirt problem
Domestic API management artifact used by the company
How to install MySQL
Jarvis OJ Webshell分析
If you can't afford a real cat, you can use code to suck cats -unity particles to draw cats
Solve cmakelist find_ Package cannot find Qt5, ECM cannot be found
[wechat applet] read the life cycle and route jump of the applet
[Jianzhi offer] 66 Build product array
【729. 我的日程安排錶 I】
C how TCP restricts the access traffic of a single client
麻烦问下,DMS中使用Redis语法是以云数据库Redis社区版的命令为参考的嘛
Get ready for the pre-season card game MotoGP ignition champions!
Apple has abandoned navigationview and used navigationstack and navigationsplitview to implement swiftui navigation
[61dctf]fm
[echart] resize lodash to realize chart adaptation when window is zoomed
齐宣王典故
C# TCP如何限制单个客户端的访问流量