当前位置:网站首页>golang刷leetcode动态规划(11)不同路径
golang刷leetcode动态规划(11)不同路径
2022-08-02 18:54:00 【用户9710217】
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。
问总共有多少条不同的路径?
例如,上图是一个7 x 3 的网格。有多少可能的路径?
说明:m 和 n 的值均不超过 100。
示例 1:
输入: m = 3, n = 2
输出: 3
解释:
从左上角开始,总共有 3 条路径可以到达右下角。
1. 向右 -> 向右 -> 向下
2. 向右 -> 向下 -> 向右
3. 向下 -> 向右 -> 向右
示例 2:
输入: m = 7, n = 3
输出: 28
解题思路:
1,这个问题可以拆解成子问题,并且可以用子问题的结果来求最终结果,典型的动态规划
2,step[i,j]路径数=step[i,j-1] +step[i-1,j]
3,用到了i-1,j-1;所以用递增的方式
代码
func uniquePaths(m int, n int) int {
step:=make([][]int,m)
for i:=0;i<m;i++{
step[i]=make([]int,n)
step[i][0]=1
}
for i:=0;i<n;i++{
step[0][i]=1
}
for i:=1;i<m;i++{
for j:=1;j<n;j++{
step[i][j]=step[i-1][j]+step[i][j-1]
}
}
return step [m-1][n-1]
}边栏推荐
猜你喜欢
Mppt光伏最大功率点跟踪控制matlab仿真

我靠这套笔记自学,拿下字节50万offer....
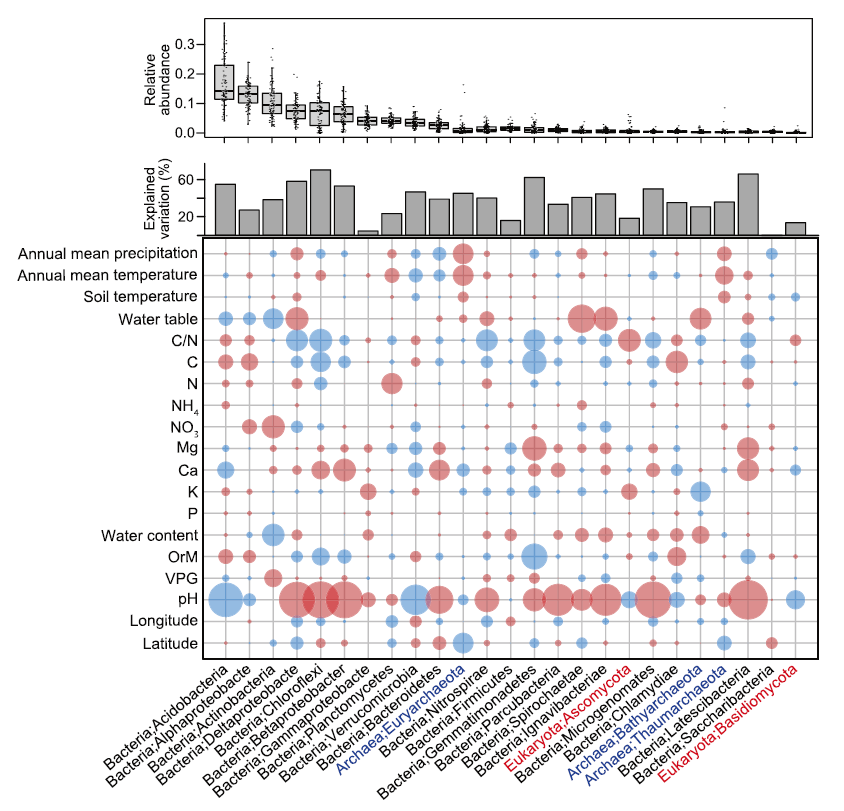
NC | 土壤微生物组的结构和功能揭示全球湿地N2O释放

Therapy | How to Identify and Deal with Negative Thoughts
动态折线图,制作原来是这么简单
安装Mac版Mysql卡在Installation阶段,彻底清理mysql并重装mysql
T31开发笔记:metaipc测试

【LeetCode】118. 杨辉三角 - Go 语言题解

什么是现场服务管理系统(FSM)?有什么好处?
Golang swagger :missing required param comment parameters
随机推荐
Mppt photovoltaic maximum power point tracking control matlab simulation
ssh配置
药品研发--工艺技术人员积分和职务考核评估管理办法
Mobile Banking Experience Test: How to Get the Real User Experience
golang刷leetcode 数学(1) 丑数系列
洛谷P1502 窗口的星星
arcgis 分子式标注
日常开发中,String类中常用的方法
松鼠短视频系统为用户加入随机头像代码-快速为用户加上随机头衔
如何获取EasyCVR平台设备通道的RTMP视频流地址?
7.23 - 每日一题 - 408
Based on OpenGL glaciers and firebird (illumination calculation model, visual, particle system)
Why young people are snapping up domestic iPhone, because it is much cheaper and more populist
请教下,1.0.0和1.0.2的底层数据库表结构有变化吗?
7.21 - 每日一题 - 408
【动态规划专项训练】基础篇
想通过FC连接RDS mysql。是不是将FC服务角色添加rds权限后,就可以通过地址,端口建连了呢
1.0.0到1.0.2的底层数据库表的更新,需要再重新自建数据库吗?
spack install reports an error /tmp/ccBDQNaB.s: Assembler message:
golang面试题