当前位置:网站首页>[ta - Frost Wolf May - 100 people plan] 2.3 Introduction aux fonctions communes
[ta - Frost Wolf May - 100 people plan] 2.3 Introduction aux fonctions communes
2022-07-01 03:42:00 【Zczplus】
【TA-Frost Wolf_may-《Le programme 100 personnes》】2.3 Introduction aux fonctions communes
- 2.3HLSLFonctions communes
【TA-Frost Wolf_may-《Le programme 100 personnes》】2.3 Introduction aux fonctions communes
- 2.3HLSLFonctions communes
2.3HLSLFonctions communes
2.3.1 Opérations mathématiques de base
max(a,b) min(a,b) mul(a,b) abs(a) round(x)
sqrt(x) RetourxRacine carrée de
rsqrt(x) RetourxInverse de la racine carrée de
degrees(x) Convertir les radians en angles
redians(x) Convertir l'angle en radians
noise(x) Fonction de bruit
2.3.2 Fonction de paire de puissance
pow(x,y) xDeyPuissance secondaire(xEty Peut être une variable indépendante ou un nombre spécifique )
exp(x) Retour àeFonction exponentielle de base
exp2(value x) Retour à2En bas.,x Est la puissance de l'exposant
ldexp(x,exp) RetourxAvec2Deexp Produit de la puissance
log(x)
log10(x)
log2(x)
frexp(x,out exp) Mettez le flotteur x Décomposé en taillis et exposants x = ret*2^exp, La valeur de retour est la queue ,exp La valeur retournée par le paramètre est exponentielle
(SixLe paramètre est0, La queue et l'exposant de cette fonction renvoient 0)
2.3.3 Fonctions trigonométriques et hyperboliques
sin(x) cos(x) tan(x)
sincos(x, out s, out c) Retourx Sinus et cosinus de
tan(y,x) asin(x) acos(x) atan(x) atan2(y,x) Retoury/xTangente à l'Arc de
Ce qui précèdex Les valeurs sont exprimées en radians
sinh(x) RetourxSinus hyperbolique de C'est - à - dire: (ex-e-x) / 2
cosh(x) RetourxCosinus hyperbolique de C'est - à - dire: (ex+e-x) / 2
tanh(x) RetourxSinus hyperbolique de C'est - à - dire: (ex-e-x) / (ex+e-x)
2.3.4 Classe de plage de données
ceil(x) Retour>=xLe plus petit entier de
floor(x) Retour<=xEntier maximum de
step(x,y) x<=yPour1,Sinon0
saturate(x) Le retourxClamp to0Et1Entre les valeurs
clamp(x,min,max) Prends ça.xLimité à[min,max]Dans le champ d'application,C'est - à - dire le jugementx Est - ce dans cet intervalle , Si oui, renvoie la valeur originale , Sinon, retourner la limite supérieure ou inférieure
fmod(x,y) RetourxC'est exact.yPrenez le reste
frac(x) RetourxLa partie décimale de
modf(x, out ip) Valeurx Divisé en parties décimales et entières ( Les symboles des Parties sont liés à xMême chose.)
ipRenvoie une partie entière, Renvoie la partie décimale de l'ensemble
Fonction d'interpolation
lerp(x,y,s) SelonsInxÀyInterpolation entre,Retourx*(1-s)+y*s;
smoothstep(min,max,x) SixIn[min, max]Dans le champ d'application, Renvoie entre 0Avec1 Lisse entre HermiteInterpolation,Utilisersmoothstep Créer une passe lisse entre deux valeurs . Par exemple, vous pouvez mélanger deux couleurs en douceur .
2.3.5 Classe de jugement de type
all(x) Déterminer si tous les composants de la quantité spécifiée sont non nuls , Renvoie si les deux ne sont pas nuls True,Sinonfalse(Scalaire、 Un vecteur ou une matrice peut )
clip(x) Si la valeur saisie est inférieure à zéro , Le Pixel courant est éliminé Souvent utilisé pour déterminer la portée (Pas seulement pour0,La valeur de retour estvoid),Ou testalpha, Si chaque composant représente la distance par rapport au plan , Peut également être utilisé pour simuler le plan de cisaillement
sign(x) Retourx Positif et négatif Six Moins de zéro renvoie -1,Six égal à zéro renvoie 0,Six Plus de zéro renvoie 1
isinf(x) Déterminer si c'est infini ou infinitésimal
isfinite(x) Jugementx Les paramètres sont - ils limités
isnan(x) Déterminer si oui ou nonNAN
2.3.6 Classe vectorielle et matricielle
length(v)
normalize(v)
distance(a,b) Représentation:Deux vecteurs, Renvoie la somme des carrés de la différence de chaque composant sous le numéro racine (Non, c'est vrai. La distance de la fin )
dot(a,b) Produit dot
cross(a,b) Produit croisé
determinant(m) Retour à la matricem Valeur calculée comme déterminant
transpose(m) Retour à la matricemMatrice de transposition pour
2.3.7 Classe de calcul de la lumière
reflect(i,n) Retour àiPour la direction incidente,n Lumière réfléchie dans la direction normale
refract(i,n,ri) Retour àiPour le vecteur incident,n Pour la direction normale ,ri La lumière réfractée pour l'indice de réfraction
lit(n_dot_I, n_dot_h, m) Correspondant séparément(normallight,normalVecteur demi - angulaireh,Coefficient de réflexion spéculairem) Renvoie un vecteur d'éclairage (Éclairage ambiant,Lumière diffuse, Spéculaire spéculaire ,1)
faceforward(n,i,ng) On obtient que l'entrée et la sortie du vecteur normal de surface orienté vers la vue sont des vecteurs homogènes ,Retour-n*sign(dot(i,ng))(normal,light,normal)
Vecteur d'éclairage
Vecteur d'éclairage(Éclairage ambiant,Lumière diffuse, Spéculaire spéculaire ,1)(BlinnModèle)
2.3.8 Recherche de texture
GPU Dans le traitement des éléments (PixelShader) L'étape est dans l'espace de l'écran XY Chaque pixel dans le système de coordonnées correspond à la texture pour trouver le pixel correspondant pour déterminer la couleur du Pixel ( Les noms sont compréhensibles )
1D
Les méthodes sont moins fréquentes , ..Peu de données sont stockées de cette façon , Tableau correspondant à une dimension
2D
Tableau correspondant à 2D ,C'est la matrice
3DRecherche de texture
Recherche de données 3D , Composé d'un tableau bidimensionnel à plusieurs niveaux .
tex(s,t) Dans un échantillonneur de texture donné (s, Se réfère à l'image échantillonnée )Dans le cas de,Adoptiont(1D Sous le scalaire ,2D、3DVecteur, C'est - à - dire les coordonnées de position ) Pour déterminer les données d'empreinte .
La texture projetée est pertinente(Ce n'est pas très clair Regarde encore.)
tex1Dproj(s, t) Projeter la texture comme une diapositive dans la scène , Les coordonnées de la texture projetée sont d'abord calculées à l'aide de la technique de texture projetée ( En raison du changement d'angle entre la lumière projetée et la surface projetée , Donc les coordonnées de la texture projetée ne sont pas une simple échelle , D'autres problèmes comme le biseautage peuvent survenir , En outre, l'irrégularité de la surface projetée est également un problème à résoudre ), Enfin, utilisez les coordonnées de texture projetées pour la recherche de pixels .
ddx、ddyConcentrez - vous sur vos recherches
mipmap
Bonne photo. , Mieux utilisé pour comprendre pourquoi la mémoire n'est utilisée que 1/3
Recherche de textures stéréo
Contrairement à la recherche 3D , Des faces spécifiques doivent être spécifiées , Et plus de performance .
Résumé
Écrivez ce que vous trouvez le plus commun5Fonctions?
- Découvrez plus d'opérations sur les matrices et les vecteurs en regardant l'essentiel de l'introduction ,Parmi eux mul(x,y) Absolument indispensable comme point d'application à haute fréquence ;
- Les opérations normalisées devraient également être plus courantes ,Alors...saturate(x) Ça devrait être plus courant ;
- Fonction d'interpolation;
- La classe de calcul de la lumière devrait être l'emphase et la difficulté , En général, les objets sont éclairés , Ça devrait être une fonction courante ;
- Recherche de texture mipmap La fonction de corrélation est un problème inévitable tout au long du rendu , Donc C'est une fonction courante ;
ddx、ddyEtMipmap
RegardeGames101 P9, Je commence à comprendre .
- InMipmapMoyenne,ddxEtddy L'objectif principal de la méthode est de calculer la longueur de couverture des pixels d'écran dans les pixels d'image ,Par
L = MAX(sqrt(ddx(u, v)2, ddy(u, v)2)) On peut obtenir des longueurs approximatives des bords des rectangles recouverts de pixels ; - RéutilisationD=Log2(L) Obtenir ce qu'il faut MipmapNombre de couches,Prends - le.Log2(L)Parce que,Mipmap Chaque couche de 1/2,Trouve - le.Log2(L)Couche, En ce momentL Sur cette couche est la longueur unitaire , Cela permet d'économiser le processus de ré - échantillonnage ;
- Et,Log2(L) Non entier en général , Utilisez les deux Mipmap La couche est interpolée linéairement à nouveau , Peut rendre les résultats plus précis ,Donc,Mipmap La méthode est également appelée interpolation linéaire cubique .
边栏推荐
- Unexpected token o in JSON at position 1 ,JSON解析问题
- The method to measure the similarity of two vectors: cosine similarity, pytorch calculate cosine similarity: torch nn. CosineSimilarity(dim=1, eps=1e-08)
- Sort linked list (merge sort)
- Implement pow (x, n) function
- [small sample segmentation] interpretation of the paper: prior guided feature enrichment network for fee shot segmentation
- 6. Z 字形变换
- Review column - message queue
- AfxMessageBox和MessageBox的用法
- Complete knapsack problem
- 4、【WebGIS实战】软件操作篇——数据导入及处理
猜你喜欢

Random seed torch in deep learning manual_ seed(number)、torch. cuda. manual_ seed(number)
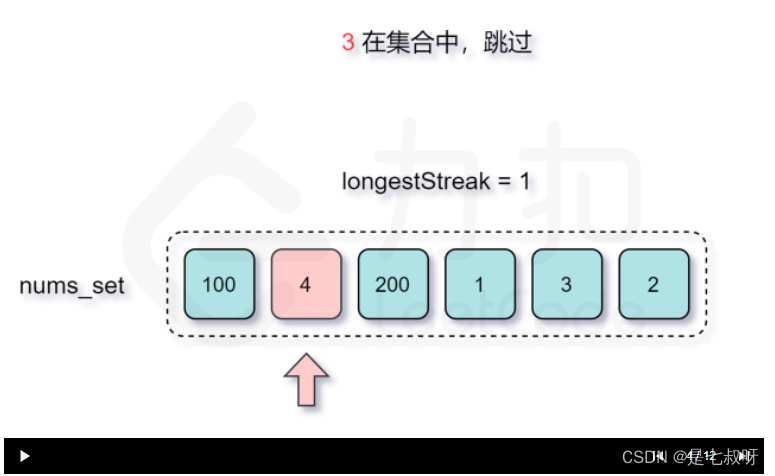
LeetCode 128最长连续序列(哈希set)

How to achieve 0 error (s) and 0 warning (s) in keil5

Bilinear upsampling and f.upsample in pytorch_ bilinear

数据库中COMMENT关键字的使用

Home online shopping project

Cookie&Session

Leetcode 31 next spread, leetcode 64 minimum path sum, leetcode 62 different paths, leetcode 78 subset, leetcode 33 search rotation sort array (modify dichotomy)

Are you still wasting brain cells for self-study? This interview note is definitely the ceiling of station C

【TA-霜狼_may-《百人计划》】2.4 传统经验光照模型
随机推荐
【伸手党福利】开发人员重装系统顺序
Gorilla/mux framework (RK boot): RPC error code design
Leetcode: offer 59 - I. maximum value of sliding window
Valentine's Day is nothing.
How to achieve 0 error (s) and 0 warning (s) in keil5
AfxMessageBox和MessageBox的用法
205. 同构字符串
idea插件备份表
二叉树神级遍历:Morris遍历
[party benefits] jsonobject to string, leave blank
214. 最短回文串
服务器渲染技术jsp
GCC usage, makefile summary
Blueprism registration, download and install -rpa Chapter 1
文件上传下载
How to use hybrid format to output ISO files? isohybrid:command not found
快速筛选打卡时间日期等数据:EXCEL筛选查找某一时间点是否在某一时间段内
TEC: Knowledge Graph Embedding with Triple Context
Feature pyramid networks for object detection
[nine day training] content III of the problem solution of leetcode question brushing Report