当前位置:网站首页>牛客题目——滑动窗口的最大值、矩阵最长递增路径、顺时针旋转矩阵、接雨水问题
牛客题目——滑动窗口的最大值、矩阵最长递增路径、顺时针旋转矩阵、接雨水问题
2022-08-02 19:21:00 【zhangzhang_one】
题目1——滑动窗口的最大值
给定一个长度为n的数组nums和滑动窗口的大小size,找出滑动窗口里数值的最大值。
例如输入数组{2,3,4,2,6,2,5,1}及滑动窗口的大小3,那么一共存在6个滑动窗口,他们的最大值分别为{4,4,6,6,6,5}。
要求:空间复杂度O(n),时间复杂度O(n)。
示例
输入:[2,3,4,2,6,2,5,1],3
输出:[4,4,6,6,6,5]
解题思路
暴力解决,直接遍历所有窗口,求出每个窗口的最大值。
但是时间复杂度较高O(nm),n为数组长度,m为窗口长度,空间复杂度O(1),返回结果不算入空间开销。
如果一个新的数字进入窗口,若它比窗口内其它数字都要大,那么这个数字之前的数字都不会选择,因为它们会比这个数字早离开窗口,在这期间的滑动窗口内,我们选择的都是这个最大的数字。
从这里分析可知,每次进入大数字时,应该排除掉之前的小值,并且每次窗口滑动时,需要弹出窗口最前面的值,所以可以选择双端队列来实现。
Java中双端队列的实现是ArrayDeque,它允许我们从两端进行存取操作,既可以作为栈,又可以作为队列使用。ArrayDeque类的方法如下:
- 头部插入元素:offerFirst(e),返回状态值;addFirst(e),失败会抛出异常;
- 头部移除元素:pollFirst(),删除并返回元素;removeFirst(),删除并返回元素,失败会抛出异常;
- 获取头部元素:peekFirst(),获取第一个元素;getFirst(),获取第一个元素,失败会抛出异常;
- 尾部插入元素: offerLast(e),返回状态值;addLast(e),失败会抛出异常;
- 尾部移除元素:pollLast(),删除并返回元素;removeLast(),删除并返回元素,失败会抛出异常;
- 获取尾部元素:peekLast(),获取最后一个元素;getLast(),获取最后一个元素,失败会抛出异常。
代码实现
//暴力解决
import java.util.*;
public class Solution {
public ArrayList<Integer> maxInWindows(int [] num, int size) {
ArrayList<Integer> res = new ArrayList<Integer>();
if(num.length < size){
return res;
}
//窗口数量为num.lenght-size+1
for(int i=0;i<num.length-size+1;i++){
int max = 0;
for(int j=i;j<i+size;j++){
if(num[j]>max)
max = num[j];
}
res.add(max);
}
return res;
}
}
//双端队列,时间复杂度O(n),空间复杂度为O(m),m为窗口的长度
import java.util.*;
public class Solution {
public ArrayList<Integer> maxInWindows(int [] num, int size) {
ArrayList<Integer> res = new ArrayList<Integer>();
if(num.length < size){
return res;
}
ArrayDeque<Integer> dq = new ArrayDeque<Integer>();
//先遍历一个窗口,
for(int i=0;i<size;i++){
//去掉前面的小于自己的值
while(!dq.isEmpty() && num[dq.peekLast()]<num[i])
dq.pollLast();
dq.add(i);
}
//遍历后续的数组
for(int i=size;i<num.length;i++){
res.add(num[dq.peekFirst()]);
//滑动窗口,移除队首的值
while(!dq.isEmpty() && dq.peekFirst()<(i-size+1))
dq.pollFirst();
//加入新的值前,去除掉比自己先进队列并小于自己的值
while(!dq.isEmpty() && num[dq.peekLast()]<num[i])
dq.pollLast();
dq.add(i);
}
res.add(num[dq.pollFirst()]);
return res;
}
}
题目2——矩阵最长递增路径
给定一个n行m列矩阵matrix,矩阵内所有数均为非负整数,你需要在矩阵中找到一条最长路径,使这条路径上的元素是递增的,并输出这条最长路径的长度。
这个路径必须满足以下条件:
- 对于每个单元格,你可以往上,下,左,右四个方向移动,不能在对角线方向上移动或移动到边界外。
- 不能走重复的单元格,即每个格子最多只能走一次。
要求:空间复杂度O(nm),时间复杂度O(nm)。
示例
输入:[[1,2,3],[4,5,6],[7,8,9]]
输出:5(最长路径1->2->3->6->9)
解题思路
使用深度优先搜索,从初始点开始,沿着同一个分支遍历,直到该分支结束,然后回溯到上一级继续沿着一个分支走到底,如此往复,直到所有结点都被访问到。
为了找到最长的递增路径,矩阵中的每个元素很有可能都是这个路径的起点,所以我们遍历整个矩阵中的元素,将每个元素作为起始点,然后进行深度优先搜索,寻找最长递增路径。具体做法如下:
- 使用一个数据b来记录每个起始点的最大递增路径,在递归过程中如果访问到了就不需要重复访问;
- 对于每个起始点,使用dfs查找最长的递增路径,dfs中,只要下一个位置比当前位置数字大,就可以深入。
代码实现
import java.util.*;
public class Solution {
public int dfs(int[][] matrix,int[][] b,int i,int j){
int n = matrix.length;
int m = matrix[0].length;
if(b[i][j] != 0)
return b[i][j];
b[i][j]++;
if(i-1>=0 && matrix[i-1][j]>matrix[i][j]){
b[i][j] = Math.max(b[i][j],dfs(matrix,b,i-1,j)+1);
}
if(i+1<n && matrix[i+1][j]>matrix[i][j]){
b[i][j] = Math.max(b[i][j],dfs(matrix,b,i+1,j)+1);
}
if(j-1>=0 && matrix[i][j-1]>matrix[i][j]){
b[i][j] = Math.max(b[i][j],dfs(matrix,b,i,j-1)+1);
}
if(j+1<m && matrix[i][j+1]>matrix[i][j]){
b[i][j] = Math.max(b[i][j],dfs(matrix,b,i,j+1)+1);
}
return b[i][j];
}
public int solve (int[][] matrix) {
int n = matrix.length;
int m = matrix[0].length;
int[][] b = new int[n][m];
int res = 0 ;
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
res = Math.max(res,dfs(matrix,b,i,j));
}
}
return res;
}
}
题目3——顺时针旋转矩阵
有一个n*n整数矩阵,请编写一个算法,将矩阵顺时针旋转90度,返回旋转后的矩阵。
要求:空间复杂度 O(n^2),时间复杂度 O(n^2)。
进阶:空间复杂度 O(1),时间复杂度 O(n^2)。
示例
输入:[[1,2,3],[4,5,6],[7,8,9]],3
输出:[[7,4,1],[8,5,2],[9,6,3]]
解题思路
使用一个辅助数组来存储新的矩阵,可以发现,原矩阵元素mat[i][j]旋转后该值在新矩阵的res[j][n-i-1]的位置,但是这样时间复杂度O(n^2),空间复杂度O(n ^2)。
可以发现顺时针旋转后的矩阵,就是矩阵转置,然后每行再翻转,这样只需要一个辅助变量即可实现旋转。
代码实现
import java.util.*;
public class Solution {
public int[][] rotateMatrix(int[][] mat, int n) {
int temp;
for(int i=0;i<n;i++){
for(int j=0;j<i;j++){
temp = mat[i][j];
mat[i][j] = mat[j][i];
mat[j][i] = temp;
}
}
for(int i=0;i<n;i++){
for(int j=0;j<n/2;j++){
temp = mat[i][j];
mat[i][j] = mat[i][n-j-1];
mat[i][n-j-1] = temp;
}
}
return mat;
}
}
题目4——接雨水问题
给定过一个整型数组arr,已知其中所有的值都是非负的,将这个数组看作一个柱子高度图,计算按此排列的柱子,下雨之后能接多少雨水(数组以外的区域高度视为0)。
要求:时间复杂度O(n)。
示例
输入:[3,1,2,5,2,4]
输出:5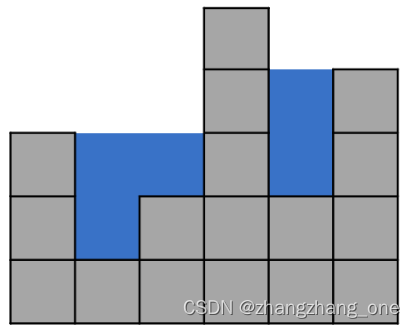
解题思路
我们可以将整个图看成一个水桶,两边是水桶的板,由较短的板控制水桶的最高水量,但是水桶中间可能会出现更高的边,这样就将一个水桶分割成了两个水桶,中间那条边就是两个水桶的边。
这样我们可以使用对撞指针往中间靠,如果遇到更低的柱子,就用较短的板减去这个底,就是这一列的接水量,如果遇到更高的柱子,就是新的边界,更新边界的大小。
代码实现
import java.util.*;
public class Solution {
public long maxWater (int[] arr) {
if(arr.length == 0)
return 0;
long res = 0;
int left = 0;
int right = arr.length-1;
int maxL = 0;
int maxR = 0;
//对撞指针往中间靠
while(left<right){
//每次维护往中间走的边界
maxL = Math.max(maxL,arr[left]);
maxR = Math.max(maxR,arr[right]);
if(maxR > maxL)
//短的边界减去底,就是这一列的接水量
res += maxL-arr[left++];
else
res += maxR-arr[right--];
}
return res;
}
}
边栏推荐
猜你喜欢
openlayers version update difference
2022-07-26
Golang swagger :missing required param comment parameters

译出我精彩 | 7月墨力翻译计划获奖名单公布
LSB利器-zsteg
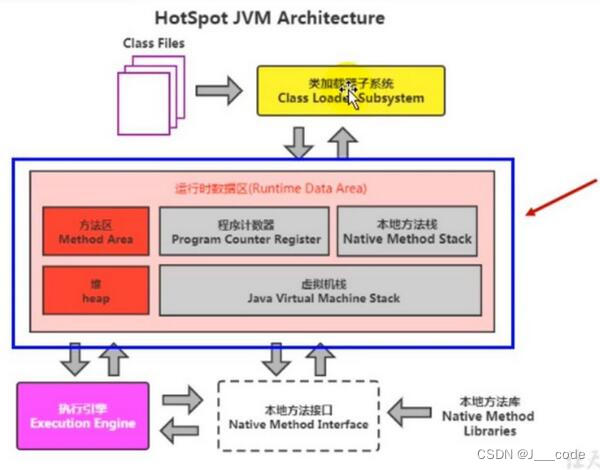
JVM内存和垃圾回收-03.运行时数据区概述及线程
Based on OpenGL glaciers and firebird (illumination calculation model, visual, particle system)
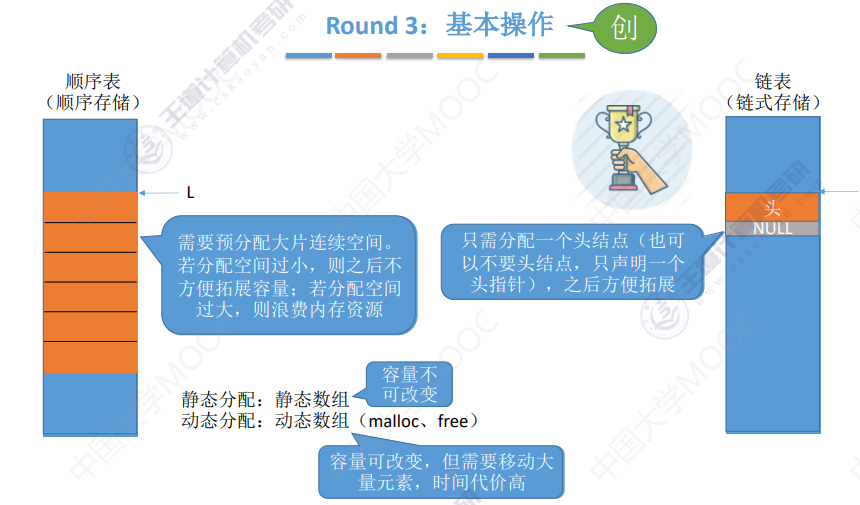
线性表(顺序表和链表)
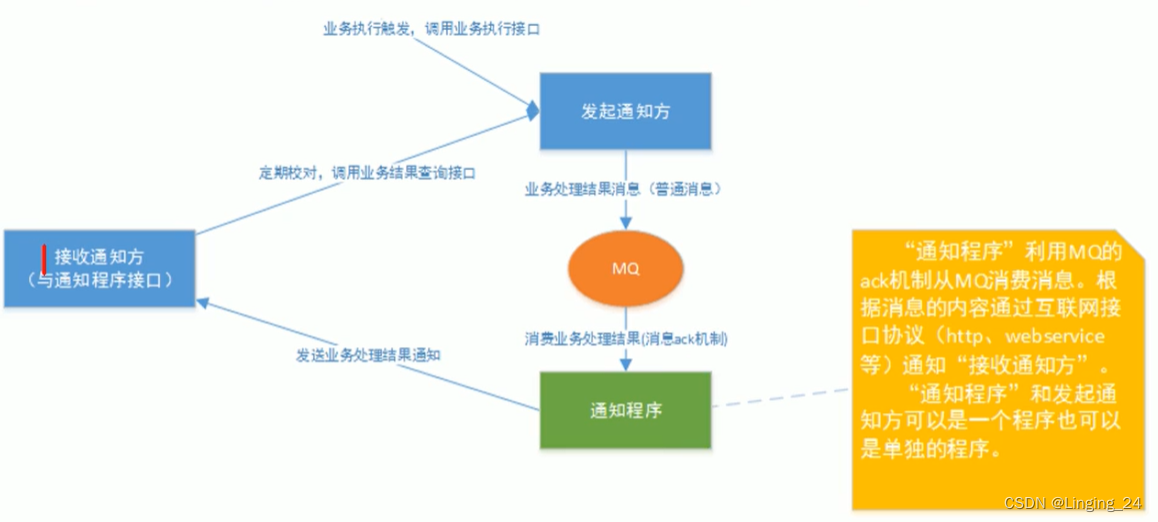
分布式事务
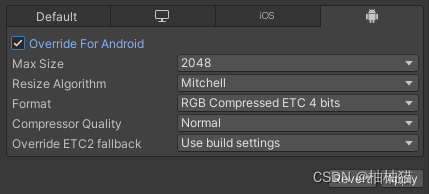
Unity 打包和切换平台|Build Settings窗口介绍
随机推荐
Geoserver+mysql+openlayers
golang刷leetcode 数学(1) 丑数系列
一些不错的博主
松鼠短视频系统为用户加入随机头像代码-快速为用户加上随机头衔
Unity 打包和切换平台|Build Settings窗口介绍
Go----Go 语言快速体验之开发环境搭建及第一个项目HelloWord
MySQL安装(详细,适合小白)
流量分析三—远程登陆
让你的应用完美适配平板
VMware虚拟机无法上网
SCANIA SCANIA OTL tag is introduced
ALV概念讲解
MYSQL关键字执行顺序?
[安洵杯 2019]easy_web
2022-07-26
线程池原理与实践|从入门到放弃,深度解析
Based on OpenGL glaciers and firebird (illumination calculation model, visual, particle system)
Gradle系列——Gradle的build.gradle文件详情,项目发布(基于Gradle文档7.5)day3-3
Mysql基础篇(视图)
Geoserver+mysql+openlayers2