动态规划常见实例详解

活动地址：CSDN21天学习挑战赛

什么是动态规划

首先很多人问，何为动态规划？动态规划（Dynamic Programming，DP）是运筹学的一个分支，是求解决策过程最优化的过程。通俗一点动态规划就是从下往上(从前向后)阶梯型求解数值。

那么动态规划和递归有什么区别和联系？

总的来说动态规划从前向后，递归从后向前，两者策略不同，并且一般动态规划效率高于递归。

不过都要考虑初始状态，上下层数据之间的联系。很多时候用动态规划能解决的问题，用递归也能解决不过很多时候效率不高可能会用到记忆化搜索。

不太明白?

就拿求解斐波那契额数列来说，如果直接用递归不优化，那么复杂度太多会进行很多重复的计算。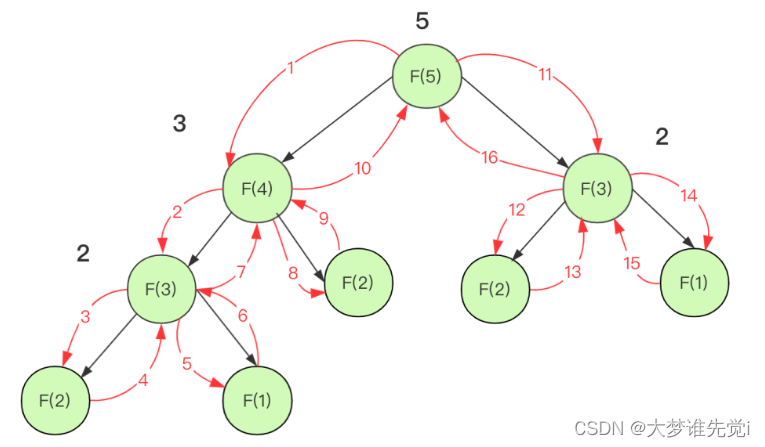

但是利用记忆化你可以理解为一层缓存，将求过的值存下来下次再遇到就直接使用就可以了。

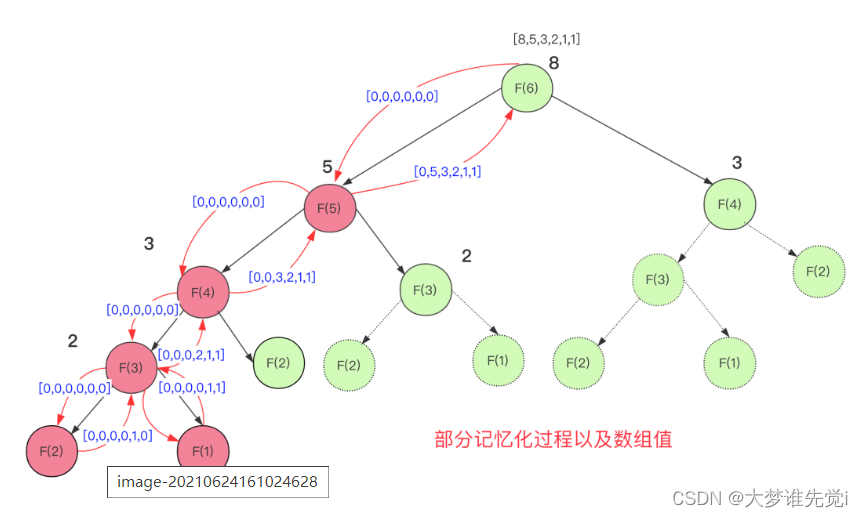
实现记忆化搜索求斐波那契代码为：

static long F(int n,long record[])
{
    
  if(n==1||n==2) {
    return 1;}
  if(record[n]>0)
    return record[n];
  else
    record[n]=F(n-1,record)+F(n-2,record);
  return record[n];
}
public static void main(String[] args) {
    
  int n=6;
  long[] record = new long[n+1];
  System.out.println(F(n,record));
}

而动态规划的方式你可以从前往后逻辑处理，从第三个开始每个dp都是前两个dp之和。

 public int fib(int n) {
    
        int dp[]=new int[n+1];
        dp[0]=0;
        dp[1]=1;
        for(int i=2;i<n+1;i++){
    
            dp[i]=dp[i-1]+dp[i-2];
        }
        return dp[n];
    }

当然动态规划也能有很多空间优化，有些只用一次的值，你可以用一些变量去替代。有些二维数组很大也可以用一维数组交替替代。当然动态规划专题很大，有很多比如树形dp、状压dp、背包问题等等经常出现在竞赛中，能力有限这里就将一些出现笔试高频的动态规划！

连续子数组最大和

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

示例:

输入: [-2,1,-3,4,-1,2,1,-5,4]
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。

dp的方法就是O(n)的方法。如果dp[i]表示以第i个结尾的最大序列和，而这个dp的状态方程为：

dp[0]=a[0]
dp[i]=max(dp[i-1]+a[i],a[i])

也不难解释，如果以前一个为截至的最大子序列和大于0，那么就连接本个元素，否则本个元素就自立门户。

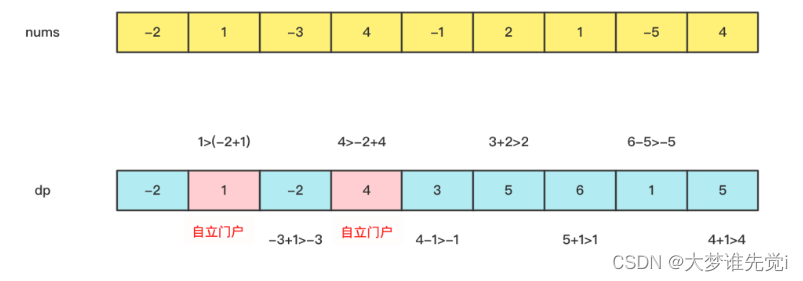
实现代码为：

public int maxSubArray(int[] nums) {
    
    int dp[]=new int[nums.length];
    int max=nums[0];
    dp[0]=nums[0];
    for(int i=1;i<nums.length;i++)
    {
    
      dp[i]=Math.max(dp[i-1]+nums[i],nums[i]);
      if(dp[i]>max)
        max=dp[i];
    }
    return max;
}

连续子数组最大乘积

给你一个整数数组 nums ，请你找出数组中乘积最大的连续子数组（该子数组中至少包含一个数字），并返回该子数组所对应的乘积。

示例 :

输入: [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6

。

连续子数组的最大乘积，这也是一道经典的动态规划问题，但是和普通动态规划又有点小不同。

如果数据中都是非负数，对于连续数组的最大乘积，那样处理起来和前面连续子数组最大和处理起来有些相似，要么和前面的叠乘，要么自立门户。

dp[0]=nums[0]
dp[i]=max(dp[i-1]*a[i],a[i])

但是这里面的数据会出现负数，乘以一个负数它可能从最大变成最小，并且还有负负得正就又可能变成最大了。

这时候该怎么考虑呢？

容易，我们开两个dp，一个dpmax[]记录乘积的最大值，一个dpmin[]记录乘积的最小值。然后每次都更新dpmax和dpmin不管当前值是正数还是负数.这样通过这两个数组就可以记录乘积的绝对值最大。

动态方程也很容易

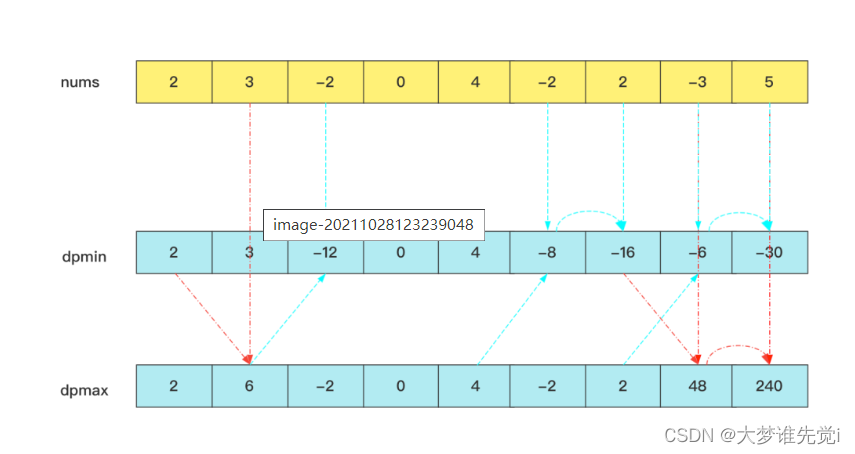
dpmax[i]=max(dpmax[i-1]*nums[i],dpmin[i-1]*nums[i],nums[i])
dpmin[i]=min(dpmax[i-1]*nums[i],dpmin[i-1]*nums[i],nums[i])

看一个过程就能理解明白，dpmin就是起到中间过度的作用，记录一些可能的负极值以防备用。结果还是dpmax中的值。

最长递增子序列

最长递增子序列，也称为LIS,是出现非常高频的动态规划算法之一。这里对应力扣300

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

输入：nums = [0,1,0,3,2,3]
输出：4
解释：最长递增子序列是 [0,1,2,3]，因此长度为 4 。

对于最长递增子序列，如果不考虑动态规划的方法，使用暴力枚举其实还是比较麻烦的，因为你不知道遇到比前面元素大的是否要递增。

比如 1 10 3 11 4 5，这个序列不能选取1 10 11而1 3 4 5才是最大的，所以暴力枚举所有情况的时间复杂度还是非常高的。

如果我们采取动态规划的方法，创建的dp[]数组，dp[i]表示以nums[i]结尾的最长递增子序列，而dp[i]的求解方式就是枚举i号前面的元素和对应结尾的最长子序列，找到一个元素值小于nums[i]并且递增序列最长，这样的时间复杂度为O(n2)。

状态转移方程为：

dp[i]=max(dp[j])+1, 其中0≤j<i且num[j]<num[i]

具体流程为：

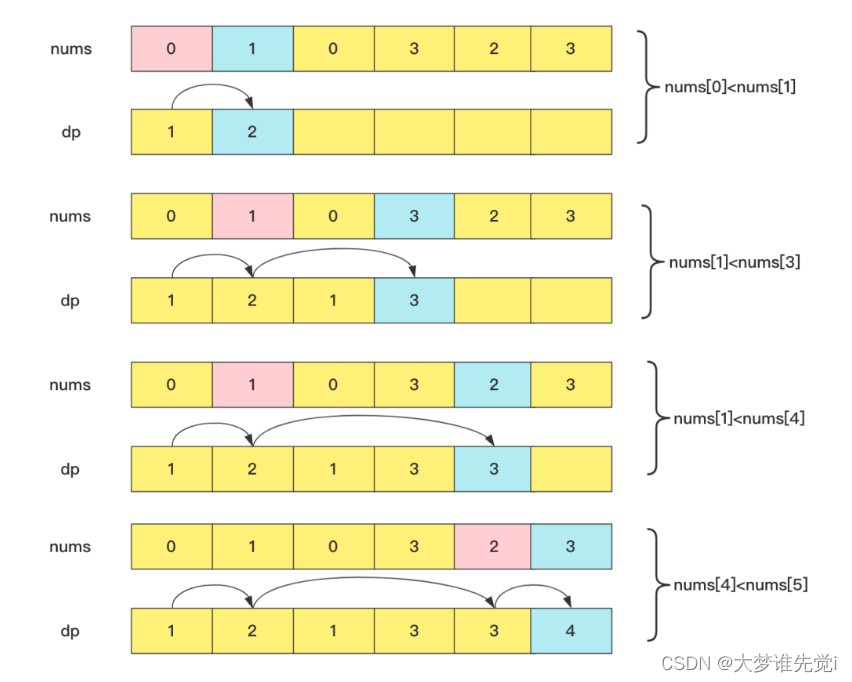
实现代码为：

class Solution {
    
    public int lengthOfLIS(int[] nums) {
    
        int dp[]=new int[nums.length];
        int maxLen=1;
        dp[0]=1;
        for(int i=1;i<nums.length;i++){
    
            int max=0;//统计前面 末尾数字比自己小 最长递增子串
            for(int j=0;j<i;j++){
    //枚举
                //结尾数字小于当前数字 并且长度大于记录的最长
                if(nums[j]<nums[i]&&dp[j]>max){
    
                    max=dp[j];
                }
            }
            dp[i]=max+1;//前面最长 加上自己
            if(maxLen<dp[i])
                maxLen=dp[i];
        }
        return maxLen;
    }
}

最长公共子序列

最长公共子序列也成为LCS.出现频率非常高！

给定两个字符串 text1 和 text2，返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ，返回 0 。

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

例如，“ace” 是 “abcde” 的子序列，但 “aec” 不是 “abcde” 的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。

拿b c d d e和 a c e e d e举例，其的公共子串为c d e。如果使用暴力，复杂度太高会直接超时，就需要使用动态规划。两个字符串匹配，我们设立二维dp[][]数组，dp[i][j]表示text1串第i个结尾，text2串第j个结尾的最长公共子串的长度。

这里核心就是要搞懂状态转移，分析dp[i][j]的转换情况，当到达i,j时候：

如果text1[i]==text2[j],因为两个元素都在最末尾的位置，所以一定可以匹配成功，换句话说，这个位置的邻居dp值不可能大于他（最多相等）。所以这个时候就是dp[i][j]=dp[i-1][j-1] +1;

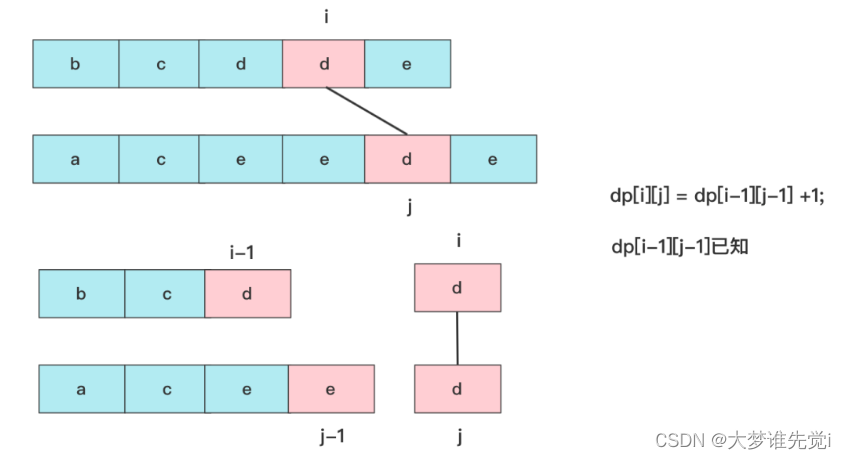
如果text1[i]!=text2[j]，就有两种可能性，我们知道的邻居有dp[i-1][j],dp[i][j-1]，很多人还会想到dp[i-1][j-1]这个一定比前两个小于等于，因为就是前面两个子范围嘛！所以这时就相当于末尾匹配不成，就要看看邻居能匹配的最大值啦，此时dp[i][j]=max(dp[i][j-1],dp[i-1][j])。

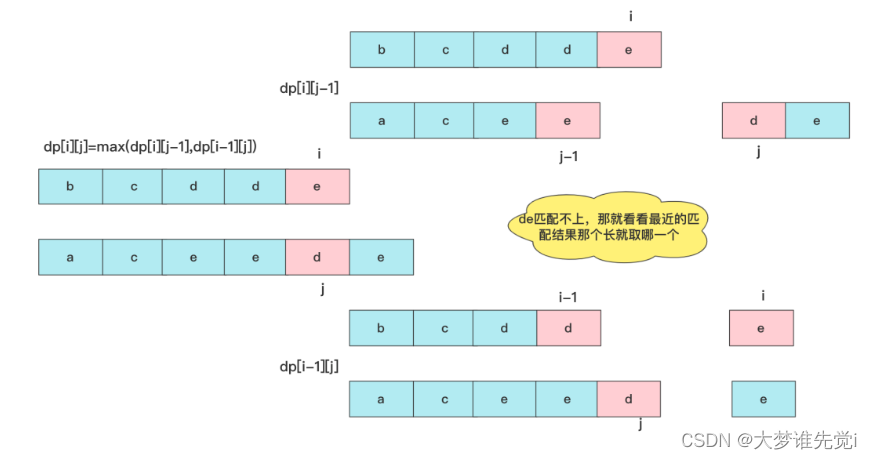
所以整个状态转移方程为：

dp[i][j] = dp[i-1][j-1] + 1            //text1[i]==text2[j]时
dp[i][j] = max(dp[i][j-1],dp[i-1][j])  //text1[i]!=text2[j]时

实现代码为：

class Solution {
    
    public int longestCommonSubsequence(String text1, String text2) {
    
        char ch1[]=text1.toCharArray();
        char ch2[]=text2.toCharArray();
        int dp[][]=new int[ch1.length+1][ch2.length+1];
        for(int i=0;i<ch1.length;i++)
        {
    
            for(int j=0;j<ch2.length;j++)
            {
    
                if(ch1[i]==ch2[j])
                {
    
                    dp[i+1][j+1]=dp[i][j]+1;
                }
                else
                    dp[i+1][j+1]=Math.max(dp[i][j+1],dp[i+1][j]);

            }
        }
        return dp[ch1.length][ch2.length];
    }
}

最长公共子串

给定两个字符串str1和str2,输出两个字符串的最长公共子串。

例如 abceef 和a2b2cee3f的最长公共子串就是cee。公共子串是两个串中最长连续的相同部分。

如何分析呢? 和上面最长公共子序列的分析方式相似，要进行动态规划匹配，并且逻辑上处理更简单，只要当前i,j不匹配那么dp值就为0，如果可以匹配那么就变成dp[i-1][j-1] + 1

核心的状态转移方程为：

dp[i][j] = dp[i-1][j-1] + 1            //text1[i]==text2[j]时
dp[i][j] = 0  //text1[i]!=text2[j]时

这里代码和上面很相似就不写啦，但是有个问题有的会让你输出最长字符串之类，你要记得用一些变量存储值。

不同子序列

不同子序列也会出现，并且有些难度，前面这篇不同子序列问题分析讲的大家可以看看。

给定一个字符串 s 和一个字符串 t ，计算在 s 的子序列中 t 出现的个数。

字符串的一个 子序列 是指，通过删除一些（也可以不删除）字符且不干扰剩余字符相对位置所组成的新字符串。（例如，“ACE” 是 “ABCDE” 的一个子序列，而 “AEC” 不是）

示例 ：

输入：s = "rabbbit", t = "rabbit"
输出：3
解释：
如下图所示, 有 3 种可以从 s 中得到 "rabbit" 的方案。
(上箭头符号 ^ 表示选取的字母)
rabbbit
^^^^ ^^
rabbbit
^^ ^^^^
rabbbit
^^^ ^^^

分析：
这个问题其实就是上面有几个pat的变形拓展，其基本思想其实是一致的，上面那题问的是有几个pat，固定、且很短。但这里面t串的长度不固定，所以处理上就要使用数组来处理而不能直接if else。

这题的思路肯定也是动态规划dp了，dp[j]的意思就是t串中[0,j-1]长字符在s中能够匹配的数量(当然这个值从前往后是动态变化的)，数组大小为dp[t.length+1]。在遍历s串的每一个元素都要和t串中所有元素进行对比看看是否相等，如果s串枚举到的这个串和t串中的第j个相等。那么dp[j+1]+=dp[j]。你可能会问为啥是dp[j+1],因为第一个元素匹配到需要将数量+1，而这里为了避免这样的判断我们将dp[0]=1,这样t串的每个元素都能正常的操作。

但是有一点需要注意的就是在遍历s串中第i个字母的时候，遍历t串比较不能从左向右而必须从右向左。因为在遍历s串的第i个字符在枚举dp数组时候要求此刻数据是相对静止的叠加(即同一层次不能产生影响)，而从左往右进行遇到相同字符会对后面的值产生影响。区别的话可以参考下图这个例子：

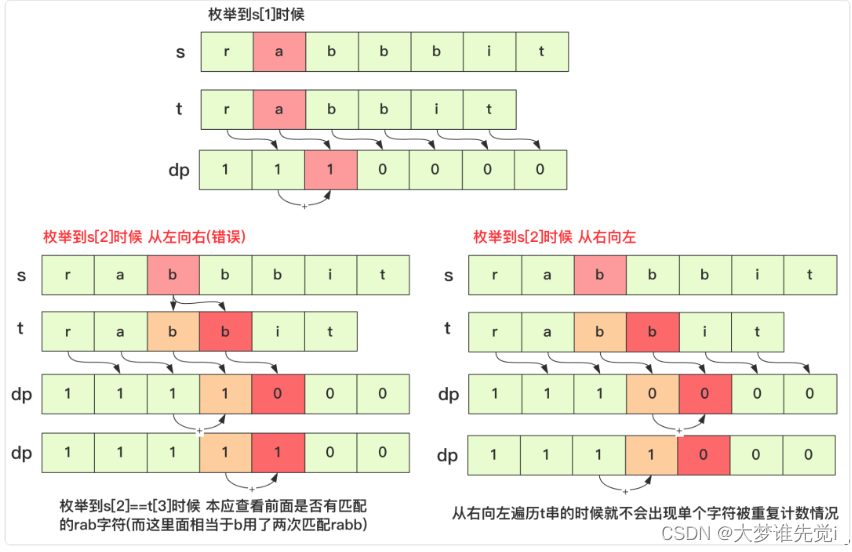
实现的代码为：

class Solution {
    
    public int numDistinct(String s, String t) {
    
      char s1[]=s.toCharArray();
      char t1[]=t.toCharArray();
      int dp[]=new int[t1.length+1];
      dp[0]=1;//用来叠加

      for(int i=0;i<s1.length;i++)
      {
    
        for(int j=t1.length-1;j>=0;j--)
        {
    
          if(t1[j]==s1[i])
          {
    
            dp[j+1]+=dp[j];
          }
        }
      }
      return dp[t1.length];
    }
}

结语

至此，简单的动态规划算是分享完了。

大部分简单动态规划还是有套路的，你看到一些数组问题、字符串问题很有可能就暗藏动态规划。动态规划的套路跟递归有点点相似，主要是找到状态转移方程，有时候考虑问题不能一步想的太多(想太多可能就把自己绕进去了)，而动态规划就是要大家对数值上下转换计算需要了解其中关系。