当前位置:网站首页>力扣刷题之有效的正方形(每日一题7/29)
力扣刷题之有效的正方形(每日一题7/29)
2022-08-03 19:01:00 【兰舟千帆】
力扣刷题之有效的正方形(每日一题7/29)
本题我采用的完全的计算暴力。
题目地址如下 链接
题目要求如下
给定2D空间中四个点的坐标 p1, p2, p3 和 p4,如果这四个点构成一个正方形,则返回 true 。 点的坐标 pi 表示为 [xi, yi] 。输入 不是 按任何顺序给出的。 一个 有效的正方形 有四条等边和四个等角(90度角)。 来源:力扣(LeetCode)
这是基本的要求。其实呢!提示我也没有去用,因为我采用的是完全的纯数学计算,用到了坐标的特点。比较暴力,代码快大,但是效率就是高。
下面是我的代码
class Solution {
public boolean validSquare(int[] p1, int[] p2, int[] p3, int[] p4) {
boolean result = judge_finally(p1,p2,p3,p4);
return result;
}
public static boolean judge_finally(int[]p1,int[]p2,int[]p3,int[]p4) {
double v_1_2 = judge_rhomb(p1, p2);//这里计算了一些可能用到的距离
double v2_3 = judge_rhomb(p2, p3);
double v3_4 = judge_rhomb(p3, p4);
double v1_4 = judge_rhomb(p1, p4);
double v_2_4 = judge_rhomb(p2, p4);
double v_1_3 = judge_rhomb(p1, p3);
//这里列出了可能构成的对角线,并作出对角线的判断,包括四点对角线中点重合,确认四边形
//距离相等以及对角线垂直约束。这样就逐步约束为正方形
//注意约束零点坐标,所以必须做一个约束,这里约束了对角线距离不为0
if (v_1_3 == v_2_4 && v_1_3 != 0&&judge_vertical(p1, p3, p2, p4)&judge_if_line(p1,p3,p2,p4)) {
return true;
}
if (v1_4 == v2_3 && v1_4 != 0&&judge_vertical(p1, p4, p2, p3)&judge_if_line(p1,p4,p2,p3)) {
return true;
}
if (v_1_2 == v3_4 && v_1_2 != 0&&judge_vertical(p1, p2, p3, p4)&judge_if_line(p1,p2,p3,p4)) {
return true;
}
return false;
}
public static double judge_rhomb(int[]a,int[]b)//计算两坐标构成线的长度
{
double x1 = ( Math.pow(a[0]-b[0],2)+Math.pow(a[1]-b[1],2));
return x1;
}
public static boolean judge_vertical(int[]a,int[]b,int[]c,int[]d)//判断直角
{
int v[] = {a[0]-b[0],a[1]-b[1]};
int v1[] = {c[0]-d[0],c[1]-d[1]};
return v[0]*v1[0]+v[1]*v1[1]==0;
}
public static boolean judge_if_line(int[]a,int[]b,int[]c,int[]d)//判断四点能否构成平行四边形
//如果四点可以构成平行四边形,则对角线中点重合
{
boolean bool_line_ = a[0] + b[0] == c[0] + d[0];
boolean bool_line__ = a[1]+b[1]==c[1]+d[1];
if (bool_line_&&bool_line__)
{
return true;
}
return false;
}
}归结方法,很基础的方法 调用判断。这里的垂直用到了向量的特点。 x1x2+y1y2=0,这样就可以判断是否垂直。 对坐标四点判断是否构成平行四边形,需要判断对可能情况的对角线的中点是否重合,那么这里只要分别计算横纵坐标死否分别相等就行。 菱形的对角线是互相垂直平分的,我们只要在让它的对角线相等,就可以判断为正方形。但是要注意做这些给出的坐标约束。所以我给了对角线长度不为0。因为如果四个点的横纵坐标都为0的话,上面的要求其实是都可以满足的。
完全的对对角线的约束。
边栏推荐
- 高等数学---第十章无穷级数---常数项级数
- MySQL——增删改查进阶
- WEB 渗透之RCE
- Protobuf Grpc使用异常 类型有未导出的方法,并且是在不同的软件包中定义
- 盲僧发现了华点——教你如何使用API接口获取数据
- POJ 2377 Bad Cowtractors(最大生成树)
- Confused!Ali was abused on the one hand, but was fortunate to be promoted to Huawei's technology, and successfully got the offer, with an annual salary of 40w
- 分享即时通讯开发之WebSocket:概念、原理、易错常识、动手实践
- MPLS的简单应用于实验
- 梅科尔工作室-14天华为培训七
猜你喜欢
随机推荐
ScrollView嵌套RV,滑动有阻力不顺滑怎么办?
MySQL如何 drop 大表
Online monitoring of UPS power supply and operating environment in the computer room, the solution is here
excel写入不完全sheet.append方法(openpyxl)
实时渲染器不止lumion,Chaos Vantage你值得一试
JumpServer开源堡垒机完成龙芯架构兼容性认证
MySQL【变量、流程控制与游标】
87. (Home of cesium) cesium heat map (topography)
[数据集][VOC]老鼠数据集voc格式3001张
MySQL详细学习教程(建议收藏)
阿里二面:多线程间的通信方式有几种?举例说明
ROS仿真环境搭建
[Azure Event Hub] Create Event Hub Consume Client + Custom Event Position with Azure AD Authentication
idea——同一项目开启多个实例(不同端口)
MySQL——增删改查进阶
阿里巴巴政委体系-第五章、阿里政委体系建设
C#将位图旋转90度
Postgresql中的pg_memory_barrier_impl和C的volatile
爬虫之selenium
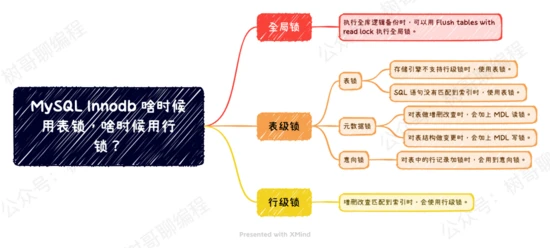
When does MySQL use table locks and when to use row locks?You should know this