Row and column differences in matrix construction of DX HLSL and GL glsl

---

Purpose

I've been doing some work recently DXBC to HLSL The job of , Some of them DX HLSL Medium mul(pos, matrix) and GL GLSL Medium mul(matrix, pos) The difference of

To make it easier to do shader reverse , So keep a record DX, GL Some of the differences in

---

problem

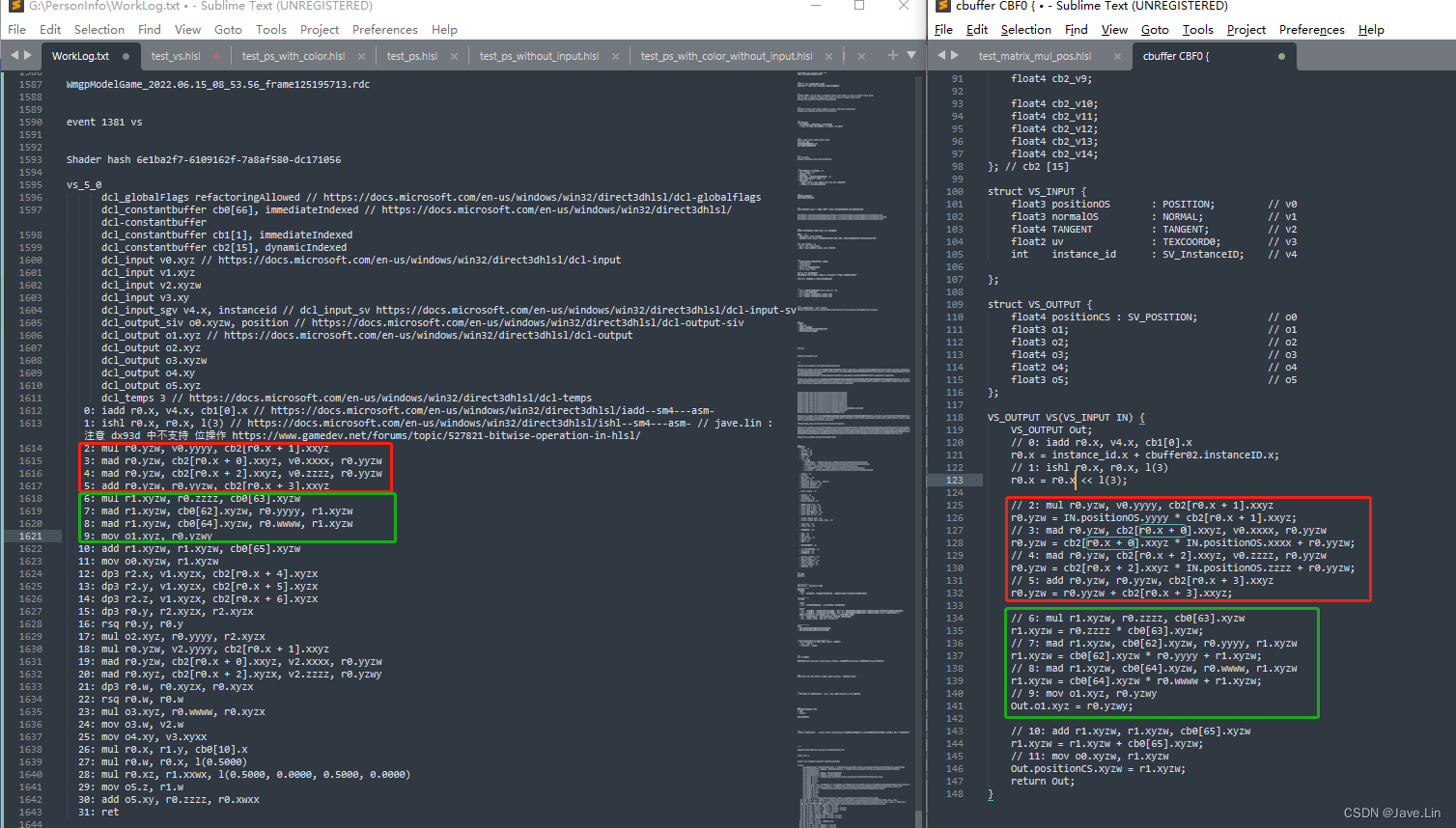
above In the red box and Green box The code in , I can probably see that Some matrix transformation operations

But revert to Corresponding HLSL when , Or see some HLSL Example time , Find out DX, GL Of mul The usage function Have lost lose Different

these DX And GL The difference is really annoying , Easy to forget , and Unity It uses column major The way To build the structure

But the operation is GL To build the matrix , I almost lost my mind ...

Write it down again , Otherwise, it's easy to forget 、 Mix up （ After all, I don't use it often Microsoft HLSL、FXC compiler ）

In the picture above A piece of code can actually be rewritten to correspond to HLSL in mul(floatN, matrixNxN)

	// 2: mul r0.yzw, v0.yyyy, cb2[r0.x + 1].xxyz
	r0.yzw = IN.positionOS.yyyy * cb2[r0.x + 1].xxyz;
	// 3: mad r0.yzw, cb2[r0.x + 0].xxyz, v0.xxxx, r0.yyzw
	r0.yzw = cb2[r0.x + 0].xxyz * IN.positionOS.xxxx + r0.yyzw;
	// 4: mad r0.yzw, cb2[r0.x + 2].xxyz, v0.zzzz, r0.yyzw
	r0.yzw = cb2[r0.x + 2].xxyz * IN.positionOS.zzzz + r0.yyzw;
	// 5: add r0.yzw, r0.yyzw, cb2[r0.x + 3].xxyz
	r0.yzw = r0.yyzw + cb2[r0.x + 3].xxyz;

	// jave.lin :  above  2~5 lines Of  DXBC  The code analysis , Can be equivalent to 
	float4x4 matrixL2W = {
     // jave.lin : local to world matrix
		cb2[r0.x + 0].xxyz,  // jave.lin :  New coordinate base :x Axis 
		cb2[r0.x + 1].xxyz,  // jave.lin :  New coordinate base :Y Axis 
		cb2[r0.x + 2].xxyz,  // jave.lin :  New coordinate base :Z Axis 
		cb2[r0.x + 3].xxyz   // jave.lin :  Radially transformed  xyz  Translation 
	};
	r0.yzw = mul(float4(IN.positionOS, 1.0), matrixL2W);

From here DXBC It looks good , Because I used to GL Medium Matrix left multiplication , But it's written HLSL Words , We need to pay attention to DX and GL The difference between

I'm on my own excel Some pictures are drawn to summarize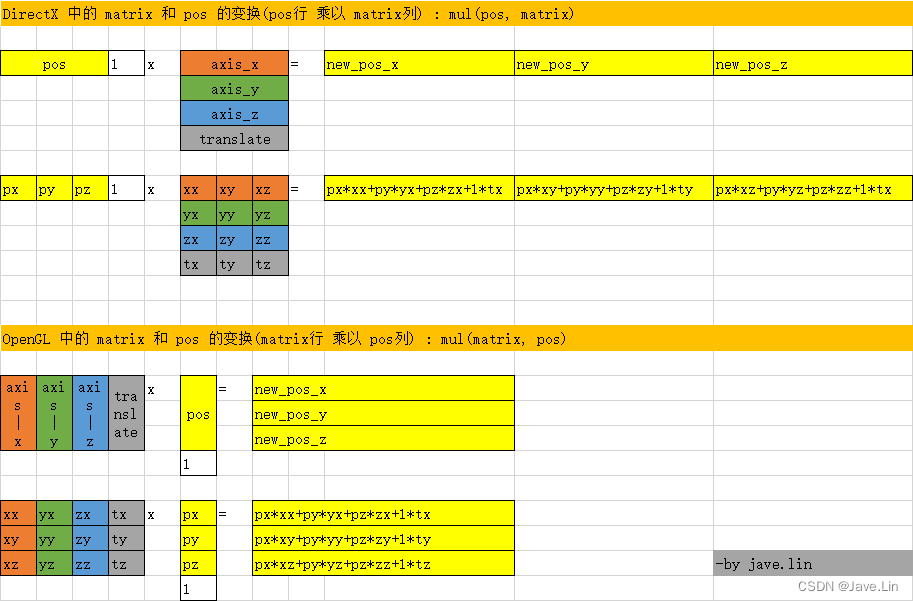

OpenGL Medium matrix[0] What is taken is Column
DirectX Medium matrix[0] What is taken is That's ok

Here are some sample code , and official One or two paragraphs describe and Code

---

show me the code, talk is cheap.

---

Example

OpenGL:

vec3 pos = ...;
mat3x3 model_mat = mat3x3(
	vec3(0,0,0), // column 1
	vec3(1,1,1), // column 2
	vec3(2,2,2), // column 3
	);
vec3 posWS = mul(model_mat, pos); // model_mat  That's ok   ride  pos  Column 

DirectX:

float3 pos = ...;
float3x3 model_mat = {
    
	0, 0, 0, // row 1
	1, 1, 1, // row 2
	2, 2, 2  // row 3
};
float3 posWS = mul(pos, model_mat); // pos  That's ok   ride  model_mat  Column 

---

file

Let's refer to ：DirectX Medium matrix type Of Component operation ：Per-Component Math Operations - matrix type

---

Overloaded versions of the multiply intrinsic function handle cases where one operand is a vector and the other operand is a matrix. Such as: vector * vector, vector * matrix, matrix * vector, and matrix * matrix. For instance:

float4x3 World;

float4 main(float4 pos : SV_POSITION) : SV_POSITION
{
    
    float4 val;
    val.xyz = mul(pos,World);
    val.w = 0;

    return val;
}

produces the same result as:

float4x3 World;

float4 main(float4 pos : SV_POSITION) : SV_POSITION
{
    
    float4 val;
    val.xyz = (float3) mul((float1x4)pos,World);
    val.w = 0;

    return val;
}

This example casts the pos vector to a column vector using the (float1x4) cast. Changing a vector by casting, or swapping the order of the arguments supplied to multiply is equivalent to transposing the matrix.

Automatic cast conversion causes the multiply and dot intrinsic functions to return the same results as used here:

{
    
  float4 val;
  return mul(val,val);
}

This result of the multiply is a 1x4 * 4x1 = 1x1 vector. This is equivalent to a dot product:

{
    
  float4 val;
  return dot(val,val);
}

---

References

• DirectX Medium matrix type Of Component operation ：Per-Component Math Operations - matrix type