当前位置:网站首页>完全背包问题的思路解析
完全背包问题的思路解析
2022-08-03 10:45:00 【hnjzsyjyj】
【算法分析】
背包问题,求解的是“将某些种物品装入背包,......”,而不是求解“将某些个物品装入背包,......”的问题。切记。
完全背包问题,类似于0-1背包问题,依然是求解“将哪些种物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大”。故依然可设 c[i][j] 为将前 i 种物品装入容量为 j 的背包中所获得的最大价值,vol[i] 为第 i 中物品的体积,val[i] 为第 i 种物品的价值。但由于其特殊性,即在完全背包问题中的每种物品有无限多个,而0-1背包问题中的每种物品只有一个,故在利用“最后一步法”构建完全背包问题的状态转移方程时,针对第 i 种物品,可能会选择0,1,2,... ,k个(k*vol[i]<=j)。之所以会选到 k 个,而不是无限多个,原因在于虽然完全背包问题中每种物品都有无限多个,但受到背包容量的限制,只可能装有限个。
完全背包问题的视频讲解可参考:https://www.bilibili.com/video/BV16F411M7CU
思路详见下图:

可见依据上图的分析思路,则完全背包问题的代码将会有三重循环,必然导致代码复杂度增加。同时,这也必然会导致时间复杂度剧增,有可能会TLE。因此,需要进行优化。
将完全背包问题的状态转移方程写在下方:
c[i][j]=max(c[i-1][j],c[i-1][j-vol[i]]+val[i], ..., c[i-1][j-(k-1)*vol[i]]+(k-1)*val[i], c[i-1][j-k*vol[i]]+k*val[i]),令 j=j-vol[i],并考虑到 k*vol[i]<=j,则有
c[i][j-vol[i]]=max(c[i-1][j-vol[i]],c[i-1][j-vol[i]-vol[i]]+val[i], ..., c[i-1][j-vol[i]-(k-1)*vol[i]]+(k-1)*val[i])
=max(c[i-1][j-vol[i]],c[i-1][j-2*vol[i]]+val[i], ..., c[i-1][j-k*vol[i]]+(k-1)*val[i])
推出完全背包问题的状态转移方程 c[i][j]=max(c[i-1][j], c[i][j-vol[i]]+val[i]),这样就优化为二维了。
类比于0-1背包问题的状态转移方程 c[i][j]=max(c[i-1][j],c[i-1][j-vol[i]]+val[i]) 优化为一维的思路,可在上面优化为二维的基础上,进一步得出完全背包问题的一维优化形式:
c[j]=max(c[j], c[j-vol[i]]+val[i]),满足 i:1~n,j:1~V 且 j>=vol[i]
若要从代码模板的角度来看的话,完全背包问题的代码只需要将0-1背包问题的一维实现代码的内层循环改为从 vol 到 V 进行遍历便可。即将0-1背包问题的一维实现中的内层循环 for(int j=V;j>=vol;j--) 改为 for(int j=vol;j<=V;j++) ,便为完全背包的代码实现。是不是有点废O(∩_∩)O哈哈~
【算法代码】
#include<bits/stdc++.h>
using namespace std;
const int maxn=1005;
int c[maxn];
int main() {
int n,V;
cin>>n>>V;
for(int i=1;i<=n;i++){
int vol,val;
cin>>vol>>val;
for(int j=vol;j<=V;j++)
c[j]=max(c[j],c[j-vol]+val);
}
cout<<c[V]<<endl;
return 0;
}
/*
in:
4 5
1 2
2 4
3 4
4 5
out:
10
*/
【参考文献】
https://blog.csdn.net/hnjzsyjyj/article/details/126126183
https://www.bilibili.com/video/BV16F411M7CU
https://www.acwing.com/problem/content/description/3/
https://blog.csdn.net/hnjzsyjyj/article/details/125987923
边栏推荐
- How to deal with this time of MySQL binlog??
- 深度学习100例——卷积神经网络(CNN)实现服装图像分类
- 罕见的数学天才,靠“假结婚”才得到追求事业的机会
- 孙宇晨式“溢价逻辑”:不局限眼前,为全人类的“星辰大海”大胆下注
- Interview Blitz 71: What's the difference between GET and POST?
- Depth study of 100 cases - convolution neural network (CNN) to realize the clothing image classification
- 分布式事务七种解决方案
- 跨链桥协议 Nomad 遭遇黑客攻击,损失超 1.5 亿美元
- ScrollView嵌套RecyclerView滚动冲突
- 安全研究员:大量Solana钱包被盗
猜你喜欢
Machine Learning Overview

STM32+OLED显示屏制作指针式电子钟
Depth study of 100 cases - convolution neural network (CNN) to realize the clothing image classification
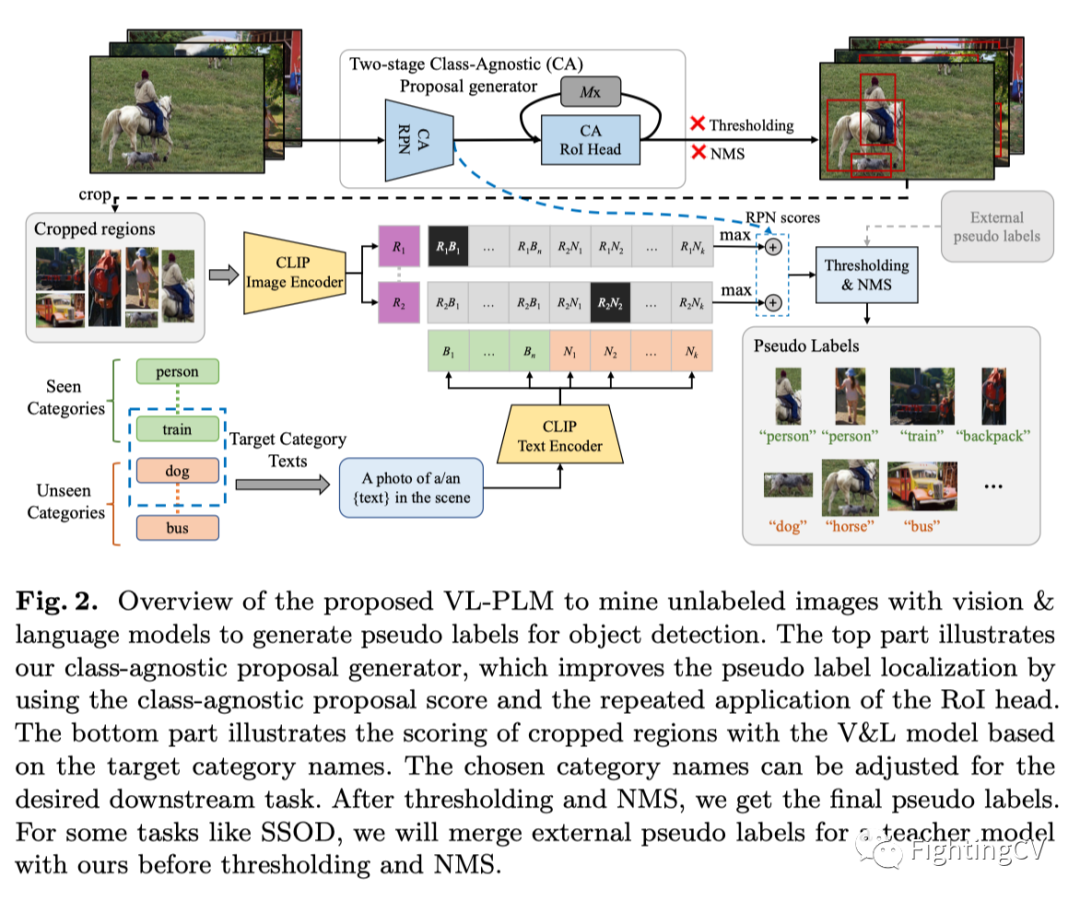
ECCV2022 | RU&谷歌:用CLIP进行zero-shot目标检测!

type=“module“ 你了解,但 type=“importmap“ 你知道吗
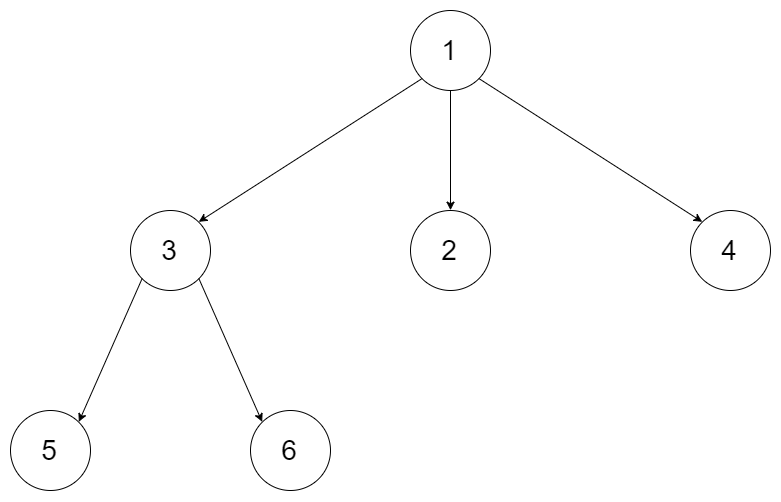
LeetCode_多叉树_中等_429.N 叉树的层序遍历
鸿蒙第三次

投稿有礼,双社区签约博主名额等你赢!
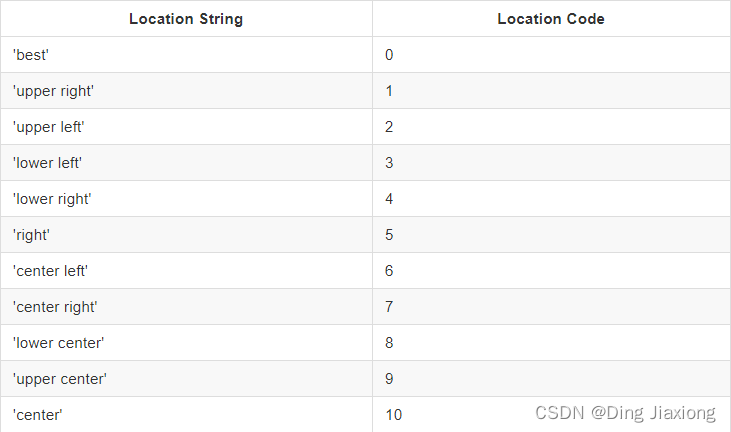
Matplotlib
开源一夏 | 教你快速实现“基于Docker快速构建基于Prometheus的MySQL监控系统”
随机推荐
玉溪卷烟厂通过正确选择时序数据库 轻松应对超万亿行数据
Leecode-SQL 1484. 按日期分组销售产品
This article understands the process from RS485 sensor to IoT gateway to cloud platform
GBase 8c与openGauss是什么关系?
509. 斐波那契数
在 Chrome 开发者工具里通过 network 选项模拟网站的离线访问模式
成对连接点云分割
4 g acquisition ModbusTCP turn JSON MQTT cloud platform
集成学习、boosting、bagging、Adaboost、GBDT、随机森林
LeetCode第三题(Longest Substring Without Repeating Characters)三部曲之二
鸿蒙第四次
C# Color颜色RGB对照表、颜色选择器
三大产品力赋能欧萌达OMODA5
关于OPENSSL的问题
跨域问题的分析
科普大佬说 | 黑客帝国与6G有什么关系?
Pixel mobile phone system
Machine Learning Overview
4G采集ModbusTCP转JSON接MQTT云平台
有大佬用flink读取mysql binlog分表后再写入新表吗