当前位置:网站首页>Simpson's paradox
Simpson's paradox
2022-08-02 00:16:00 【Zhang Chuncheng】
辛普森悖论
There is an amazing paradox in statistics,It's called Simpson's paradox(Simple’s Paradox).
简单来说,就是“在分组比较中都占优势的一方,In the overall evaluation, it is sometimes the loser.”
This paper attempts to adopt an interactive visualization method,explain it.
And trying to illustrate this paradoxical situation is not very out of the way,Even with proper construction methods,This kind of conflict can always happen.
辛普森悖论
This is a serious statistical problem,A detailed discussion can be found here
Simpson’s Paradox (Stanford Encyclopedia of Philosophy)[1]

Interactive chart explanation
本文的代码可见我的 OBSERVABLE codebook
Interactive Simpson's Paradox[2]

Raw data starts with OA 和 AB 的形式获得.The slope of the line segment refers to the precision,比例等.因此,OB The slope refers to the overall accuracy.
通常情况下,We want the slope to be as large as possible.
In the presence of the red triangle,It is easy to obtain a slope greater than OA的“更好”的OC方法.之后,can always be doneCD与AB平行.It's not hard to find this time,CD The slope of and AB 相等.
Then you can always find a ratio CD 更好的 CE,只要满足 CE 大于 CD 即可.
这时,射线 CE 与 OB There are always intersections,在 C Pick any point on the line segment between the point and the intersection O‘,This is obviously a comparisonOB更糟糕的OO'.
但是考虑到 OO’ 是由 OC 和 CE 生成的,However, in terms of slope,
OC 优于 OA CE 优于 AB 但 OO’ 劣于 OB
这就是辛普森悖论.
有意思的是,My previous derivation was from the red triangle OAB 开始,as long as this triangle exists,The existence interval of the paradox must be deduced OCO’.
也就是说,Regardless of the grouping of the group comparisons,We can always“生成”A new set of data,来“导致”Paradox occurs.
This shows that Simpson's paradox is not a special case of a corner,But as long as there are group comparisons,may appear“一般情况”.
参考资料
Simpson’s Paradox (Stanford Encyclopedia of Philosophy): https://plato.stanford.edu/entries/paradox-simpson/#:~:text=Simpson%E2%80%99s%20Paradox%20is%20a%20statistical%20phenomenon%20where%20an,independent%20or%20even%20negatively%20associated%20in%20all%20subpopulations.
[2]Interactive Simpson's Paradox: https://observablehq.com/@listenzcc/interactive-simpsons-paradox
边栏推荐
- 认识USB、Type-C、闪电、雷电接口
- IP核:FIFO
- Short video seo search optimization main content
- asyncawait和promise的区别
- SphereEx苗立尧:云原生架构下的Database Mesh研发实践
- Zadig 面向开发者的自测联调子环境技术方案详解
- 【MySQL系列】 MySQL表的增删改查(进阶)
- 洞见云原生微服务及微服务架构浅析
- security CSRF漏洞保护
- After an incomplete recovery, the control file has been created or restored, the database must be opened with RESETLOGS, interpreting RESETLOGS.
猜你喜欢
随机推荐
JSP Taglib指令具有什么功能呢?
Bean的生命周期
DOM 基础操作
一篇永久摆脱Mysql时区错误问题,idea数据库可视化插件配置
零基础如何学习单片机,一位入门者的进阶路径,可参考
TCP 可靠吗?为什么?
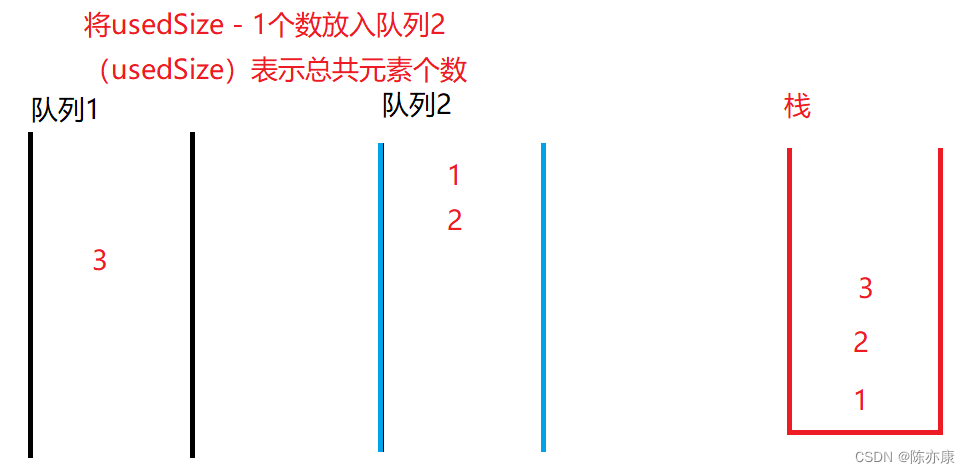
利用“栈”快速计算——逆波兰表达式
Short video SEO optimization tutorial Self-media SEO optimization skills and methods
Short video SEO search operation customer acquisition system function introduction
QML包管理
els block deformation
带你搞懂MySQL隔离级别,两个事务同时操作同一行数据会怎样?
Flink Yarn Per Job - 提交流程一
学习英语的网站与资料
els 长条变形
【解决】win10下emqx启动报错Unable to load emulator DLL、node.db_role = EMQX_NODE__DB_ROLE = core
Win11如何获得最佳电源效率?
回顾历史5次经济衰退时期:这一次可能会有何不同?
在linux下MySQL的常用操作命令
工件SSMwar exploded 部署工件时出错。请参阅服务器日志了解详细信息