当前位置:网站首页>[combinatorics] generating function (commutative property | derivative property | integral property)
[combinatorics] generating function (commutative property | derivative property | integral property)
2022-07-03 17:55:00 【Programmer community】
List of articles
- One 、 The commutative property of generating function
- Two 、 Derivation property of generating function
- 3、 ... and 、 Integral property of generating function
Reference blog :
- 【 Combinatorial mathematics 】 Generating function Brief introduction ( Generating function definition | Newton's binomial coefficient | Common generating functions | Related to constants | Related to binomial coefficient | Related to polynomial coefficients )
- 【 Combinatorial mathematics 】 Generating function ( Linear properties | Product properties )
- 【 Combinatorial mathematics 】 Generating function ( Shift property )
- 【 Combinatorial mathematics 】 Generating function ( The nature of summation )
One 、 The commutative property of generating function
Summation property of generating function 1 :
b
n
=
α
n
a
n
b_n = \alpha^n a_n
bn=αnan , be
B
(
x
)
=
A
(
α
x
)
B(x) =A( \alpha x)
B(x)=A(αx)
The sequence
a
n
a_n
an The generating function of is
A
(
x
)
A(x)
A(x) , The sequence
b
n
b_n
bn The generating function of is
B
(
x
)
B(x)
B(x) ,
The sequence
a
n
=
{
a
0
,
a
1
,
a
2
,
⋯
}
a_n = \{ a_0 , a_1, a_2 , \cdots \}
an={ a0,a1,a2,⋯} , The sequence
b
n
=
{
α
0
a
0
,
α
1
a
1
,
α
2
a
2
,
⋯
}
b_n = \{ \alpha^0a_0 , \alpha^1a_1, \alpha^2a_2 , \cdots \}
bn={ α0a0,α1a1,α2a2,⋯} ;
The sequence
a
n
a_n
an The generating function of
A
(
x
)
=
a
0
x
0
+
a
1
x
+
a
2
x
2
+
⋯
A(x) = a_0x^0 + a_1x + a_2x^2 + \cdots
A(x)=a0x0+a1x+a2x2+⋯
The sequence
b
n
b_n
bn The generating function of
B
(
x
)
=
α
0
a
0
x
0
+
α
1
a
1
x
1
+
α
2
a
2
x
2
+
⋯
B(x) = \alpha^0a_0x^0 + \alpha^1a_1x^1 + \alpha^2a_2x^2 + \cdots
B(x)=α0a0x0+α1a1x1+α2a2x2+⋯
Method of proof :
stay
b
n
b_n
bn The generating function of
B
(
x
)
B(x)
B(x) in , take
α
0
x
0
\alpha^0x^0
α0x0 As an item , take
α
1
x
1
\alpha^1x^1
α1x1 As an item , take
α
2
x
2
\alpha^2x^2
α2x2 As an item ,
By observing the above items, we can see ,
α
\alpha
α And
x
x
x The power of is the same ,
So you can take
α
x
\alpha x
αx As a variable ,
In this way, you can get
B
(
x
)
=
A
(
α
x
)
B(x) =A( \alpha x)
B(x)=A(αx) The formula ;
Two 、 Derivation property of generating function
Derivation property of generating function :
b
n
=
n
a
n
b_n = n a_n
bn=nan , be
B
(
x
)
=
x
A
′
(
x
)
B(x) =xA'( x)
B(x)=xA′(x)
The sequence
a
n
a_n
an The generating function of is
A
(
x
)
A(x)
A(x) , The sequence
b
n
b_n
bn The generating function of is
B
(
x
)
B(x)
B(x) ,
The sequence
a
n
=
{
a
0
,
a
1
,
a
2
,
⋯
,
a
n
,
⋯
}
a_n = \{ a_0 , a_1, a_2 , \cdots , a_n , \cdots \}
an={ a0,a1,a2,⋯,an,⋯} , The sequence
b
n
=
{
0
a
0
,
a
1
,
2
a
2
,
⋯
,
n
a
n
,
⋯
}
b_n = \{ 0a_0 , a_1, 2a_2 , \cdots, na_n ,\cdots \}
bn={ 0a0,a1,2a2,⋯,nan,⋯} ;
The sequence
a
n
a_n
an The generating function of
A
(
x
)
=
a
0
x
0
+
a
1
x
+
a
2
x
2
+
⋯
+
a
n
x
n
+
⋯
A(x) = a_0x^0 + a_1x + a_2x^2 + \cdots + a_nx^n + \cdots
A(x)=a0x0+a1x+a2x2+⋯+anxn+⋯
The sequence
b
n
b_n
bn The generating function of
B
(
x
)
=
0
a
0
x
0
+
1
a
1
x
1
+
2
a
2
x
2
+
⋯
+
n
a
n
x
n
+
⋯
B(x) = 0a_0x^0 + 1a_1x^1 + 2a_2x^2 + \cdots + na_nx^n + \cdots
B(x)=0a0x0+1a1x1+2a2x2+⋯+nanxn+⋯
Prove the above properties :
take The sequence
a
n
a_n
an The generating function of
A
(
x
)
A(x)
A(x) Derivation , Again multiply
x
x
x , You can get
B
(
x
)
B(x)
B(x) ;
A
(
x
)
=
a
0
x
0
+
a
1
x
+
a
2
x
2
+
⋯
+
a
n
x
n
+
⋯
A(x) = a_0x^0 + a_1x + a_2x^2 + \cdots + a_nx^n + \cdots
A(x)=a0x0+a1x+a2x2+⋯+anxn+⋯
Use derivative formula :
(
x
n
)
′
=
n
x
n
−
1
(x^n)' = nx^{n-1}
(xn)′=nxn−1
Reference resources : Derivation - Baidu Encyclopedia
A
′
(
x
)
=
0
+
a
1
+
2
a
2
x
+
⋯
+
n
a
n
x
n
−
1
+
⋯
A'(x) = 0 + a_1 + 2a_2x + \cdots + na_nx^{n-1} + \cdots
A′(x)=0+a1+2a2x+⋯+nanxn−1+⋯
x
A
′
(
x
)
=
0
+
a
1
x
+
2
a
2
x
2
+
⋯
+
n
a
n
x
n
+
⋯
=
B
(
x
)
xA'(x) = 0 + a_1x + 2a_2x^2 + \cdots + na_nx^{n} + \cdots = B(x)
xA′(x)=0+a1x+2a2x2+⋯+nanxn+⋯=B(x)
3、 ... and 、 Integral property of generating function
b
n
=
a
n
n
+
1
b_n = \cfrac{a_n}{n+1}
bn=n+1an , be
B
(
x
)
=
1
x
∫
0
x
A
(
x
)
d
x
B(x) =\cfrac{1}{x} \int^{x}_{0} A( x)dx
B(x)=x1∫0xA(x)dx
The above properties are hard to remember , Generate functions from known , Unknown generating functions can be derived , You can deduce when using ;
边栏推荐
- (9) Opencv Canny edge detection
- As soon as we enter "remote", we will never regret, and several people will be happy and several people will be sad| Community essay solicitation
- 远程办公工具分享|社区征文
- OpenSSL的SSL/BIO_get_fd
- i++与++i的区别:通俗易懂的讲述他们的区别
- Remote office tools sharing | community essay solicitation
- 面试官:值为 nil 为什么不等于 nil ?
- [combinatorics] generating function (linear property | product property)
- QT adjust win screen brightness and sound size
- Stm32h7 Hal library SPI DMA transmission has been in busy solution
猜你喜欢
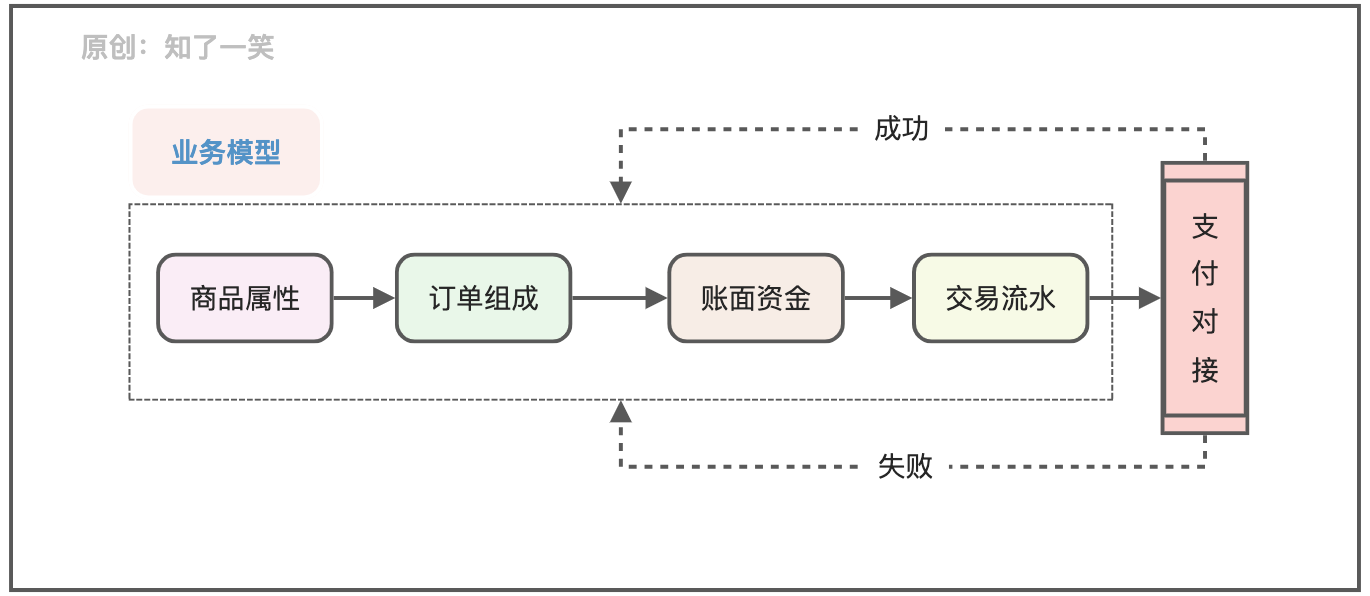
聊聊支付流程的設計與實現邏輯
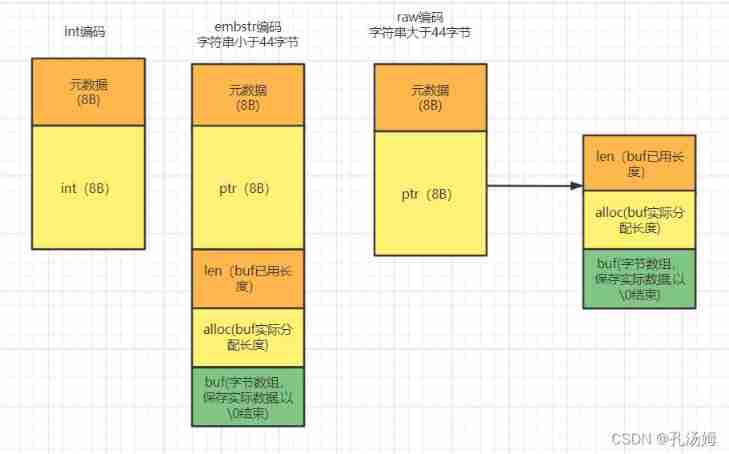
Redis core technology and practice - learning notes (11): why not just string

SQL injection database operation foundation

(9) Opencv Canny edge detection
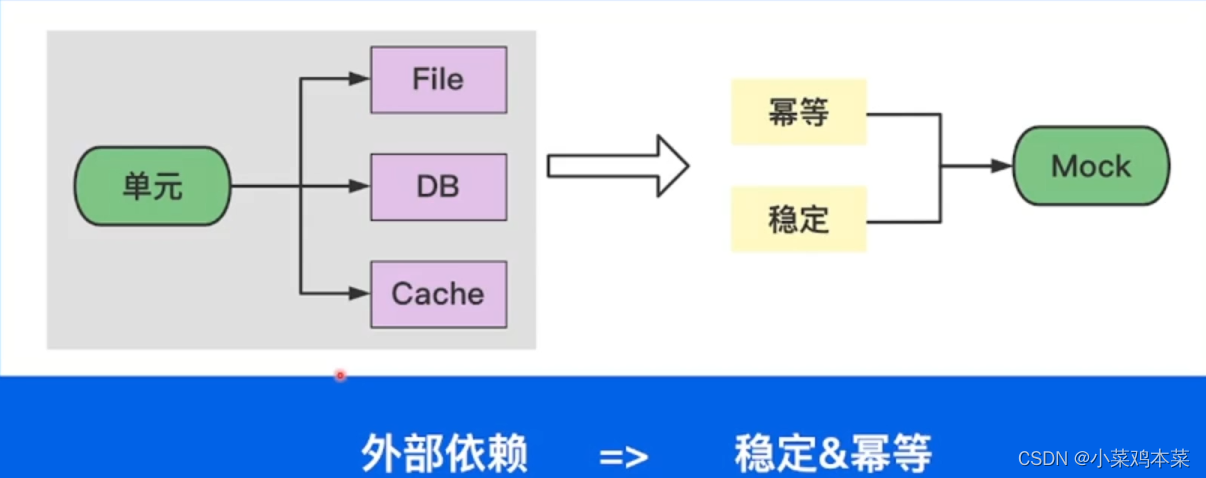
Golang unit test, mock test and benchmark test

Research Report on market demand and investment planning for the development of China's office chair industry, 2022-2028
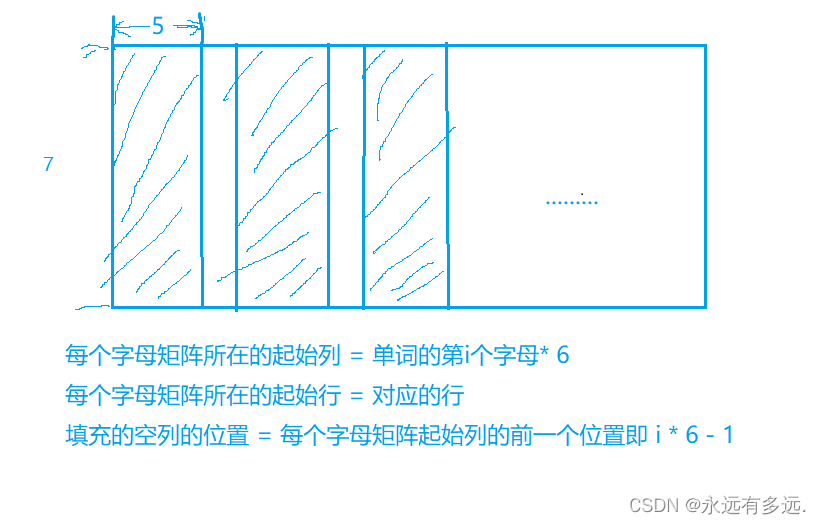
1164 Good in C

Vs2013 has blocked the installer, and ie10 needs to be installed

Redis core technology and practice - learning notes (VII) sentinel mechanism
Internet Hospital his Management Platform source, online Inquiry, appointment Registration Smart Hospital Small program source
随机推荐
A. Odd Selection【BruteForce】
TCP congestion control details | 3 design space
Five problems of database operation in commodity supermarket system
PHP MySQL inserts data
Managing multiple selections with MVVM - managing multiple selections with MVVM
[mathematical logic] equivalent calculus and reasoning calculus of predicate logic (individual word | predicate | quantifier | predicate logic formula | two basic formulas | proposition symbolization
[combinatorics] generating function (summation property)
1147_ Makefile learning_ Target files and dependent files in makefile
A. Odd Selection【BruteForce】
The difference between i++ and ++i: tell their differences easily
STM32实现74HC595控制
Fedora 21 安装 LAMP 主机服务器
Vs2013 has blocked the installer, and ie10 needs to be installed
As soon as we enter "remote", we will never regret, and several people will be happy and several people will be sad| Community essay solicitation
Leetcode 669 pruning binary search tree -- recursive method and iterative method
Servlet specification Part II
Internet hospital his management platform source code, online consultation, appointment registration smart hospital applet source code
Keepalived 设置不抢占资源
Leetcode540: a single element in an ordered array
Win32: dump file analysis of heap corruption