Leetcode 538 converts binary search tree into cumulative tree -- recursive method and iterative method

source ： Power button （LeetCode）
link ：https://leetcode-cn.com/problems/convert-bst-to-greater-tree

---

The question ：

Give a binary Search for Root node of tree , The node values of the tree are different , Please convert it to an accumulation tree （Greater Sum Tree）, Make each node node The new value of is equal to or greater than in the original tree node.val The sum of the values of .

As a reminder , The binary search tree satisfies the following constraints ：

The left subtree of a node contains only the key Less than Node key node .
The right subtree of a node contains only the key Greater than Node key node .
Left and right subtrees must also be binary search trees .
Be careful ： This topic and 1038: https://leetcode-cn.com/problems/binary-search-tree-to-greater-sum-tree/ identical

Example 1：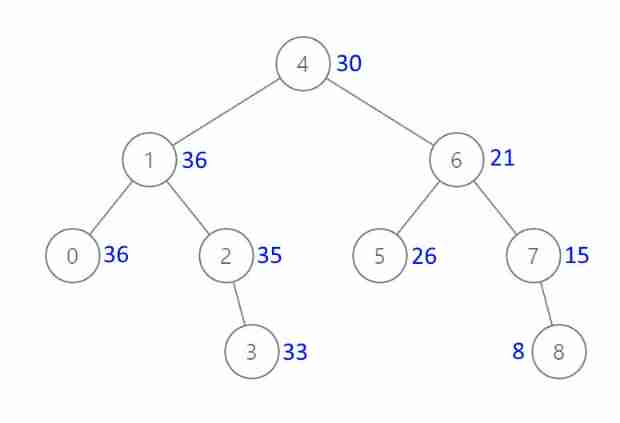

Input ：[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
Output ：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

Example 2：
Input ：root = [0,null,1]
Output ：[1,null,1]

Example 3：
Input ：root = [1,0,2]
Output ：[3,3,2]

Example 4：
Input ：root = [3,2,4,1]
Output ：[7,9,4,10]

Tips ：
The number of nodes in the tree is between 0 and 10⁴ Between .
The value of each node is between -10⁴ and 10⁴ Between .
All the values in the tree Different from each other .
The given tree is a binary search tree .

---

Reference article

Ideas ：

Code Capriccio recorded in 《 Binary tree ： Conclusion ！》 The summary written in it is very good , I'll post it here ：

• It involves the construction of binary tree , Whether ordinary binary tree or binary search tree, there must be a preamble , All nodes are constructed first .
• Find the properties of ordinary binary tree , Generally, it is a post order , It is usually calculated by the return value of recursive function .
• Find the properties of binary search tree , It must be the middle order , Or you'll be blind to order .

Because this problem involves the evaluation of binary search tree attributes , So we use middle order traversal to do , But the middle order traversal of this problem is a special middle order traversal .

In fact, this problem is not difficult , As long as you understand the idea, it is very simple ！

Mention binary search tree , Think immediately Using middle order traversal on binary search tree will get an ordered sequence , And what this topic says is accumulation （ Make each node node The new value of is equal to or greater than in the original tree node.val The sum of the values of .）, In fact, it is to add the value of each node In this ordered sequence, the sum of all numbers after the corresponding value of the current node .

After understanding this idea , In fact, we traverse the binary search tree in reverse order （ That is, first traverse the right node , Then traverse the intermediate nodes , Finally, traverse the left node ）, And this process uses a sum The current value can be superimposed by the variable .

We use iteration and recursion to do this problem respectively , Are to achieve the binary tree in the order of traversal （ Reverse order ）.

Recursive method Java Code ：

class Solution {
    
    int sum;
    private void search(TreeNode node) {
    
        if (node == null) return;
        search(node.right);
        node.val += sum;
        sum = node.val;
        search(node.left);
    }
    public TreeNode convertBST(TreeNode root) {
    
        search(root);
        return root;
    }
}

Iterative method Java Code ：

class Solution {
    
    public TreeNode convertBST(TreeNode root) {
    
        TreeNode cur = root;
        int sum = 0;
        Deque<TreeNode> deque = new LinkedList<>();
        while (cur != null || !deque.isEmpty()) {
    
            if (cur != null) {
    
                deque.push(cur);
                cur = cur.right;
            } else {
    
                cur = deque.poll();
                cur.val += sum;
                sum = cur.val;
                cur = cur.left;
            }
        }
        return root;
    }
}