当前位置:网站首页>[combinatorics] recursive equation (special solution example 1 Hannover tower complete solution process | special solution example 2 special solution processing when the characteristic root is 1)
[combinatorics] recursive equation (special solution example 1 Hannover tower complete solution process | special solution example 2 special solution processing when the characteristic root is 1)
2022-07-03 17:16:00 【Programmer community】
List of articles
- One 、 Special solution example 1 ( Hanoi )
- Two 、 Special solution example 2 ( The characteristic root is 1 The situation of )
One 、 Special solution example 1 ( Hanoi )
Hanoi problem :
- The recurrence equation is :
T
(
n
)
=
2
T
(
n
−
1
)
+
1
T(n) =2 T(n-1) + 1
T(n)=2T(n−1)+1
- initial value :
T
(
1
)
=
1
T(1) = 1
T(1)=1
Find the solution of the recursive equation ?
Solve its special solution first
1 . Special solution form :
On the left side of the above recursive equation is “ Linear homogeneous recurrence equation with constant coefficients ” form , Never mind ,
On the right side of the
1
1
1 Related to special solutions ,
1
1
1 by
n
n
n Of
0
0
0 Sub polynomial ,
Therefore, the special solution
H
∗
(
n
)
H^*(n)
H∗(n) It's also
n
n
n Of
0
0
0 Sub polynomial ;
2 . Write the special solution form :
Number of special solutions : be Number of special solutions yes
0
+
1
=
1
0 + 1 = 1
0+1=1 term ;
Understand each component : Each term is explained by constant multiply
n
n
n Power of power form ,
1
1
1 It's a constant Set to
P
1
P_1
P1 ,
1
1
1 individual
n
n
n Power of power , Power value
0
0
0 ,
Therefore, the form of the special solution is
T
∗
(
n
)
=
P
1
n
0
T^*(n) = P_1n^0
T∗(n)=P1n0 ,
It is reduced to :
T
∗
(
n
)
=
P
1
T^*(n) = P_1
T∗(n)=P1
3 . Put the special solution into the recursive equation :
Will explain
T
∗
(
n
)
=
P
1
T^*(n) = P_1
T∗(n)=P1 ,
Into the recursive equation
T
(
n
)
=
2
T
(
n
−
1
)
+
1
T(n) =2 T(n-1) + 1
T(n)=2T(n−1)+1 in ,
obtain :
P
1
=
2
P
1
+
1
P_1 = 2P_1 + 1
P1=2P1+1
The result of solving the equation :
P
1
=
−
1
P_1 = -1
P1=−1
The special solution is :
T
∗
(
n
)
=
−
1
T^*(n) = -1
T∗(n)=−1
The whole process of solving recursive equations : Solve the above Hanoi Tower Linear homogeneous recurrence equation with constant coefficients General solution of part ,
T
(
n
)
−
2
T
(
n
−
1
)
=
0
T(n) - 2 T(n-1) = 0
T(n)−2T(n−1)=0 ;
1 . Characteristic equation :
( 1 ) The standard form of recurrence equation : Write the recurrence equation Standard form , All items are to the left of the equal sign , On the right is
0
0
0 ;
T
(
n
)
−
2
T
(
n
−
1
)
=
0
T(n) - 2 T(n-1) = 0
T(n)−2T(n−1)=0
( 2 ) Number of terms of characteristic equation : determine Number of terms of characteristic equation , And The recurrence equation has the same number of terms ;
2
2
2 term ;
( 3 ) The characteristic equation is sub idempotent : The highest power is Number of terms of characteristic equation
−
1
-1
−1 , Lowest power
0
0
0 ;
Lowest power
0
0
0 , Highest power
1
1
1 ;
( 4 ) Write There is no coefficient The characteristic equation of ;
x
+
1
=
0
x + 1 = 0
x+1=0
( 5 ) The coefficients of the recursive equation will be deduced bit by bit Copy Into the characteristic equation ;
x
−
2
=
0
x - 2 = 0
x−2=0
2 . Solution characteristic root : take Characteristic equation Characteristic root Work it out ,
x
=
−
b
±
b
2
−
4
a
c
2
a
x = \cfrac{-b \pm \sqrt{b^2 - 4ac}}{2a}
x=2a−b±b2−4ac
Characteristic root
q
1
=
2
q_1=2
q1=2 ;
3 . Construct the general solution of recurrence equation :
( 1 ) No double root : structure
c
1
q
1
n
+
c
2
q
2
n
+
⋯
+
c
k
q
k
n
c_1q_1^n + c_2q_2^n + \cdots + c_kq_k^n
c1q1n+c2q2n+⋯+ckqkn Linear combination of forms , This linear combination is the of recursive equations general solution ;
The homogeneous partial general solution of the recurrence equation is :
T
(
n
)
‾
=
c
2
n
\overline{T(n)} = c2^n
T(n)=c2n
“ Linear Nonhomogeneous recurrence equation with constant coefficients ” The general solution is
T
(
n
)
=
T
(
n
)
‾
+
T
∗
(
n
)
T(n) = \overline{T(n)} + T^*(n)
T(n)=T(n)+T∗(n)
The special solution of the nonhomogeneous part is :
T
∗
(
n
)
=
−
1
T^*(n) = -1
T∗(n)=−1
Therefore, the general solution of Hanoi Tower recurrence equation is :
T
(
n
)
=
c
2
n
−
1
T(n) = c2^n - 1
T(n)=c2n−1
( 2 ) Double root : Refer to the following “ The general solution form under the double root is listed ” Content ;
4 . Find the constant in the general solution :
( 1 ) Substitute the initial values to obtain the equations : Substitute the initial value of the recursive equation into the general solution , obtain
k
k
k individual
k
k
k Finite element equations , adopt Solve the equations , obtain Constants in general solutions ;
Initial value
T
(
1
)
=
1
T(1) = 1
T(1)=1 Substitute the above general solution
T
(
n
)
=
c
2
n
−
1
T(n) = c2^n - 1
T(n)=c2n−1 , obtain
2
c
−
1
=
1
2c - 1 = 1
2c−1=1
constant
c
=
1
c = 1
c=1 ;
( 2 ) Substitute constants to obtain the general solution : Substitute constants into the general solution , You can get the final solution of the recursive equation ;
Will constant
c
=
1
c=1
c=1 Substitute into the general solution , The final result is the solution of the recursive equation :
T
(
n
)
=
2
n
−
1
T(n) = 2^n - 1
T(n)=2n−1
Two 、 Special solution example 2 ( The characteristic root is 1 The situation of )
The recurrence equation is :
H
(
n
)
−
H
(
n
−
1
)
=
7
n
H(n) - H(n-1) = 7n
H(n)−H(n−1)=7n , Find the general solution of the recursive equation ?
First find its homogeneous part
H
(
n
)
−
H
(
n
−
1
)
=
0
H(n) - H(n-1) = 0
H(n)−H(n−1)=0 A general understanding of ;
Write the characteristic equation :
x
−
1
=
0
x - 1 = 0
x−1=0 , The characteristic root is
q
=
1
q= 1
q=1 ;
Homogeneous partial general solution form :
H
(
n
)
‾
=
c
1
1
n
=
c
1
\overline{H(n)} =c_11^n = c_1
H(n)=c11n=c1
Find its special solution ( Failed attempts ) :
These are constant coefficients linear Nonhomogeneous equation , Then ask for it first Nonhomogeneous Part of it corresponds to Special solution ,
The right side is
n
n
n Of
1
1
1 Sub equation , Then the corresponding special solution is
H
∗
(
n
)
=
P
1
n
+
P
2
H^*(n) = P_1n + P_2
H∗(n)=P1n+P2 , The above special solution , Into the recursive equation ,
P
1
n
+
P
2
−
(
P
1
(
n
−
1
)
+
P
2
)
=
7
n
\ \ \ \ P_1n + P_2 - (P_1(n - 1) + P_2) =7n
P1n+P2−(P1(n−1)+P2)=7n , After simplification, it becomes :
P
1
n
+
P
2
−
P
1
n
+
P
1
−
P
2
=
7
n
\ \ \ \ P_1n + P_2 - P_1n + P_1 - P_2 = 7n
P1n+P2−P1n+P1−P2=7n
P
1
=
7
n
\ \ \ \ P_1 = 7n
P1=7n
At this time, the constant in the special solution cannot be solved
P
1
,
P
2
P_1, P_2
P1,P2 , Therefore, the special solution cannot be set as
n
n
n Of
1
1
1 Sub equation ,
The reason for this problem is , Homogeneous part , The characteristic equation is
x
−
1
=
0
x-1 = 0
x−1=0 , The corresponding characteristic root is
1
1
1 ,
The characteristic root is
1
1
1 when , The highest term of the polynomial will cancel , The constant term will also be offset ;
Seeking special solution , take
n
n
n To the power of
1
1
1 :
The power of increase is Characteristic root
1
1
1 The repeatability of , If the repetition is
2
2
2 , You need to improve
2
2
2 The next power ;
In order to solve the above problems , Here we need to
n
n
n To the power of
1
1
1 , Let the first power term in the form of special solution , Set to square , The constant term is not set , Even if it is set, it will offset , Cannot find the value of the constant term ;
Set the special solution to
n
n
n Of
2
2
2 Sub equation ,
The special solution is in the form of
H
∗
(
n
)
=
P
1
n
2
+
P
2
n
H^*(n) = P_1n^2 + P_2n
H∗(n)=P1n2+P2n ;
Put the special solution into the recursive equation :
P
1
n
2
+
P
2
n
−
(
P
1
(
n
−
1
)
2
+
P
2
(
n
−
1
)
)
=
7
n
P_1n^2 + P_2n - ( P_1(n-1)^2 + P_2(n-1) )=7n
P1n2+P2n−(P1(n−1)2+P2(n−1))=7n
P
1
n
2
+
P
2
n
−
(
P
1
(
n
2
−
2
n
+
1
)
+
P
2
(
n
−
1
)
)
=
7
n
P_1n^2 + P_2n - ( P_1(n^2 -2n + 1) + P_2(n-1) )=7n
P1n2+P2n−(P1(n2−2n+1)+P2(n−1))=7n
P
1
n
2
+
P
2
n
−
P
1
n
2
+
2
P
1
n
−
P
1
−
P
2
n
+
P
2
=
7
n
P_1n^2 + P_2n - P_1n^2 + 2P_1n - P_1 - P_2n + P_2=7n
P1n2+P2n−P1n2+2P1n−P1−P2n+P2=7n
2
P
1
n
−
P
1
+
P
2
=
7
n
2P_1n - P_1 + P_2=7n
2P1n−P1+P2=7n
analysis
n
n
n Write the system of equations by the power of :
The left and right sides are equal , here according to
n
n
n The coefficient before the power of , Write the equations ;
analysis
n
n
n Coefficient to the power of :
n
2
n^2
n2 Coefficient analysis : There's no on the right
n
2
n^2
n2 , So on the left
n
2
n^2
n2 The coefficient before the term is
0
0
0 ; Nor on the left
n
2
n^2
n2 term , Unable to extract equation ;
n
1
n^1
n1 Coefficient analysis : The right side is
7
n
7n
7n , therefore
n
n
n The coefficient before is
7
7
7 ; Expand the left side ,
n
n
n The coefficient before is
2
P
1
2P_1
2P1 ;
2
P
1
n
=
7
n
2P_1n = 7n
2P1n=7n
n
0
n^0
n0 Coefficient analysis : The right side is
0
0
0 ; Expand the left side ,
n
0
n^0
n0 The coefficient before is
P
2
−
P
1
P_2-P_1
P2−P1 ;
P
2
−
P
1
=
0
P_2-P_1 = 0
P2−P1=0
Finally, we get the equations :
{
2
P
1
=
7
−
P
1
+
P
2
=
0
\begin{cases} 2P_1 = 7 \\\\ -P_1 + P_2 = 0 \end{cases}
⎩⎪⎨⎪⎧2P1=7−P1+P2=0
Solve the above equations , Get the results :
{
P
1
=
7
2
P
2
=
7
2
\begin{cases} P_1 = \cfrac{7}{2} \\\\ P_2 = \cfrac{7}{2} \end{cases}
⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧P1=27P2=27
The special solution is :
H
∗
(
n
)
=
7
2
n
2
+
7
2
n
H^*(n) = \cfrac{7}{2} n^2 + \cfrac{7}{2}n
H∗(n)=27n2+27n
Homogeneous partial general solution form :
H
(
n
)
‾
=
c
1
\overline{H(n)} = c_1
H(n)=c1
The final general solution is :
H
(
n
)
=
H
(
n
)
‾
+
H
∗
(
n
)
=
c
1
+
7
2
n
2
+
7
2
n
H(n) = \overline{H(n)} + H^*(n) = c_1 +\cfrac{7}{2} n^2 + \cfrac{7}{2}n
H(n)=H(n)+H∗(n)=c1+27n2+27n
边栏推荐
- C language string inversion
- Kotlin learning quick start (7) -- wonderful use of expansion
- Electronic Science and technology 20th autumn "Microcomputer Principle and application" online assignment 2 [standard answer]
- 建立自己的网站(23)
- 【JokerのZYNQ7020】DDS_ Compiler。
- vs code 插件 koroFileHeader
- A day's work list of an ordinary programmer
- An example of HP array card troubleshooting
- Leetcode13. Roman numeral to integer (three solutions)
- Kotlin learning quick start (7) -- wonderful use of expansion
猜你喜欢

手把手带你入门 API 开发
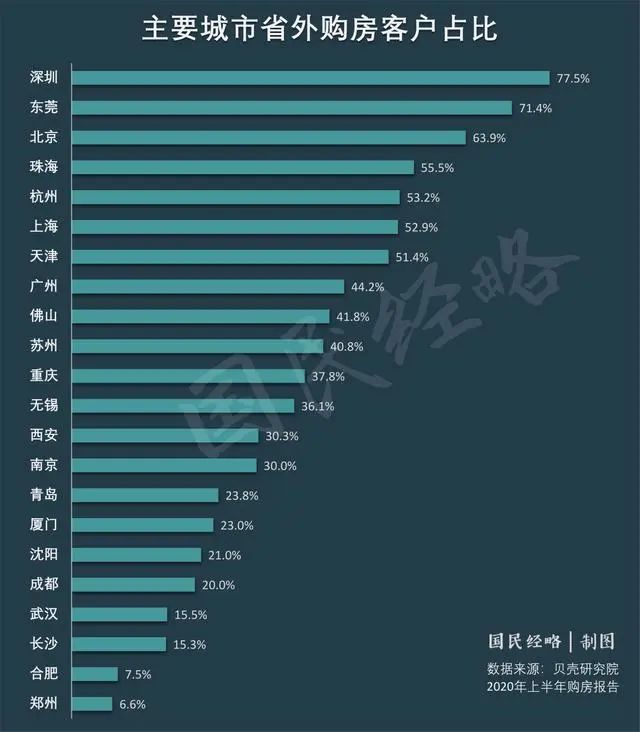
Great changes! National housing prices fell below the 10000 yuan mark
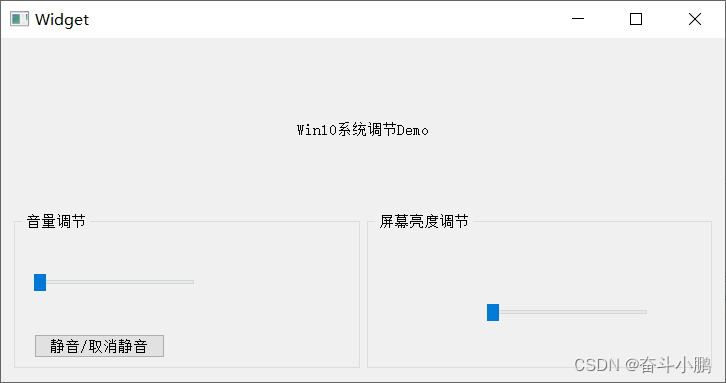
Qt调节Win屏幕亮度和声音大小
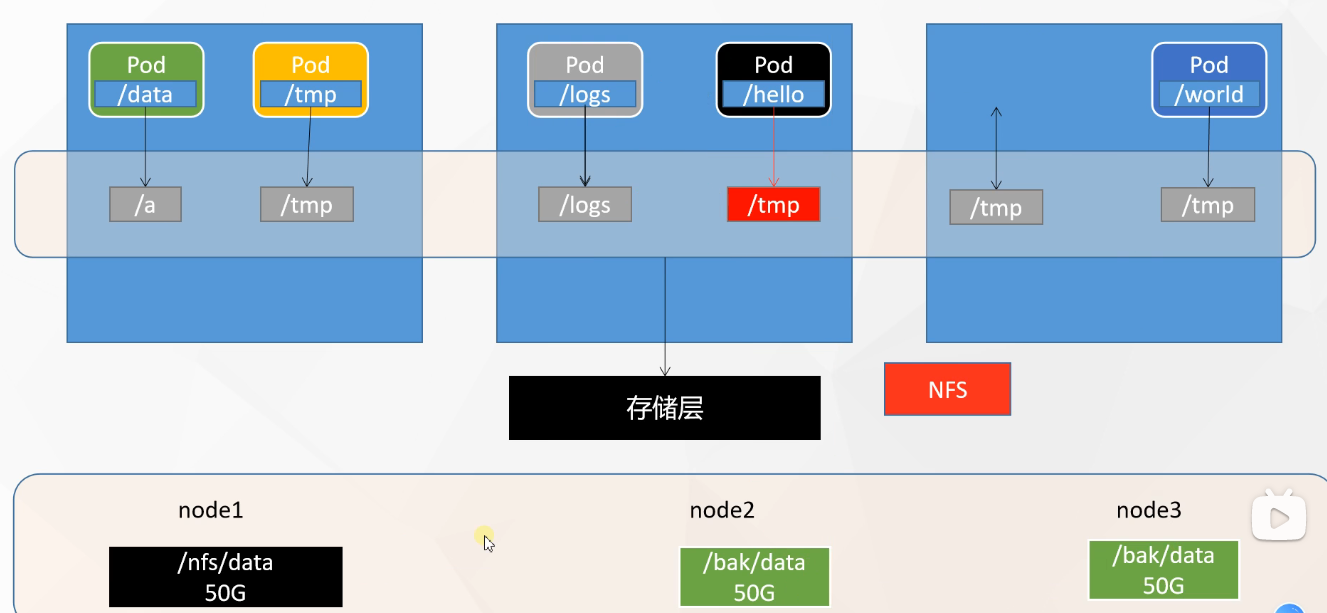
kubernetes资源对象介绍及常用命令(五)-(NFS&PV&PVC)

【JokerのZYNQ7020】DDS_ Compiler。
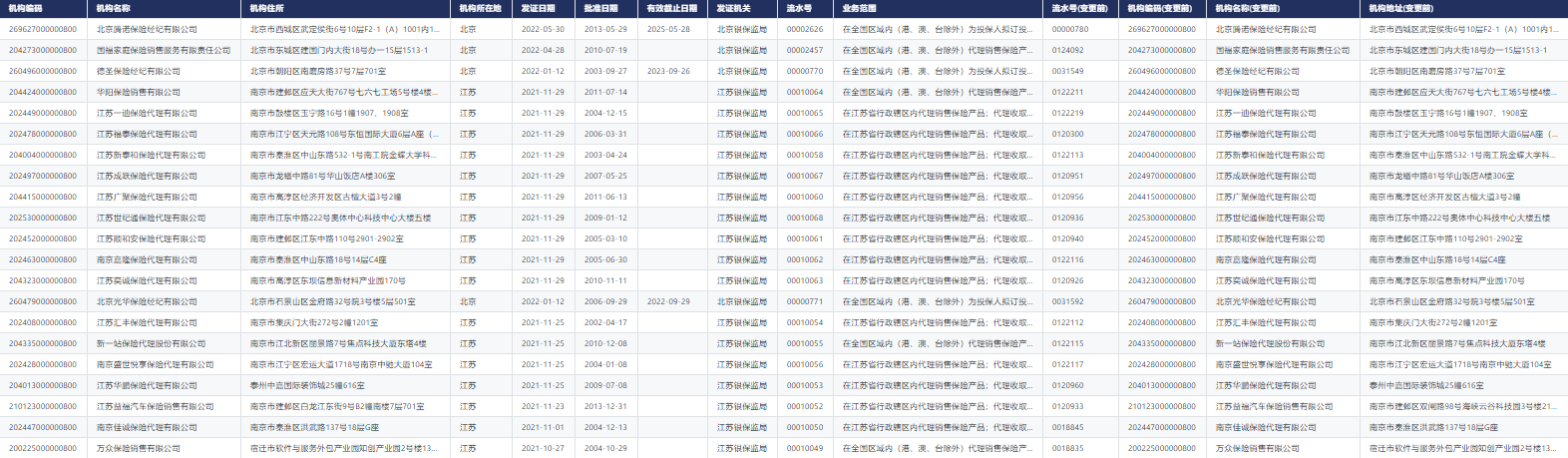
Free data | new library online | cnopendata complete data of China's insurance intermediary outlets

線程池:業務代碼最常用也最容易犯錯的組件

New features of C 10

Build your own website (23)

人生还在迷茫?也许这些订阅号里有你需要的答案!
随机推荐
One brush 145 force deduction hot question-2 sum of two numbers (m)
[combinatorics] recursive equation (constant coefficient linear homogeneous recursive equation | constant coefficient, linear, homogeneous concept description | constant coefficient linear homogeneous
University of Electronic Science and technology, accounting computerization, spring 20 final exam [standard answer]
Free data | new library online | cnopendata complete data of China's insurance intermediary outlets
免费数据 | 新库上线 | CnOpenData中国保险中介机构网点全集数据
大变局!全国房价,跌破万元大关
29: Chapter 3: develop Passport Service: 12: develop [obtain user account information, interface]; (use VO class to package the found data to meet the requirements of the interface for the returned da
【RT-Thread】nxp rt10xx 设备驱动框架之--Pin搭建和使用
PHP online confusion encryption tutorial sharing + basically no solution
RF analyze demo build step by step
Luogu: p2685 [tjoi2012] Bridge
Installation and configuration of network hard disk NFS
Take you to API development by hand
How do large consumer enterprises make digital transformation?
绝对定位时元素水平垂直居中
visual studio “通常每个套接字地址(协议/网络地址/端口)只允许使用一次“
What is your income level in the country?
An example of HP array card troubleshooting
Thread pool: the most common and error prone component of business code
BYD and great wall hybrid market "get together" again