当前位置:网站首页>【AtCoder2376】Black and White Tree(博弈)
【AtCoder2376】Black and White Tree(博弈)
2022-06-11 07:23:00 【CaptainHarryChen】
题意
A和B轮流给树上的结点染色,A每次选择没染过的点染成白色,B每次选择没染过的点染成黑色,最后若所有白色都与黑色相邻,则B胜,否则A胜。双方以最优策略,求A胜还是B胜。
题解
A首先选择叶子结点的父亲u,则B只能选择叶子结点(否则叶子节点染白后,永远不可能与黑色相邻),所以,如果存在u有两个以上叶子结点,则A胜;
然后删去u,则u的父亲v,如果v没有了子节点,v就成为新的叶子结点,A可继续先前的操作,B永远处于被动当中。
当遇到一下两种情况时,A必胜
- 当前结点u含有两个或以上叶子结点
- 若u为根,且u的所有子节点都被染为白色(这时把自己染为白色即可)
dfs处理一边即可。
代码
#include<cstdio> #include<cstring> #include<vector> #include<algorithm> using namespace std; const int MAXN=100005; int N; vector<int> adj[MAXN]; int col[MAXN]; bool dfs(int u,int f) {
if(adj[u].size()==1U) {
col[u]=0;//标记为叶子结点 return false; } int cnt[2]={
0}; for(int i=0;i<(int)adj[u].size();i++) {
int v=adj[u][i]; if(v==f) continue; if(dfs(v,u)) return true; cnt[col[v]]++; } if(cnt[0]>=2) return true;//叶子结点大于等于2 if(f==0&&(int)adj[u].size()==cnt[1]) return true;//当前u为根,u的所有子节点均为白色 if(cnt[0]) col[u]=1;//如果有叶子结点,这个点染白 else col[u]=0;//这个点的子节点全部被染白(被删去),当前u变为叶子结点 return false; } int main() {
scanf("%d",&N); for(int i=1;i<N;i++) {
int u,v; scanf("%d%d",&u,&v); adj[u].push_back(v); adj[v].push_back(u); } if(N==2) puts("Second"); else {
bool ans; for(int i=1;i<=N;i++) if(adj[i].size()>1U) {
ans=dfs(i,0); break; } puts(ans?"First":"Second"); } return 0; } 边栏推荐
- Sqlzoo question brushing record-3
- Crmeb/v4.4 Standard Version open version mall source code applet official account h5+app mall source code
- 教育专家王中泽老师多年经验分享:家庭教育不是附庸品
- Pointer to a two-dimensional array
- Decimal to binary
- What is the lifecycle of automated testing?
- [STL source code analysis] summary notes (5): a good helper for understanding iterators --list
- SQLZOO刷题记录-3
- Atomicinteger atomic operation class
- Summary of written test questions of shopee 2021 autumn recruitment
猜你喜欢
![[并发进阶]——线程池总结](/img/69/dc8146dafc30f8a8efa012b67aa05c.png)
[并发进阶]——线程池总结

Seata的几种事务模式
![Error occurred in pycharm DeprecatedEnv: Env FrozenLake-v0 not found (valid versions include [‘FrozenLake-v1‘])](/img/1c/4013479ce1fc5b0ff2ebeb754f05a9.png)
Error occurred in pycharm DeprecatedEnv: Env FrozenLake-v0 not found (valid versions include [‘FrozenLake-v1‘])

Leetcode-104. Maximum Depth of Binary Tree

webserver

Niuke wrong question 3.1

Senior openstacker - Bloomberg, vexxhost upgraded to gold member of openinfra Foundation

2022 low voltage electrician operation certificate test question simulation test platform operation
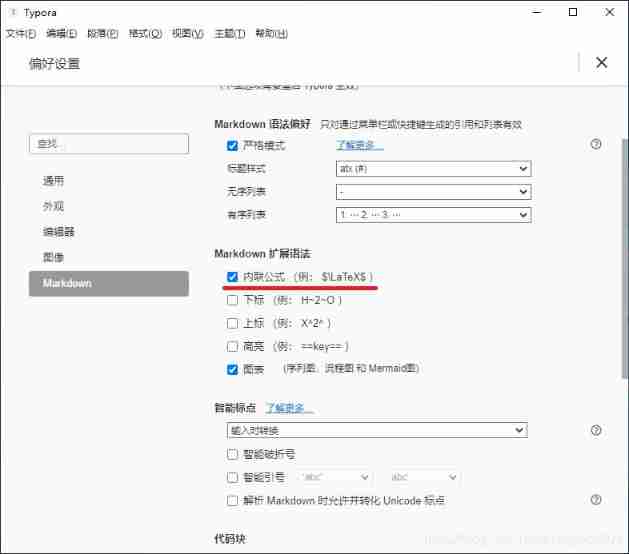
Typora set markdown syntax inline mode

JVM learning record (VII) -- class loading process and parental delegation model
随机推荐
@JsonProperty注解
Crmeb/v4.4 Standard Version open version mall source code applet official account h5+app mall source code
【CF#262 (Div. 2)】 A. Vasya and Socks
2022低压电工考题及在线模拟考试
Matplotlib, set coordinate scale size, font / set legend size and font / set vertical and horizontal coordinate name, font and size
[STL source code analysis] summary notes (9): set/multiset and map/multimap
MS office level II wrong question record [8]
Compound RateModel合約解析
Summary of written test questions of shopee 2021 autumn recruitment
QT 基于QScrollArea的界面嵌套移动
The maximum number of divisors of numbers in the int range is 1536
Android和iOS逆向分析/安全检测/渗透测试框架
1190. invert the substring between each pair of parentheses
P3327 [sdoi2015] approximate sum (Mobius inversion + formula)
多线程复习总结之解析Volatile关键字
1、 Sqlserver2008 installation (with password), database creation, C form project test
If you want to save an IP address, what data type is better? 99% of people will answer wrong!
MS office level II wrong question record [7]
【Oracle 数据库】奶妈式教程day04 排序查询
一、SQLServer2008安装(带密码)、创建数据库、C#窗体项目测试