当前位置:网站首页>[acnoi2022] not a structure, more like a structure
[acnoi2022] not a structure, more like a structure
2022-06-24 08:26:00 【OneInDark】
subject
Title Description
to n n n spot m m m Edge undirected graph . Initially all edges are DDG \textsf{DDG} DDG Guard and cannot pass . however , remember S i S_i Si The connected block formed for the passable edges contains i i i the , if ∑ x ∈ S u a x + ∑ y ∈ S v a y ⩾ e a , b \sum_{x\in S_u}a_x+\sum_{y\in S_v}a_y\geqslant e_{a,b} ∑x∈Suax+∑y∈Svay⩾ea,b And v ∉ S u v\notin S_u v∈/Su, be * u , v * \langle u,v\rangle *u,v* The black bridge can be built on ( Would not have been DDG \textsf{DDG} DDG The intrusion of ) And so it can be passed ! Of course S S S Will also change accordingly .
In all scenarios , Under the premise that the total number of black bridges built is the largest , The construction sequence with the smallest dictionary order .
Data range and tips
n ⩽ 1 0 5 n\leqslant 10^5 n⩽105, Border right e u , v ⩽ 1 0 6 e_{u,v}\leqslant 10^6 eu,v⩽106, Point right a i ∈ [ 0 , 1 0 6 ] a_i\in[0,10^6] ai∈[0,106] .
Ideas
Save the flow : There is no reference value . Just memorize it as a conclusion .
First reaction : Maintenance required O ( deg ) \mathcal O(\deg) O(deg) Information about . Heuristic merging ? Divide and conquer big and small points ? Didn't get through .
An obscure condition : The judgment condition of an edge is only related to the change of two values . So there was a way that could not be thought of by ordinary people like me : For each edge , Suppose that sum ( S u ) + sum ( S v ) \text{sum}(S_u)+\text{sum}(S_v) sum(Su)+sum(Sv) still need sth. δ \delta δ Increase of . be sum ( S u ) \text{sum}(S_u) sum(Su) and sum ( S v ) \text{sum}(S_v) sum(Sv) At least one of them has ⌈ δ 2 ⌉ \lceil{\delta\over 2}\rceil ⌈2δ⌉ Increase of .
So the t a g \rm tag tag In the play , Check when triggered , Merging connected blocks is heuristic merging . One edge is only checked log e \log e loge Time , Therefore, the total complexity is low O [ m log m ( log m + log e ) ] \mathcal O[m\log m(\log m+\log e)] O[mlogm(logm+loge)] or O ( m log m log e ) \mathcal O(m\log m\log e) O(mlogmloge) .
Code
#include <cstdio>
#include <algorithm> // Almighty XJX yyds!!
#include <cstring> // oracle: ZXY yydBUS!!!
#include <cctype> // Huge Egg Dog ate me!!!
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <functional>
#include <utility>
#include <queue>
using namespace __gnu_pbds;
using llong = long long;
# define rep(i,a,b) for(int i=(a); i<=(b); ++i)
# define drep(i,a,b) for(int i=(a); i>=(b); --i)
# define rep0(i,a,b) for(int i=(a); i!=(b); ++i)
inline int readint(){
int a = 0, c = getchar(), f = 1;
for(; !isdigit(c); c=getchar()) if(c == '-') f = -f;
for(; isdigit(c); c=getchar()) a = a*10+(c^48);
return a*f;
}
const int MAXN = 100000;
using PII = std::pair<int,int>;
tree<PII,null_type,std::less<PII>,splay_tree_tag> tre[MAXN];
int val[MAXN], fa[MAXN];
inline int findSet(int a){
if(fa[a] == a) return a;
return fa[a] = findSet(fa[a]);
}
std::priority_queue<int> todo;
int cost[MAXN<<1], ep[MAXN<<1][2];
std::queue<int> ans;
int main(){
int n = readint(), m = readint();
rep0(i,0,n) val[i] = readint(), fa[i] = i;
for(int i=0,a,b; i!=m; ++i){
a = ep[i][0] = readint()-1;
b = ep[i][1] = readint()-1;
cost[i] = readint();
if(val[a]+val[b] >= cost[i]) todo.push(-i);
else{
// half to check
tre[a].insert(PII{
(cost[i]+1+val[a]-val[b])>>1, i});
tre[b].insert(PII{
(cost[i]+1-val[a]+val[b])>>1, i});
}
}
while(!todo.empty()){
int x = -todo.top(); todo.pop();
if(findSet(ep[x][0]) == findSet(ep[x][1])) continue;
int faa = findSet(ep[x][0]), fab = findSet(ep[x][1]);
if(tre[fab].size() > tre[faa].size()) tre[faa].swap(tre[fab]);
for(const PII &v : tre[fab]) tre[faa].insert(v);
val[faa] += val[fab], ans.push(x), fa[fab] = faa;
while(!tre[faa].empty() && tre[faa].begin()->first <= val[faa]){
x = tre[faa].begin()->second;
tre[faa].erase(tre[faa].begin());
if(findSet(ep[x][0]) == findSet(ep[x][1])) continue;
int l = findSet(ep[x][0]), r = findSet(ep[x][1]);
if(val[l]+val[r] >= cost[x]) todo.push(-x); // available
else{
// still cut in half
tre[l].insert(PII{
(cost[x]+1+val[l]-val[r])>>1, x});
tre[r].insert(PII{
(cost[x]+1-val[l]+val[r])>>1, x});
}
}
}
printf("%d\n",int(ans.size()));
for(; !ans.empty(); ans.pop())
printf("%d ",ans.front()+1);
putchar('\n');
return 0;
}
边栏推荐
- 蓝桥杯_N 皇后问题
- etcd备份恢复原理详解及踩坑实录
- List of Li Bai's 20 most classic poems
- Dart development server, do I have a fever?
- Swift foundation features unique to swift
- 新技术实战,一步步用Activity Results API封装权限申请库
- Blue Bridge Cup_ Queen n problem
- [ACNOI2022]做过也不会
- 487. number of maximum consecutive 1 II ●●
- WCF TCP protocol transmission
猜你喜欢
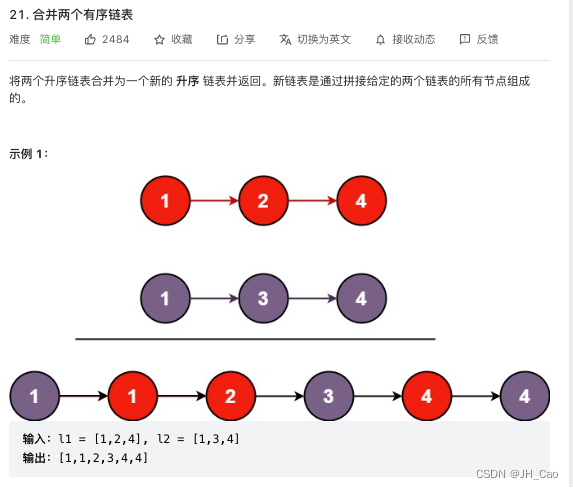
12--合并两个有序链表

A preliminary study of IO model

2021-03-04 COMP9021第六节课笔记

Pagoda panel installation php7.2 installation phalcon3.3.2

2021-03-04 comp9021 class 6 notes

Permission model DAC ACL RBAC ABAC

小样本故障诊断 - 注意力机制代码 - BiGRU代码解析实现
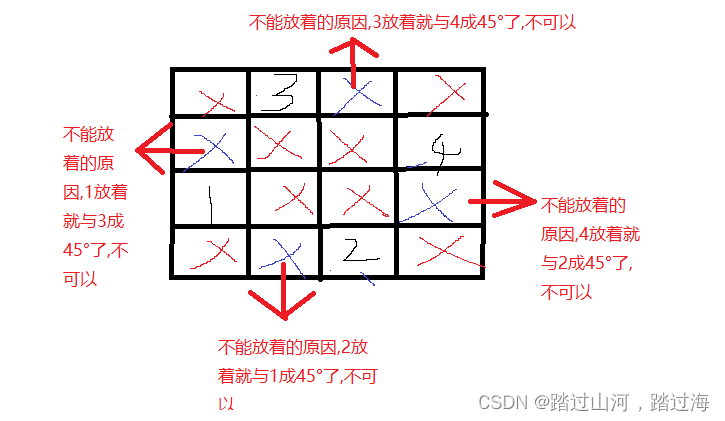
蓝桥杯_N 皇后问题

The article takes you to understand the security of Windows operating system and protect your computer from infringement

Live broadcast review | detailed explanation of koordinator architecture of cloud native hybrid system (complete ppt attached)
随机推荐
问题4 — DatePicker日期选择器,2个日期选择器(开始、结束日期)的禁用
51单片机_外部中断 与 定时/计数器中断
The article takes you to understand the security of Windows operating system and protect your computer from infringement
Analysis of abnormal problems in domain name resolution in kubernetes
487. number of maximum consecutive 1 II ●●
软件过程与项目管理期末复习与重点
Search and recommend those things
LINQ query (2)
[ACNOI2022]做过也不会
[ACNOI2022]不是构造,胜似构造
5分钟,客服聊天处理技巧,炉火纯青
基金的募集,交易与登记
Model effect optimization, try a variety of cross validation methods (system operation)
Application of JDBC in performance test
2021-03-09 comp9021 class 7 Notes
Question 3 - MessageBox pop-up box, modify the default background color
1279_ Vsock installation failure resolution when VMware player installs VMware Tools
Permission model DAC ACL RBAC ABAC
你还只知道测试金字塔?
The JS macro of WPS implements the separation method of picture text in the same paragraph