当前位置:网站首页>[R language data science]: cross validation and looking back
[R language data science]: cross validation and looking back
2022-07-04 14:03:00 【JOJO's data analysis Adventure】
【R Language data science 】: Cross verify and look back
- Personal home page :JoJo Data analysis adventure
- Personal introduction : I'm reading statistics in my senior year , At present, Baoyan has reached statistical top3 Colleges and universities continue to study for Postgraduates in Statistics
- If it helps you , welcome
Focus on、give the thumbs-up、Collection、subscribespecial column- This article is included in 【R Language data science 】 This series mainly introduces R The applications of language in the field of data science include :
R Fundamentals of language programming 、R Language visualization 、R Language for data manipulation 、R Modeling language 、R Language machine learning algorithm implementation 、R Language statistical theory and method . This series will continue to be completed , Please pay more attention, praise and support , Learning together ~, Try to keep updating every week , Welcome to subscribe to exchange study !

List of articles
Preface
Cross validation can be used to calculate the test errors associated with a given statistical learning method , To evaluate its performance , Or choose the appropriate level of flexibility , Make a super parameter adjustment . The process of evaluating model performance is called model evaluation , The process of model evaluation to select the appropriate level of flexibility for the model is called model selection . In the last chapter , We discussed the training set and the test set . We tend to pay more attention to the error of the model in the test set ( Test error ). Test error is the average error of statistical learning method in predicting new data sets . Under a given data set , If the test error of a specific statistical learning method is very low , So the effect of this model is good . by comparison , Training error is easy to get and control . Training error is usually very different from test error , Often the training error is greater than the test error . In the absence of a test set that can be used to directly estimate the test error , A variety of mathematical techniques can be used to adjust training errors , To estimate the test error . Then we'll go into detail . In this chapter , We considered the method of dividing the data set . We need to partition the data set : Training set 、 Verification set 、 Test set . Sometimes you put validation sets and test sets together ) Common cross validation methods are 2 individual :
- K Crossover verification
- Leave one method for cross validation
1 K Crossover verification
Our first discussion is K Crossover verification . Generally speaking , Machine learning challenges begin with a Data sets ( Blue in the picture below ). We need to use this data set to build an algorithm , The algorithm will eventually be used for completely independent Data sets ( yellow ).
But in reality , We don't know the Yellow data set .
therefore , To simulate this , We split a part of the data set and pretend that it is an independent data set , As shown in the figure below, we divide the data set into Training set ( Blue ) and Test set ( Red ). We will specialize in Train our algorithm on the training set , And use the test set for evaluation purposes only .
We usually try to select a small number of data sets as test sets , So that we can train with as much data as possible . however , We also hope that the test set is large enough , In this way, we can obtain a stable loss estimate without fitting the unrealistic number of models . The typical choice is to use 20%-30% As a test set . Of course, there are tens of millions of data now , A smaller proportion may be used .
![[ Failed to transfer the external chain picture , The origin station may have anti-theft chain mechanism , It is suggested to save the pictures and upload them directly (img-pdGV1xio-1656858582711)(https://s2.loli.net/2022/07/03/PfUQqM7yVFx9sGL.png)]](/img/85/03960fd63da4798abd2a6f0e74d3fc.png)
Now here is a new question , Because for most machine learning algorithms , We need to choose the super parameter . for example KNN In the algorithm k. These parameters are not trained by the model , That is, we often say the super parameter of the parameter adjustment part , We need to optimize the algorithm parameters without using our test set , We know that if we optimize and evaluate on the same data set , It's easy to over fit (Overfitting). This is where cross validation is most useful . For each set of algorithm parameters , We need a MSE The estimate of , Then we will choose to have the smallest MSE The super parameter of λ \lambda λ.
M S E ( λ ) = 1 k ∑ i = 1 k 1 n ∑ i = 1 n ( y i ^ ( λ ) − y i ) 2 MSE(\lambda) = \frac{1}{k}\sum_{i=1}^{k}\frac{1}{n}\sum_{i=1}^{n}(\hat{y_i}(\lambda)-y_i)^2 MSE(λ)=k1i=1∑kn1i=1∑n(yi^(λ)−yi)2
among k Indicates the number of cross validation ,n Represents the sample size
Now we can further divide the training set into training set and verification set , We fit the model on the training set , Then calculate MSE, As shown in the figure below
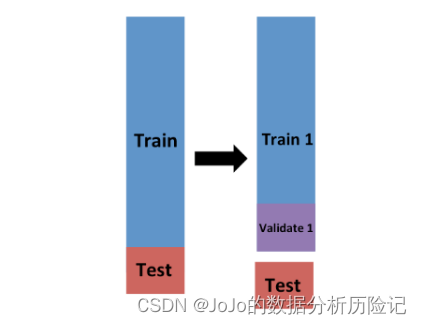
Calculation
Validate1Upper MSE:
M S E ( λ ) = 1 m ∑ i = 1 m ( y i ^ ( λ ) − y i ) 2 MSE(\lambda) = \frac{1}{m}\sum_{i=1}^{m}(\hat{y_i}(\lambda)-y_i)^2 MSE(λ)=m1i=1∑m(yi^(λ)−yi)2
among m Represents the samples on each validation set
Be careful : As mentioned above, we only calculated the MSE, To improve generalization , We set it up k Verification sets , First of all, the overall training set is divided into k A Disjoint Set , Select one of the sets as the validation set each time ,k-1 As a training set , And then we get M S E 1 , . . . , M S E k MSE_1,...,MSE_k MSE1,...,MSEk, Then calculate their average :
M S E ( λ ) = 1 k ∑ i = 1 k M S E i ( λ ) MSE(\lambda) = \frac{1}{k}\sum_{i=1}^{k}MSE_i(\lambda) MSE(λ)=k1i=1∑kMSEi(λ)
Our goal is to make this average MSE Minimum

Now we have described how to use cross validation to optimize parameters to select models . however , We must now take into account the fact that the above optimization occurs on the training data , Therefore, we need to estimate the final algorithm based on the data not used for optimal selection . This is where we use early separated test sets :
![[ Failed to transfer the external chain picture , The origin station may have anti-theft chain mechanism , It is suggested to save the pictures and upload them directly (img-AUyEOAWo-1656858582712#pic_center)(https://s2.loli.net/2022/07/03/aehYS8XZutK4W7r.png)]](/img/ea/4a523dec9f706842318c56f3259c33.png)
We can cross verify again :
![[ Failed to transfer the external chain picture , The origin station may have anti-theft chain mechanism , It is suggested to save the pictures and upload them directly (img-Mj0Noh3S-1656858582712)(https://s2.loli.net/2022/07/03/Krce4QBj6AqxW5w.png)]](/img/ba/6eba2e176f43213bced56d4828fb3d.png)
After having the test set , We can evaluate this test set .K The idea of fold cross validation is to divide the data set into K Group . The first group is the test set , The rest k-1 Group as training set . M S E 1 MSE_1 MSE1 It can be seen as the first training , The average error of the test group . repeat k Time , We can get k- Test error of fold cross validation :
C V ( k ) = 1 k ∑ i = 1 k M S E i . CV_{(k)}=\frac{1}{k}\sum_{i=1}^{k}MSE_i. CV(k)=k1i=1∑kMSEi.
And get the final estimate of our expected loss . however , Please note that , This means that our entire calculation time is multiplied by k. Because we are performing many complex calculations . therefore , We need to find ways to reduce time . For the final assessment , We usually use only one test set .
Once we have determined the final model through cross validation , We can re fit the model on the whole data set , Without changing the optimization parameters . In this way, we have more training data . This is effective , Especially when the amount of data is small .
Now we need to consider how to choose K? After a lot of attempts and experience , At present, the commonly used choice is
10or5, This is also r and python Default discount
2 K-fold Cross validation code implementation
cv.glm() function Can achieve k Crossover verification , Let's use k=10, It's also one we often use k value . Let's reset the random seed number , stay Auto Data set fitting model , Fitting polynomial regression of one degree to ten degrees respectively
# 7 It's my lucky number , I just set it up
library(ISLr2)
library(boot)
set.seed(7)
# Initialize the vector to save 10 Results of fold cross validation
cv_error_10 <- rep(0,10)
for (i in 1:10){
glm.fit <- glm(mpg~poly(horsepower,i), data = Auto)
cv_error_10[i] <- cv.glm(Auto,glm.fit,K = 10)$delta[1]
}
cv_error_10
Get the error of each model :
- 24.1463716629577
- 19.3130825829741
- 19.434897545051
- 19.5493689322887
- 19.0736379228708
- 18.7058531603005
- 19.2522869995751
- 18.8552270777634
- 18.9304332711781
- 20.4425474405408
Visualize the results
x <- seq(1,10)
library(ggplot2)
kcv <- data.frame(x,cv=cv_error_10)
ggplot(kcv, aes(x, cv)) +geom_point() + geom_line(lwd=1,col='blue')
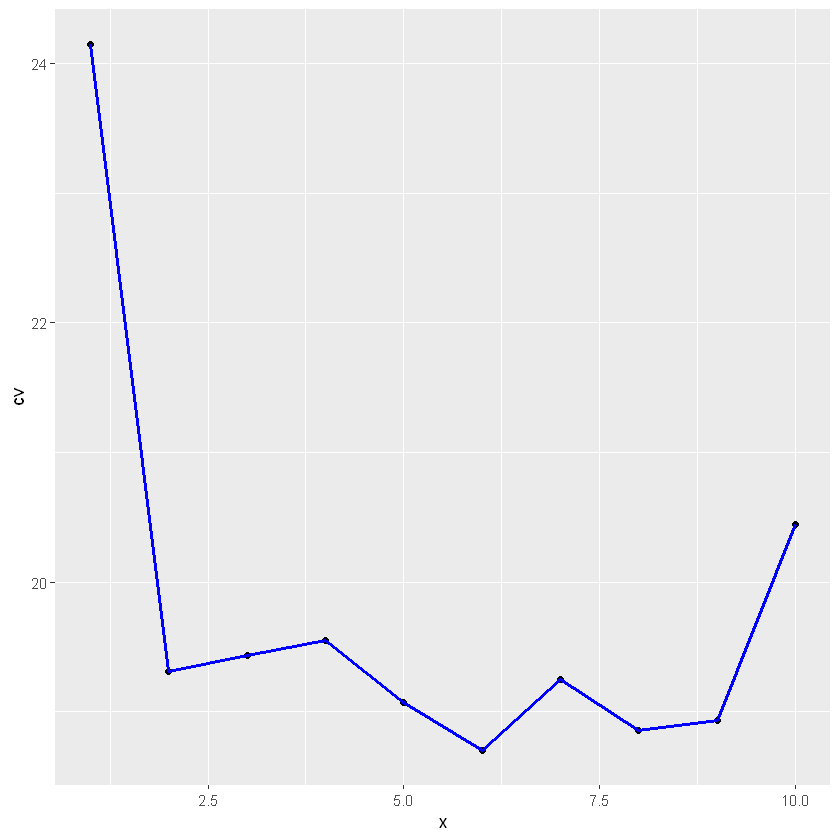
Sure See 2 The accuracy of secondary fitting is improved , It can be seen that the accuracy of quadratic fitting is improved higher , Higher fitting does not significantly improve the accuracy of the model
3. Leave one method for cross validation (LOOCV)
Leaving one method for cross validation can be seen as a transformation of the above methods . Similarly, the data set is divided into two parts , Part as validation set , Part of it is a training set , The difference is , We do not choose the same sample size as the validation set here , And just choose a sample ( x 1 , y 1 ) (x_1,y_1) (x1,y1) As validation set . The rest n-1 Samples as training set : ( x 2 , y 2 ) , . . . , ( x n , y n ) {(x_2,y_2),...,(x_n,y_n)} (x2,y2),...,(xn,yn), Fitting model
We are equivalent to doing n Second model training , And then n The average test error of sub fitting is used to estimate the test error of a specific model . The test error obtained from the first training is : M S E 1 = ( y 1 − y ^ 1 ) 2 MSE_1=(y_1-\hat{y}_1)^2 MSE1=(y1−y^1)2. repeat n Time to get : M S E 2 , . . . , M S E n MSE_2,...,MSE_n MSE2,...,MSEn. Finally, we take the average value to LOOCV Estimated test MSE:
C V ( n ) = 1 n ∑ i = 1 n M S E i . CV_{(n)}=\frac{1}{n}\sum_{i=1}^{n}MSE_i. CV(n)=n1i=1∑nMSEi.
LOOCV There are mainly the following points advantage :
- 1. Less deviation , Because we use more data sets for training
- 2. Will not be affected by the randomness of sampling .
Leaving one method for cross validation is a very general Methods , For example, in logistic regression perhaps naive bayes Can be used in .
One disadvantage of the cross validation with the leave one method is that it requires a large amount of calculation , Because we have to fit n Sub model . In some problems now , The amount of data is almost always G Even larger , At this time, fitting the model will take too much time . Compared with k Folding cross validation is an obvious disadvantage .
4. Leave one way to cross verify the code implementation
loocv The results can be used directly glm() Functions and cv.glm() Function to get . We used glm() The function fits logistic Return to , Remember we used family Parameters =binomal, If we don't specify family value , The default is linear regression , and lm() The function is the same . Let's use glm() and cv.glm() To achieve LOOCV, First, import. boot package
library(boot)
glm.fit <- glm(mpg~horsepower, data = Auto)
cv.err <- cv.glm(Auto,glm.fit)
cv.err$delta
- 24.2315135179292
- 24.2311440937562
You can see the above two MSE Almost the same , because LOOCV The results of almost every training are the same . Be careful , In the use of cv.glm() when , There is no need to specify train, It's automatic LOOCV The process . Now let's look at the polynomial results to different powers
cv.error <- rep(0,10)
for (i in 1:10) {
glm.fit <- glm(mpg~poly(horsepower,i),data= Auto)
cv.error[i] <- cv.glm(Auto, glm.fit)$delta[1]
}
cv.error
- 24.2315135179293
- 19.2482131244897
- 19.334984064029
- 19.4244303104303
- 19.0332138547041
- 18.9786436582254
- 18.8330450653183
- 18.9611507120531
- 19.0686299814599
- 19.490932299334
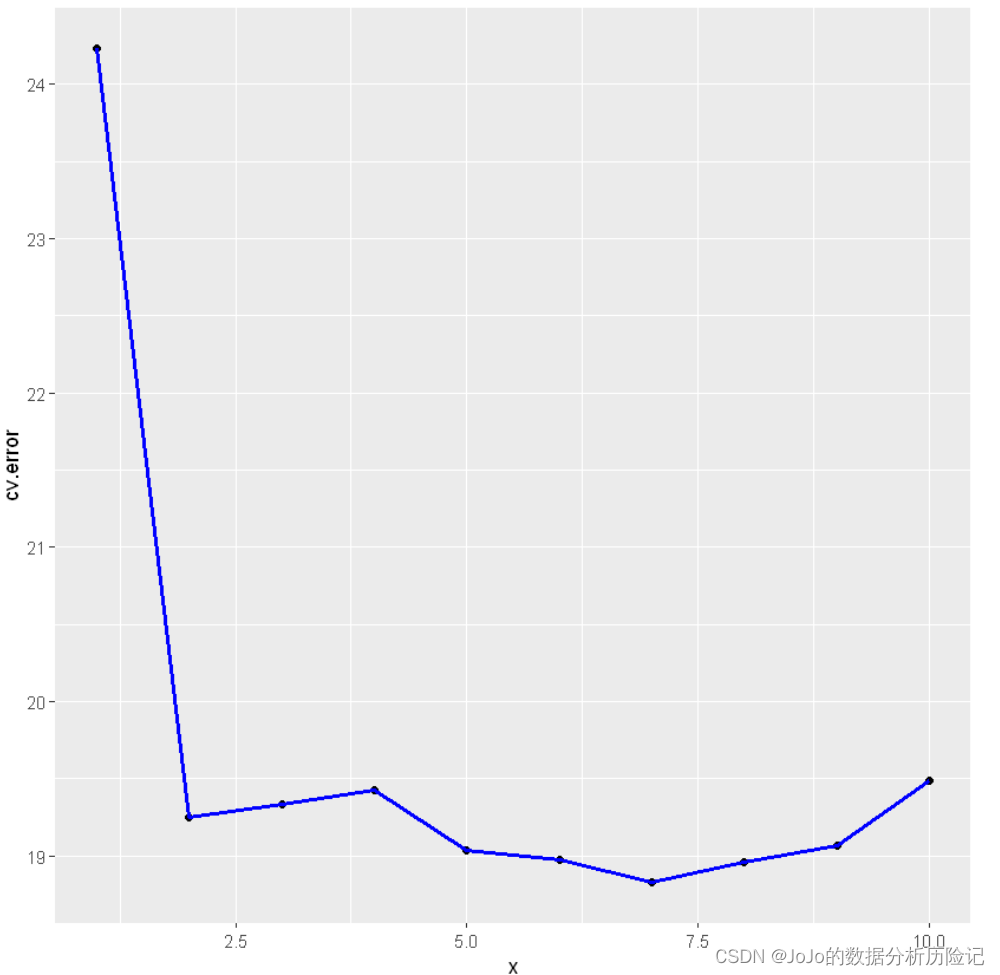
The results show that the error rate decreases greatly when fitting twice , This and K Fold cross validation is consistent
Now let's visualize the results
loocv <- data.frame(x,cv=cv.error)
library(ggplot2)
ggplot(loocv, aes(x, cv.error)) +geom_point() + geom_line(lwd=1,col='blue')
5. summary
We said K Folding cross validation is better in operation than leaving one method cross validation . But excluding the amount of computation , Another important advantage is that usually k The estimation of test error by fold cross validation is more accurate than that by leave one method .
We talked about that before , Leaving one method for cross validation is almost unbiased , Because he used n-1 Data training . alike k Fold cross validation whether k=5 and k=10 Will lead to a certain deviation . If only from the perspective of deviation , Leaving one method seems to perform better . But we also have to consider the problem of variance . about LOOCV, We are actually averaging the output of the fitting model , Each model is trained on almost the same observation set ; therefore , These outputs are highly relative to each other ( just ) relevant . by comparison , When we're in k<n In case of execution K fold CV when , We have little correlation with each other k The outputs of the two fitting models are averaged . Because the training set coincidence degree of each model is small . therefore LOOCV There will be a large variance . One way to improve the estimated variance is to get more samples . So , We no longer need to divide the training set into non overlapping sets . contrary , We will choose random K Sets of the same size .
in general ,K Fold cross validation takes k=5 or k=10 It's a good level , The variance and deviation are small .
This is the introduction of this chapter , If it helps you , Please do more thumb up 、 Collection 、 Comment on 、 Focus on supporting !!
边栏推荐
- Node の MongoDB安装
- 华昊中天冲刺科创板:年亏2.8亿拟募资15亿 贝达药业是股东
- Getting started with the go language is simple: go implements the Caesar password
- 源码编译安装MySQL
- 安装Mysql
- 【R语言数据科学】:交叉验证再回首
- remount of the / superblock failed: Permission denied
- ViewBinding和DataBinding的理解和区别
- Doctoral application | West Lake University Learning and reasoning system laboratory recruits postdoctoral / doctoral / research internship, etc
- 吃透Chisel语言.05.Chisel基础(二)——组合电路与运算符
猜你喜欢

Interviewer: what is the internal implementation of hash data type in redis?
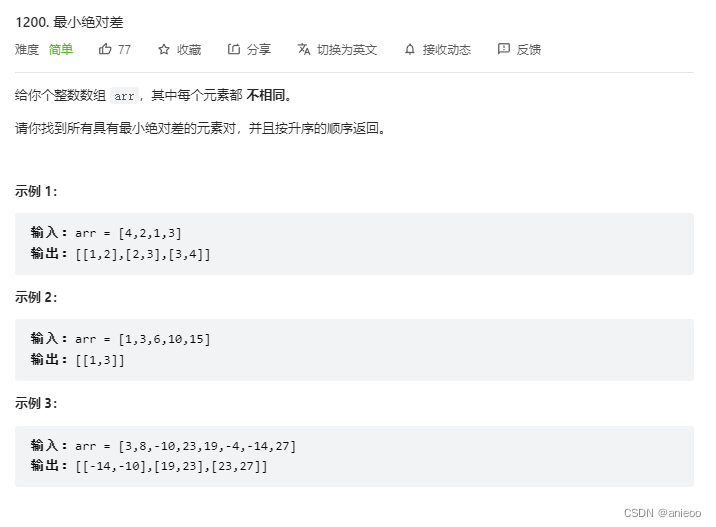
1200. 最小绝对差
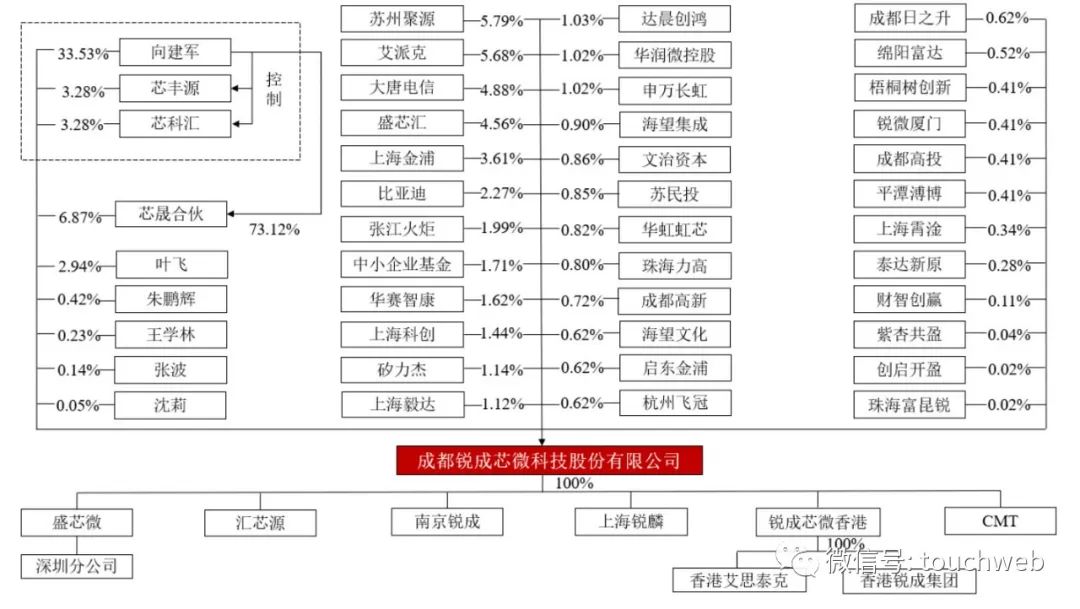
Ruichengxin micro sprint technology innovation board: annual revenue of 367million, proposed to raise 1.3 billion, Datang Telecom is a shareholder
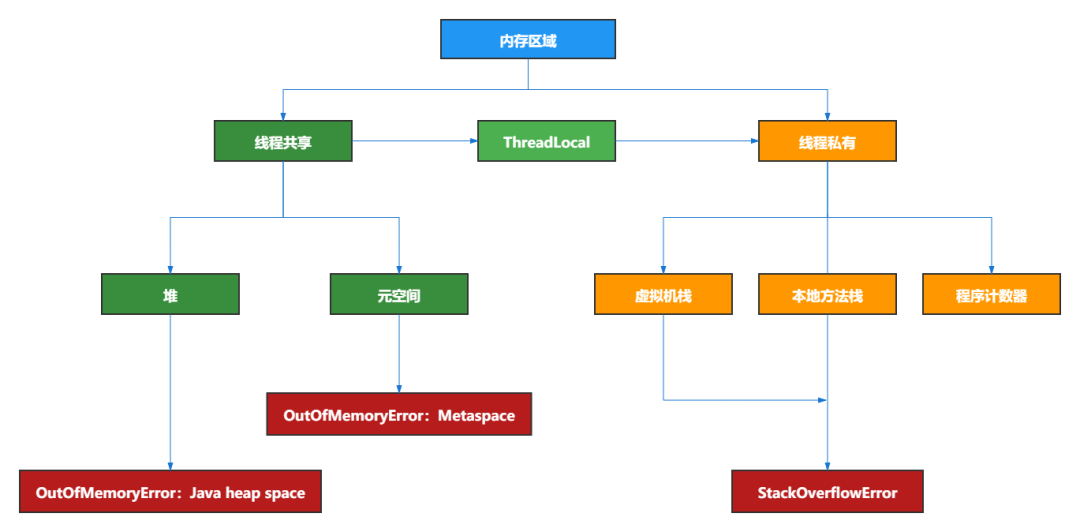
JVM 内存布局详解,图文并茂,写得太好了!

markdown 语法之字体标红
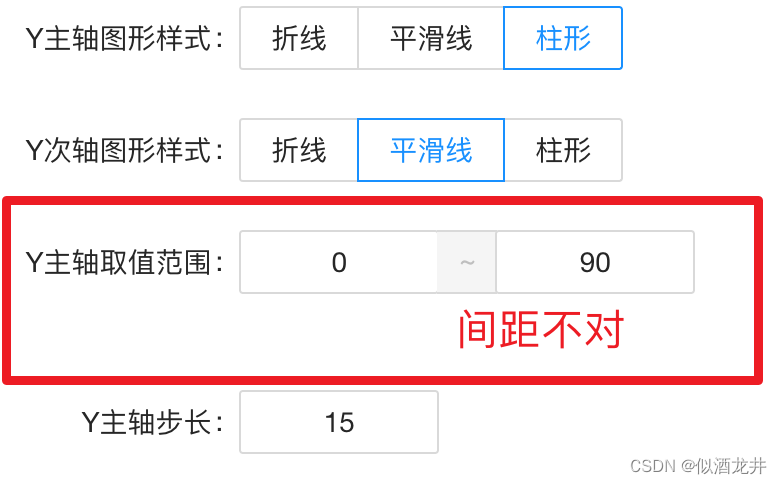
【Antd踩坑】Antd Form 配合Input.Group时出现Form.Item所占据的高度不对

Flet tutorial 03 basic introduction to filledbutton (tutorial includes source code) (tutorial includes source code)
. Net delay queue
吃透Chisel语言.11.Chisel项目构建、运行和测试(三)——Chisel测试之ScalaTest
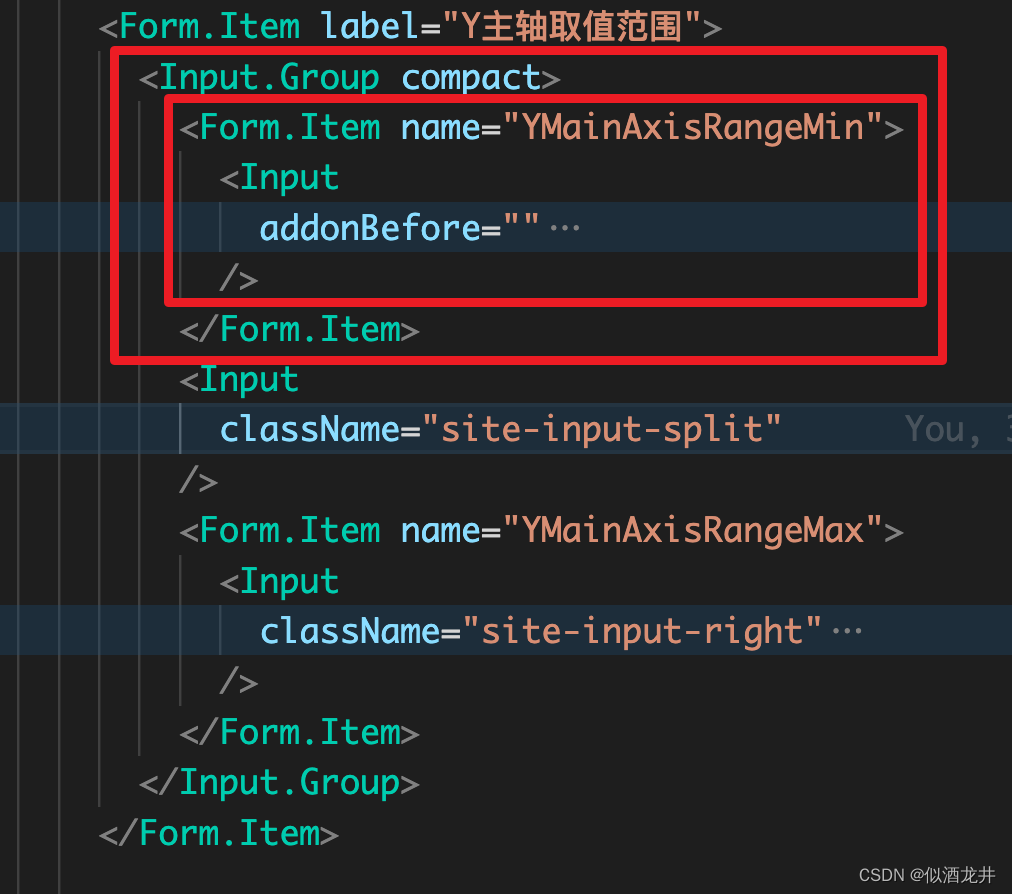
【Antd】Antd 如何在 Form.Item 中有 Input.Gourp 时获取 Input.Gourp 的每一个 Input 的value
随机推荐
C语言图书租赁管理系统
吃透Chisel语言.05.Chisel基础(二)——组合电路与运算符
Unittest框架中引入TestFixture
Fs4056 800mA charging IC domestic fast charging power IC
#yyds干货盘点# 解决名企真题:连续最大和
动画与过渡效果
Programmer anxiety
.Net之延迟队列
golang fmt.printf()(转)
Doctoral application | West Lake University Learning and reasoning system laboratory recruits postdoctoral / doctoral / research internship, etc
Fisher信息量检测对抗样本代码详解
美国土安全部部长警告移民“不要踏上危险的旅程”
安装Mysql
How to choose a technology stack for web applications in 2022
2022g3 boiler water treatment examination question simulation examination question bank and simulation examination
吃透Chisel语言.08.Chisel基础(五)——Wire、Reg和IO,以及如何理解Chisel生成硬件
Unittest框架之断言
OpenHarmony应用开发之如何创建DAYU200预览器
2022危险化学品经营单位主要负责人练习题及模拟考试
Haproxy high availability solution