当前位置:网站首页>Tree binary search tree
Tree binary search tree
2022-07-02 15:47:00 【-Xiaoxiaobai-】
- What is a tree
Tree is a very important data structure in computer , It is from n(n>=1) A hierarchical set of finite nodes . Only the trees linked by linked lists are discussed here .
Trees have the following characteristics
1. Each node has zero or more child nodes ;
2. A node without a parent node is the root node ;
3. Each non root node has only one parent node ;
4. Each node and its descendants can be regarded as a tree , A subtree called the parent of the current node ;
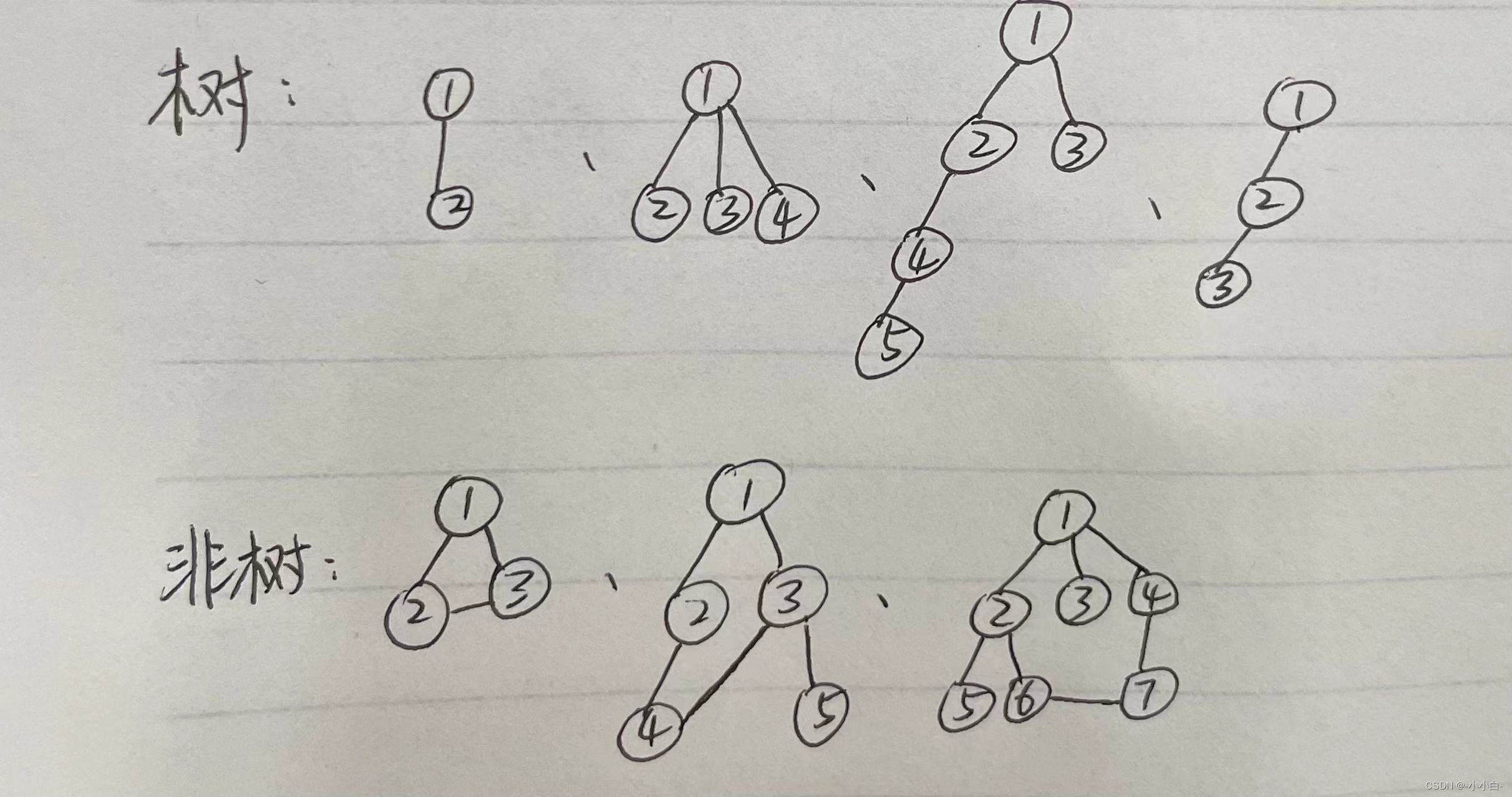
- Binary tree
If there are no more than two child nodes of each node of a tree , It can be said that this tree is a binary tree . The following figure is a standard binary tree .

Middle order traversal of binary trees
In the sequence traversal : Visit according to The left subtree —— The root node —— Right subtree The way to traverse the tree , And when you visit the left or right subtree , We traverse in the same way , Until you walk through the whole tree .

- For the tree in the above figure , The result of middle order traversal should be DBEAFCG-
Recursive implementation of middle order traversal ( Incoming root )
void inorder(TreeNode* T)
{
if(T == NULL){
return;
}
inorder(T->left);
printf("%d ", T->data);
inorder(T->right);
}Preorder traversal of two tree
The former sequence traversal : Visit according to The root node —— The left subtree —— Right subtree The way to traverse the tree , And when you visit the left or right subtree , We traverse in the same way , Until you walk through the whole tree .

- For the tree in the above figure , The result of preorder traversal should be ABDECFG-
Recursive implementation of middle order traversal ( Incoming root )
void inorder(TreeNode* T)
{
if(T == NULL){
return;
}
printf("%d ", T->data);
inorder(T->left);
inorder(T->right);
}Postorder traversal of binary trees
After the sequence traversal : Visit according to The left subtree —— Right subtree —— The root node The way to traverse the tree , And when you visit the left or right subtree , We traverse in the same way , Until you walk through the whole tree .

- For the tree in the above figure , The result of post order traversal should be DEBFGCA-
Recursive implementation of post order traversal ( Incoming root )
void inorder(TreeNode* T)
{
if(T == NULL){
return;
}
printf("%d ", T->data);
inorder(T->left);
inorder(T->right);
}Use the idea of preorder traversal to create a binary tree
void CreateTree(TreeNode** T)
{
int num;
scanf("%d", &num);
if(num == -1)
*T = NULL;
else
{
*T=(TreeNode*)malloc(sizeof(TreeNode));
(*T)->data = num;
CreateBiTree(&(*T)->left);
CreateBiTree(&(*T)->right);
}
}The incoming parameter is the address of the root node . Pay attention to the idea of traversing in the previous order when assigning values The root node —— The left subtree —— Right subtree To assign a value , Note that empty nodes cannot be skipped , Need to enter -1( Customize ) To represent the root node .

To create this binary tree , You need to enter... In turn A B D -1 -1 E -1 -1 C F -1 -1 G -1 -1.
Binary search ( lookup )( Sort ) Trees
The node placement rule of binary search tree is : The key value of any node must be greater than that of every node in its left subtree , And less than the key value of each node in its right subtree .
The existing sequence :A = {61, 87, 59, 47, 35, 73, 51, 98, 37, 93}. According to this sequence, the process of constructing binary search tree is as follows :
(1)i = 0,A[0] = 61, node 61 As root node ;
(2)i = 1,A[1] = 87,87 > 61, And nodes 61 The right child is empty , so 81 by 61 Node's right child ;
(3)i = 2,A[2] = 59,59 < 61, And nodes 61 The left child is empty , so 59 by 61 Node's left child ;
(4)i = 3,A[3] = 47,47 < 59, And nodes 59 The left child is empty , so 47 by 59 Node's left child ;
(5)i = 4,A[4] = 35,35 < 47, And nodes 47 The left child is empty , so 35 by 47 Node's left child ;
(6)i = 5,A[5] = 73,73 < 87, And nodes 87 The left child is empty , so 73 by 87 Node's left child ;
(7)i = 6,A[6] = 51,47 < 51, And nodes 47 The right child is empty , so 51 by 47 Node's right child ;
(8)i = 7,A[7] = 98,98 < 87, And nodes 87 The right child is empty , so 98 by 87 Node's right child ;
(9)i = 8,A[8] = 93,93 < 98, And nodes 98 The left child is empty , so 93 by 98 Node's left child ; After creation, it is shown in the figure 2.4 The binary search tree in :

The creation of binary search tree , Insert and delete
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
typedef struct BSTNode// Binary tree structure
{
int data;// Data fields
struct BSTNode *lchild,*rchild;// Left and right child pointer
}BSTNode,*BSTree;
void InitTree(BSTree &T)// Initialize binary sort tree
{
T = (BSTNode*)malloc(sizeof(BSTNode));// Create a header node
T->data = 0;
T->lchild = T->rchild = NULL;// Header pointer field NULL
}
void InsertTree(BSTree &T,int e)// Binary sort tree insertion
{
if(!T)// Find the insertion location , Recursion ends
{
BSTree S;
S = (BSTNode *)malloc(sizeof(BSTNode));// Create a node
S->data = e;// The data of the new node is set to e
S->lchild = S->rchild = NULL;// Set the new node as leaf node
T = S;// Put the new node S Connect to the found insertion position
}
else if(e<T->data)
InsertTree(T->lchild,e);// take S Insert the left subtree
else
InsertTree(T->rchild,e);// take S Insert right subtree
}
void CreateTree(BSTree &T)// Create a binary sort tree
{
int a;
printf(" Please enter :");
scanf("%d",&a);
T->data = a;// Fill the data into the root node of the binary sort tree
while(1)// Use a loop to insert
{
scanf("%d",&a);
InsertTree(T,a);// Import data into binary sort tree T in
if(getchar()=='\n')// Dead cycle end condition
break;
}
}
void InOrderTraverse(BSTree T)// Traversing the binary tree , In the sequence traversal
{
if(T)// The recursive termination condition is T by NULL
{
InOrderTraverse(T->lchild);// The middle order traverses the left subtree
printf("%d ",T->data);// Output print root node
InOrderTraverse(T->rchild);// The middle order traverses the right subtree
}
}
int SearchTree(BSTree T,int key)// Searching binary sorting tree , The search here can only know whether there is and in the binary tree key Equal value
{
if(T == NULL)// Find the end , And not with key Equal value
return 0;
else if(T->data==key)// Find the end , There are and in a binary tree key Equal value
return T->data;
else if(key<T->data)
return SearchTree(T->lchild,key);// Recursive left subtree
else
return SearchTree(T->rchild,key);// Recursive right subtree
}
void DeleteTree(BSTree &T,int key)// From the binary sort tree T Deleting keywords from is equal to key The node of , There are three situations for discussion
{
BSTree f,p;
p = T;
f = NULL;// initialization
while(p)// Use a loop to find keywords equal to key The node of
{
if(p->data == key)// Finding keywords equals key The node of , And out of the loop
break;
f = p;// node f Always a node p The parent node of
if(p->data>key)
p = p->lchild;// stay p Continue to search in the left subtree of
else
p = p->rchild;// stay p Continue to search in the right subtree of
}
if(p == NULL)// If the deleted node cannot be found, return
{
printf(" No value found to delete !\n");
return ;
}
/* Case one : Deleted node ( The node containing the deleted node is the root node ) There are both left and right subtrees of , Find the last node in the middle order on its left subtree to fill */
BSTree q,s;
if((p->lchild)&&(p->rchild))// Deleted node p Left and right subtrees are not empty
{
q = p;
s = p->rchild;
while(s->rchild)// At node p Continue to find its precursor node in the left subtree of , That is, the lowest right node
{
q = s;
s = s->rchild;// Right to the end
}
p->data = s->data;// node s The data in replaces the deleted node p Medium
if(q != p)// Reconnect nodes q The right subtree
q->rchild = s->lchild;
else// Reconnect nodes q The left subtree
q->lchild = s->lchild;
free(s);// Release s
return ;// End the function
}
/* The second case : Deleted node ( Contains the root node ) Lack of right subtree , And both left and right subtrees are missing ( That is, leaf node ); The missing right subtree is filled with the left child */
else if(p->rchild == NULL)// The deleted node lacks a right subtree
{
if(f)// Judge whether the deleted node is the root node , If so f==NULL
{
if(f->lchild == p)// Judge whether the left child of the parent node of the deleted node is p
{
f->lchild = p->lchild;
p->lchild = NULL;
}
else// The right child of the parent node of the deleted node is p
{
f->rchild = p->lchild;
p->lchild = NULL;
}
free(p);// Release nodes p
return ;// End the function
}
else// The deleted node is the root node
{
f = p;
p = p->lchild;
f->lchild = NULL;
free(f);// Release the root node
T = p;// Root node shift
return ;
}
}
/* The third case : Deleted node ( Contains the root node ) Missing left subtree , And both left and right subtrees are missing ( That is, leaf node ); Fill the left subtree with the right child */
else // else if(p->lchild == NULL)// The deleted node is missing the left subtree
{
if(f)// Judge whether the deleted node is the root node , If so f==NULL
{
if(f->lchild == p)// Judge whether the left child of the parent node of the deleted node is p
{
f->lchild = p->rchild;
p->rchild = NULL;
}
else// The right child of the parent node of the deleted node is p
{
f->rchild = p->rchild;
p->rchild = NULL;
}
free(p);// Release nodes p
return ;// End the function
}
else// The deleted node is the root node
{
f = p;
p = p->rchild;
f->lchild = NULL;
free(f);// Release the root node
T = p;// Root node shift
return ;// End the function
}
}
}
int main()
{
BSTree T;
InitTree(T);// Initialize binary sort tree
CreateTree(T);// Create a binary sort tree
InOrderTraverse(T);// Print
printf("\n");
if(SearchTree(T,16))// Determine whether there are keywords and... In the binary sort tree key Equal node , Among them 16 Is the test value , Commutative variables
printf(" There is :%d\n",SearchTree(T,16));
else
printf(" non-existent !\n");
DeleteTree(T,16);// Delete binary sorting tree , Delete and key Equal node , The value is the test value
printf(" After deleting :");
InOrderTraverse(T);// Print the results again , Verify that the deletion was successful
free(T);
return 0;
}
边栏推荐
- Analysis of the difference between array and linked list
- folium地图无法显示的问题,临时性解决方案如下
- 2278. Percentage of letters in string
- Solve the problem of base64encoder error
- 2279. Maximum number of backpacks filled with stones
- 【LeetCode】1254-统计封闭岛屿的数量
- 目标检测—利用labelimg制作自己的深度学习目标检测数据集
- [leetcode] 1905 statistics sub Island
- 高考录取分数线爬虫
- Folium, diagnosis and close contact trajectory above
猜你喜欢

【Salesforce】如何确认你的Salesforce版本?

Loss function and positive and negative sample allocation: Yolo series
《大学“电路分析基础”课程实验合集.实验四》丨线性电路特性的研究

Review materials for the special topic of analog electronics with all essence: basic amplification circuit knowledge points

Deux séquences ergodiques connues pour construire des arbres binaires
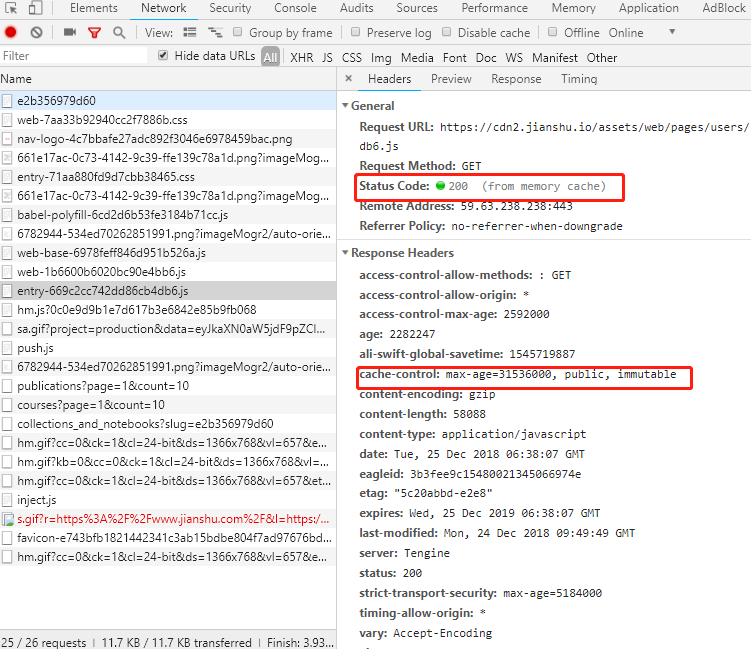
彻底弄懂浏览器强缓存和协商缓存

2022 年辽宁省大学生数学建模A、B、C题(相关论文及模型程序代码网盘下载)
Redux——详解

PHP static members

密码学基础知识
随机推荐
Pytoch saves tensor to Mat file
【LeetCode】1905-统计子岛屿
Pyinstaller打包exe附带图片的方法
2279. 装满石头的背包的最大数量
【LeetCode】1140-石子游戏II
folium,确诊和密接轨迹上图
【LeetCode】189-轮转数组
Astra: could not open "2bc5/ [email protected] /6“: Failed to set USB interface
folium地图无法显示的问题,临时性解决方案如下
[network security] network asset collection
【LeetCode】200-岛屿数量
/bin/ld: 找不到 -lxml2
fastjson List转JSONArray以及JSONArray转List「建议收藏」
(Video + graphic) machine learning introduction series - Chapter 5 machine learning practice
Analysis of the difference between array and linked list
Golang MD5 encryption and MD5 salt value encryption
全是精华的模电专题复习资料:基本放大电路知识点
2278. 字母在字符串中的百分比
PTA ladder game exercise set l2-001 inter city emergency rescue
College entrance examination admission score line crawler