当前位置:网站首页>[code source] daily question tree
[code source] daily question tree
2022-07-25 09:37:00 【self_ disc】
2022.05.07
Topic link : Trees - subject - Daimayuan Online Judge
Title Description :
There is a tree n The number of nodes is in 11 For rooted trees . You can now operate on this tree several times , Each operation can select a point in the tree and delete all edges between the point and its son .
Now I want to know for every k∈[1,n], At least how many operations are needed to make the graph happen to exist k A link block .
Input format
Enter a positive integer in the first line n.
Second line input n−1 It's an integer fi Express i+1 Father of point , Guarantee 1≤fi≤i.
Output format
Output n It's an integer , The first i The number means k=i The answer is , If you can't make the graph just exist k A link block , The output -1.
The sample input
6
1 2 1 1 2Sample output
0 -1 1 1 -1 2Data scale
common 10 A test point .
Test point 1,2,31,2,3 Satisfy n≤20.
Test point 4,5,64,5,6 Satisfy n≤100.
For all the data , Satisfy 1≤n≤3000.
analysis :
Delete a node , The number of connected blocks increases the number of child nodes of the node . that , We regard each node as an object , The value of an item is the number of child nodes . The knapsack capacity is the number of connected blocks .
f[i] Express i The minimum number of operations required for connected blocks .
Transfer equation :f[i]=min(f[i],f[i-a[i]]+1).
See the code for details. :
#include <bits/stdc++.h>
using namespace std;
const int mod = 1e9 + 7;
#define ll long long
int n, a[3009], f[3009];
void solve()
{
cin >> n;
for (int i = 2; i <= n; i++)
{
int x;
cin >> x;
a[x]++; // Count the number of child nodes
}
memset(f, 127, sizeof(f)); // The initial setting is infinite
f[1] = 0; // Initial is 1 A connecting block , Without the operating
for (int i = 1; i <= n; i++)
{
if (a[i]) // Has child nodes
{
for (int j = n; j >= a[i]; j--)
{
f[j] = min(f[j], f[j - a[i]] + 1); // 01 knapsack
}
}
}
for (int i = 1; i <= n; i++) // Output
if (f[i] < 9999999)
cout << f[i] << " \n"[i == n];
else
cout << -1 << " \n"[i == n];
}
int main()
{
ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
solve();
}边栏推荐
猜你喜欢

*6-3 节约小能手
![[De1CTF 2019]SSRF Me](/img/12/44c37cc713b49172a10579c9628c94.png)
[De1CTF 2019]SSRF Me

Thick willow dustpan, thin willow bucket, who hates reptile man? Asynchronous synergism, half a second to strip away a novel

作业7.15 shell脚本
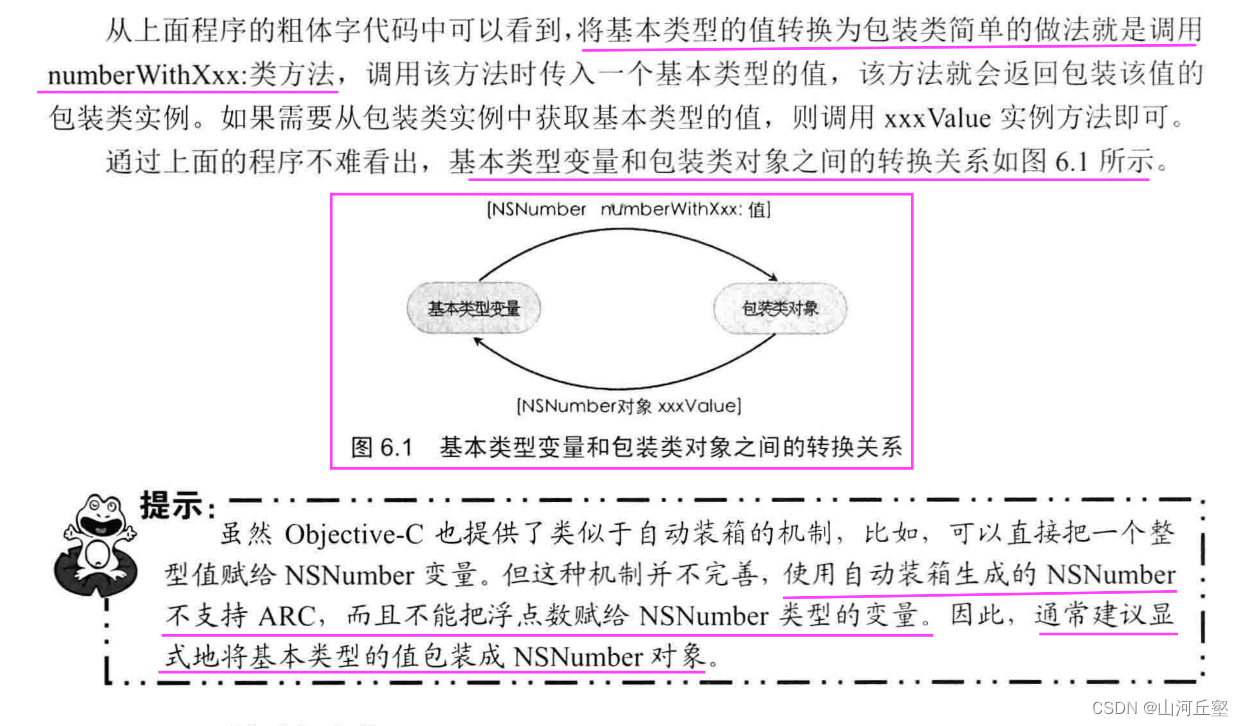
OC--包装类和处理对象
学习 Redis linux 安装Redis

uni-app如何获取位置信息(经纬度)

Object initialization
自定义Dialog 实现 仿网易云音乐的隐私条款声明弹框

UI - infinite rotation chart and column controller
随机推荐
Indexes, views and transactions of MySQL
matplotlib数据可视化三分钟入门,半小时入魔?
Job 7.15 shell script
变量名可以用中文?直接把人干蒙了
自定义Dialog 实现 仿网易云音乐的隐私条款声明弹框
Class (2) and protocol
【代码源】每日一题 国家铁路
@3-2 CCF 2020-12-2 期末预测之最佳阈值
Flex layout syntax and use cases
链表--基本操作
@3-1 CCF 2020-09-1 称检测点查询
*7-1 CCF 2015-09-1 数列分段
Understand the execution process of try, catch and finally (including return) (the most detailed analysis of the whole network)
js中map()函数的使用
OC--Foundation--数组
SurfaceView 闪屏(黑一下问题)
OC -- category extension agreement and delegation
Definition of cell
OC--包装类和处理对象
[code source] daily question - queue