[1206. Design skip table]

source ： Power button （LeetCode）

describe ：

Do not use any library functions , To design a Jump watch .
The data structure of jump table is composed of William Pugh Invented , For a detailed introduction of the skip table, please refer to the paper : Skip Lists: A Probabilistic Alternative to Balanced Trees

Jump watch Is in O(log(n)) Add... In time 、 Delete 、 The data structure of the search operation . Compared with tree pile and red black tree , Its function and performance are equivalent , And the code length of the jump table is shorter , Its design idea is similar to the linked list .

for example , A jump table contains [30, 40, 50, 60, 70, 90] , Then increase 80、45 To jump table , Operate as shown in the following figure ：

There are many layers in the jump table , Each layer is a short linked list . Under the action of the first layer , increase 、 The time complexity of deletion and search operations does not exceed O(n). The average time complexity of each operation of the jump table is O(log(n)), The space complexity is O(n).

In the subject , Your design should include these functions ：

• bool search(int target) : return target Whether it exists in the jump table .
• void add(int num): Insert an element into the jump table .
• bool erase(int num): Delete a value in the jump table , If num non-existent , Go straight back to false. If there are multiple num , Any one of them can be deleted .

Be careful , There may be multiple identical values in the jump table , Your code needs to handle this situation .

Example 1:

 Input 
["Skiplist", "add", "add", "add", "search", "add", "search", "erase", "erase", "search"]
[[], [1], [2], [3], [0], [4], [1], [0], [1], [1]]
 Output 
[null, null, null, null, false, null, true, false, true, false]

 explain 
Skiplist skiplist = new Skiplist();
skiplist.add(1);
skiplist.add(2);
skiplist.add(3);
skiplist.search(0);   //  return  false
skiplist.add(4);
skiplist.search(1);   //  return  true
skiplist.erase(0);    //  return  false,0  Not in the jump table 
skiplist.erase(1);    //  return  true
skiplist.search(1);   //  return  false,1  Has been erased 

Tips :

• 0 <= num, target <= 2 * 10⁴

• call search, add, erase The number of operations shall not be greater than 5 * 10⁴

Method ： Direct structure

Jump table is a kind of randomized data structure , It can be regarded as a variety of binary tree , It's in performance with the red black tree 、 AVL A tree is equal to a tree , But the principle of meter jumping is very simple , Currently in Redis and LevelDB All of them are useful for . The expected space complexity of the jump table is O(n), Jump table query , The expected time complexity of the insert and delete operations is O(logn). The jump table is actually a multi-layer ordered linked list , Each layer of the jump list is an ordered linked list , And satisfy that each is located in i The nodes of the layer are pp The probability of appearing in the second i + 1 layer , among p Constant .

Its structure is similar to that shown in the figure below :

Jump table when searching , First, from the current top L(n) Layer starts to look up , Compare one by one at the current level until the next node of the current node is greater than or equal to the target node , Then move to the next level to find , Repeat this process until you reach the first floor . here , If the next node is the target node , Then the search is successful ; conversely , Then the element does not exist . Since you start searching from the top to the bottom , Because the elements appearing at the lower level may not appear at the higher level , Therefore, the skip table will skip some elements in the process of searching , Compared with the query of ordered linked list , The query speed of jump table will be faster .
Jump table initialization 、 lookup 、 add to 、 The deletion operation is described in detail as follows ：

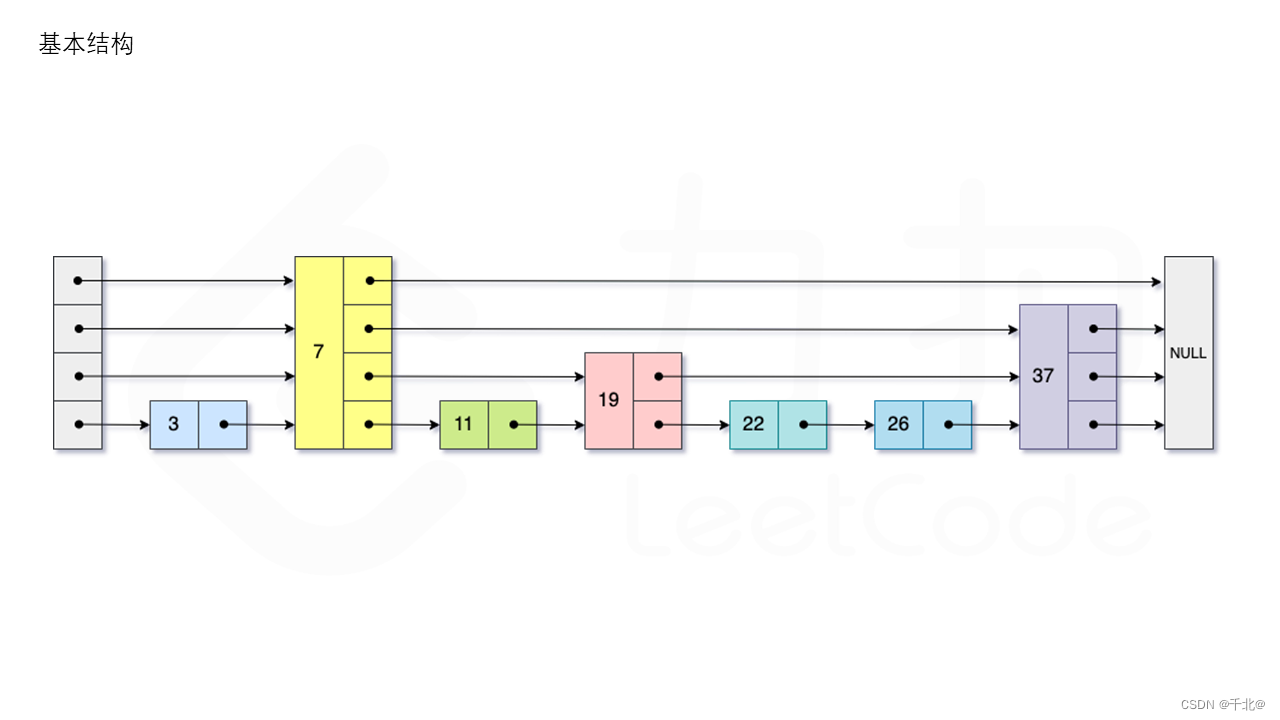
• search： The current maximum number of layers from the jump table level Layer starts to look up , Compare one by one at the current level until the next node of the current node is greater than or equal to the target node , Then move to the next level to find , Repeat this process until you reach the 1 layer . here , Ruodi 1 The value of the next node of the layer is equal to target, Then return to true; conversely , Then return to false. As shown in the figure ：
  
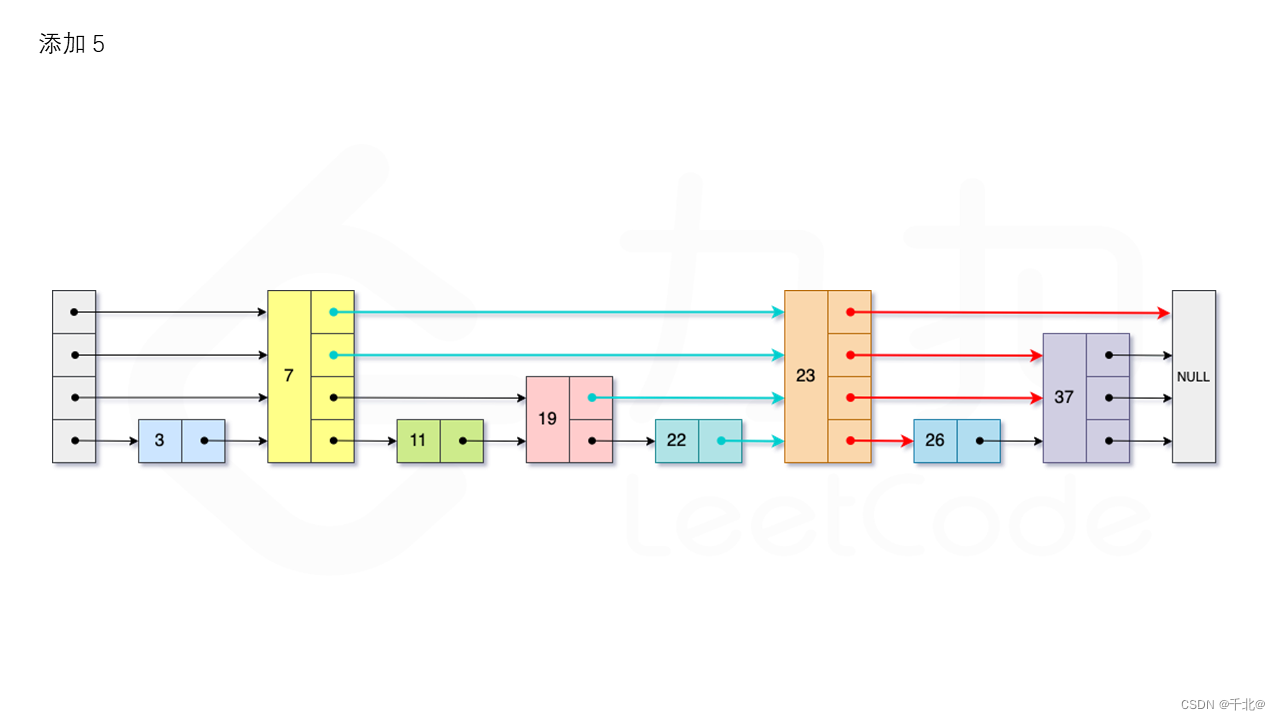
• add： The current maximum number of layers from the jump table level Layer starts to look up , Compare one by one at the current level until the next node of the current node is greater than or equal to the target node , Then move to the next level to find , Repeat this process until you reach the 1 layer . Set the newly added node as newNode, We need to calculate the number of layers of nodes inserted this time lv, If level Less than lv, It also needs to be updated level. We use arrays update Save the last node found in each layer , The first i The last node of the layer is update[i]. We will newNode The subsequent nodes of point to update[i] The next node of , Simultaneous updating update[i] The subsequent nodes are newNode. As shown in the figure ：
  

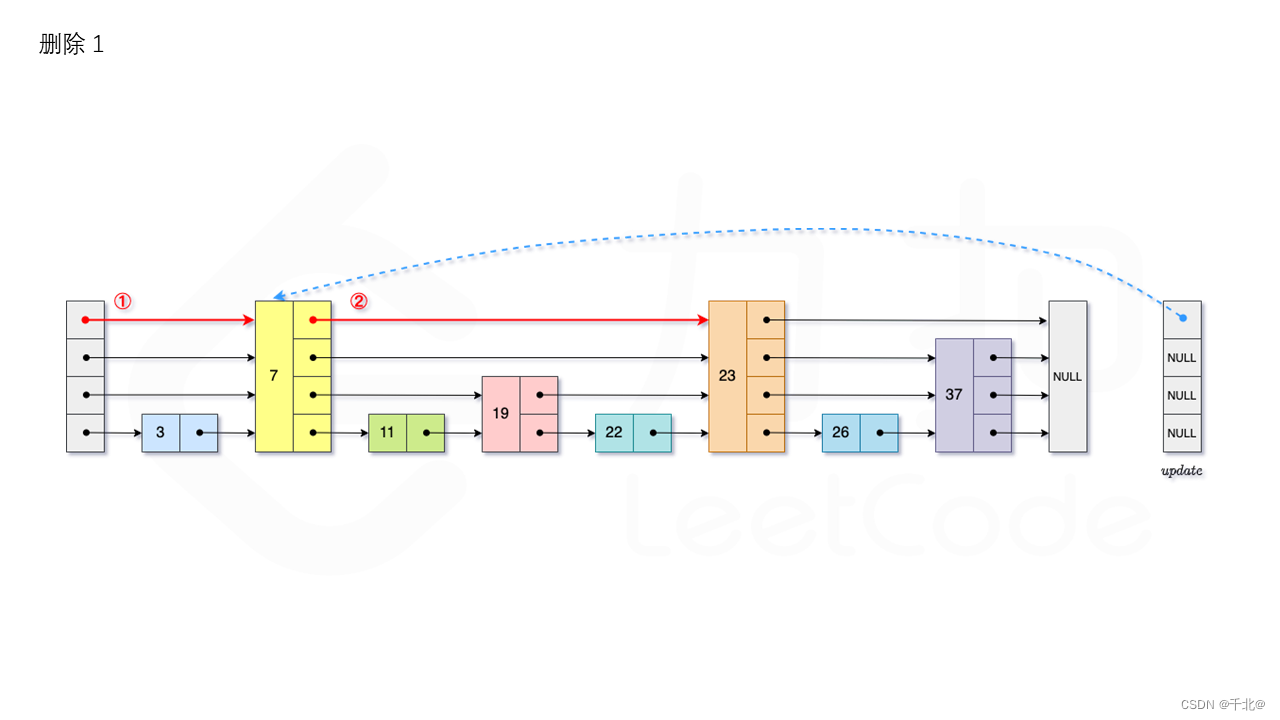
• erase： First, we need to find out whether the current element exists in the jump table . The current maximum number of layers from the jump table level Layer starts to look up , Compare one by one at the current level until the next node of the current node is greater than or equal to the target node , Then move to the next level to find , Repeat this process until you reach the 1 layer . If the first 1 The next node of the layer is not equal to num when , It means that the current element does not exist and returns directly . We use arrays update Save the last node found in each layer , The first i The last node of the layer is update[i]. At this time i The value of the next node of the layer is num, Then we need to delete it from the jump table . Due to the first i Layer with p The probability of appearing in the second i + 1 layer , Therefore, we should start from 1 The layer starts to update up , take num from update[i] Delete in the next jump of , Simultaneous updating update[i] Subsequent node , Until the linked list of the current layer does not appear num The node of . Finally, we need to update the current maximum number of layers in the jump table level. As shown in the figure ：

Code ：

constexpr int MAX_LEVEL = 32;
constexpr double P_FACTOR = 0.25;

struct SkiplistNode {
    
    int val;
    vector<SkiplistNode *> forward;
    SkiplistNode(int _val, int _maxLevel = MAX_LEVEL) : val(_val), forward(_maxLevel, nullptr) {
    
        
    }
};

class Skiplist {
    
private:
    SkiplistNode * head;
    int level;
    mt19937 gen{
    random_device{
    }()};
    uniform_real_distribution<double> dis;

public:
    Skiplist(): head(new SkiplistNode(-1)), level(0), dis(0, 1) {
    

    }

    bool search(int target) {
    
        SkiplistNode *curr = this->head;
        for (int i = level - 1; i >= 0; i--) {
    
            /*  Find No  i  The layer is smaller than and closest to  target  The elements of */
            while (curr->forward[i] && curr->forward[i]->val < target) {
    
                curr = curr->forward[i];
            }
        }
        curr = curr->forward[0];
        /*  Detect whether the value of the current element is equal to  target */
        if (curr && curr->val == target) {
    
            return true;
        } 
        return false;
    }

    void add(int num) {
    
        vector<SkiplistNode *> update(MAX_LEVEL, head);
        SkiplistNode *curr = this->head;
        for (int i = level - 1; i >= 0; i--) {
    
            /*  Find No  i  The layer is smaller than and closest to  num  The elements of */
            while (curr->forward[i] && curr->forward[i]->val < num) {
    
                curr = curr->forward[i];
            }
            update[i] = curr;
        }
        int lv = randomLevel();
        level = max(level, lv);
        SkiplistNode *newNode = new SkiplistNode(num, lv);
        for (int i = 0; i < lv; i++) {
    
            /*  Right.  i  Update the status of the layer , Change the current element's  forward  Point to new node  */
            newNode->forward[i] = update[i]->forward[i];
            update[i]->forward[i] = newNode;
        }
    }

    bool erase(int num) {
    
        vector<SkiplistNode *> update(MAX_LEVEL, nullptr);
        SkiplistNode *curr = this->head;
        for (int i = level - 1; i >= 0; i--) {
    
            /*  Find No  i  The layer is smaller than and closest to  num  The elements of */
            while (curr->forward[i] && curr->forward[i]->val < num) {
    
                curr = curr->forward[i];
            }
            update[i] = curr;
        }
        curr = curr->forward[0];
        /*  If the value does not exist, it returns  false */
        if (!curr || curr->val != num) {
    
            return false;
        }
        for (int i = 0; i < level; i++) {
    
            if (update[i]->forward[i] != curr) {
    
                break;
            }
            /*  Right.  i  Update the status of the layer , take  forward  Point to the next hop of the deleted node  */
            update[i]->forward[i] = curr->forward[i];
        }
        delete curr;
        /*  Update the current  level */
        while (level > 1 && head->forward[level - 1] == nullptr) {
    
            level--;
        }
        return true;
    }

    int randomLevel() {
    
        int lv = 1;
        /*  Random generation  lv */
        while (dis(gen) < P_FACTOR && lv < MAX_LEVEL) {
    
            lv++;
        }
        return lv;
    }
};

Execution time ：68 ms, In all C++ Defeated in submission 66.62% Users of
Memory consumption ：37.4 MB, In all C++ Defeated in submission 26.23% Users of
Complexity analysis
Time complexity ： O(logn), among n by add Number of calls . Detailed analysis of reference problem solution description .
Spatial complexity ： O(n), among n by add Number of calls . Detailed analysis of reference problem solution description .