当前位置:网站首页>编码与进制
编码与进制
2022-07-30 22:16:00 【张子虚】
编码浅谈
引
有这样一句俗语: ”没有前面那个1,后面多少个0都无意义“
正
多项式
先从多项式讲起,一个数值可以表现出多项式的形式,如例1:
27017 = 2 × 1 0 4 + 7 × 1 0 3 + 0 × 1 0 2 + 1 × 1 0 1 + 7 × 1 0 0 27017 = 2 \times 10^4 + 7 \times 10^3 + 0 \times 10^2 + 1 \times 10 ^1 + 7 \times 10^0 27017=2×104+7×103+0×102+1×101+7×100
多项式的数学定义:
a 1 x n − 1 + a 2 x n − 2 + a 3 x n − 3 + … + a n x 0 a_1\large x^{n-1} + a_2\large x^{n-2} + a_3\large x^{n-3} + \ldots + a_n\large x^{0} a1xn−1+a2xn−2+a3xn−3+…+anx0
多项式在计算机程序中的表示:用一个变量表示多项式的基 var base = x \large _{}x x,用一个数组表示系数 var arr = [a1, a2, a3, … , an],数组的长度就是项数 n
任何一个数字都可以用不同 base 的多项式表示,所以一个多项式也可以转换为另一个不同 base 的多项式
对于例1,base = 10 则表现为[2, 7, 0, 1, 7]
Tips: 对于base = 10, arr = [0, 0, 3, 2, 5], 我们可以知道其值为325, 但如果是325, 是无法表现出[0, 0, 3, 2, 5], 也就是说,某些情况下,该运算不具有计算机程序中的可逆性
问题1:给定一个多项式,base已知,系数数组已知,如果要把它转换为另一个base2的多项式,base2 < base,那么base2需要一个多大的数组表示?
高base转低base,项数肯定会增多。首先,假设第一个多项式 base = b1 共 n 项,转换为第二个多项式 base = b2 共 m 项,现在就是要计算 m 的值。
一个多项式 X X X,base = b 1 b_1 b1 有 n n n项,则它的值保持在: b 1 n − 1 < = X < = b 1 n − 1 b_1^{n-1}<=X<=b_1^{n}-1 b1n−1<=X<=b1n−1
想要转化为 base = b 2 b_2 b2,假设有 m m m项,则它的值保持在: b 2 m − 1 < = X ′ < = b 2 m − 1 b_2^{m-1}<=X'<=b_2^{m}-1 b2m−1<=X′<=b2m−1,则可得出如下判断:
{ b 2 m − 1 < = b 1 n − 1 b 2 m > = b 1 n \begin{cases} b_2^{m-1}<=b_1^{n-1}\\ b_2^{m}>=b_1^{n}\\ \end{cases} { b2m−1<=b1n−1b2m>=b1n
化简得到:
{ m < = n l n b 1 l n b 2 ( m 向上取整 ) m > = ( n − 1 ) l n b 1 l n b 2 + 1 ( m 向下取整 ) \begin{cases} m<=n\frac{lnb_1}{lnb_2}(m向上取整)\\ m>=(n-1)\frac{lnb_1}{lnb_2}+1(m向下取整)\\ \end{cases} { m<=nlnb2lnb1(m向上取整)m>=(n−1)lnb2lnb1+1(m向下取整)
这里,我们需要考虑的是 m m m向上取整这个条件。因此,对于给定的多项式(base和n都已知),我们如果要得到base= b 2 b_2 b2对应的多项式表示,则 m m m的值为:
function m(b1, b2, n) {
return Math.ceil(n * Math.log(b1) / Math.log(b2))
}
问题2:给定一个多项式,base已知,系数数组已知,如何用程序转换为另一个已知base2(base2 < base)的多项式?
首先,假设第一个多项式 base = b1 共 n 项,转换为第二个多项式 base = b2 共 m 项,m已经在上一步计算出来了。
第一个多项式可以表示为
( ( ( ( a 1 b 1 + a 2 ) b 1 + a 3 ) b 1 + a 4 ) b 1 + … a n − 1 ) b 1 + a n ((((a_1b_1+a_2)b_1+a_3)b_1+a_4)b1+\ldots a_{n-1})b_1+a_n ((((a1b1+a2)b1+a3)b1+a4)b1+…an−1)b1+an
然后,将 a 1 a_1 a1转化为 b 2 b_2 b2多项式,类似与 a 1 = c 1 × b 2 t − 1 + c 2 × b 2 t − 2 + … + c n × b 2 0 a_1 = c_1 \times b_2^{t-1} + c_2 \times b_2^{t-2} + \ldots + c_n \times b_2^{0} a1=c1×b2t−1+c2×b2t−2+…+cn×b20 得到数组arr,每一项都小于 b 2 b_2 b2,该多项式的和为 a 1 a_1 a1
操作数组末位 c n c_n cn ( c n × b 1 + a 2 ) ÷ b 2 (c_n \times b_1 + a_2) \div b_2 (cn×b1+a2)÷b2,结果作为新的 a 2 a_2 a2, 余数保留(unshift)到新数组arr2中,重复该行为,直到arr的首位被处理,将余数和结果依次保留(unshift)到新数组arr2中。此时,得到了 a 1 b 1 + a 2 a_1b_1+a_2 a1b1+a2的多项式数组
然后如此重复,直到计算完 a n a_n an项
程序如下:
const PolynomialTransformation = (base1, arr1, base2) => {
//先排除开头的0
let start = 0;
for(let i = 0; i < arr1.length; i++){
if(arr1[i] !== 0){
break;
}
else{
start++;
}
}
//全0返回空数组
if(start === arr1.length){
return [];
}
let arr2Length = Math.ceil((arr1.length - start) * (Math.log(base1) / Math.log(base2)));
let arr2 = new Array(arr2Length).fill(0);
let stepLength = arr2.length - 1;
for (let i = 0; i < arr1.length; i++) {
let carry = arr1[i];
let place = arr2.length - 1;
while (true) {
carry += base1 * arr2[place];
// 计算a1的b2多项式
// 取余
arr2[place] = carry % base2;
// 获取进位数
carry = Math.floor(carry / base2);
if (carry === 0 && place <= stepLength){
stepLength = place;
break;
}
place--;
}
}
return arr2;
};
这个函数可以做到多项式在不同进制间的转化
对于一个确定的多项式:
base = 62, arr 为 `(16) [31, 27, 52, 6, 3, 21, 0, 9, 13, 27, 2, 46, 26, 57, 59, 22]
base = 256 arr为 `(12) [78, 34, 113, 96, 17, 249, 156, 67, 183, 15, 179, 84]`
按上述的内容,对于base = 62, arr 的字符串映射为 'vrQ63l09dr2KqVXm',欲要转化为256,在此时就已确定了其长度:
Math.ceil(16 * Math.log(62) / Math.log(256)) // 12
假设期望的是14个长度,则无法做到
可以看出,如果base = 62, 则这个函数的逻辑就是Base62编解码的实现细节
如果我们定义自己的map:
// default map
const map = '0123456789abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ'
就可以得到自定义的base62了。这个和base62.js中的逻辑类似,它也有自定义字符集的操作
It’s also possible to define a custom character set instead ——原文内容
用
Base62编解码一般用在哪些地方?
Base62编码是由10个数字、26个大写英文字母和26个小写英文字母组成,多用于安全领域和短URL生成。
短网址编码流程:
- 将长地址与一个整数(int64)建立映射(一对多)
- 对上一步的整数进行Base62编码(10进制转62进制)
- 拼接上域名
B站的av,bv码为Base58编码
Base64编码
Base64编码是用64(2的6次方)个ASCII字符来表示256(2的8次方)个ASCII字符,也就是三位二进制数组经过编码后变为四位的ASCII字符显示,长度比原来增加1/3。
Base64 编码是对二进制数据进行编码,表示成文本格式,且只包含 A-Z、a-z、0-9、+、/、=这些字符
原理:把 3 字节的二进制数据按 6bit 一组,用 4 个 int 整数表示,然后查表,把 int 整数用索引对应到字符,得到编码后的字符串。
区别
表格如下:
| 项 | base62 | base64 |
|---|---|---|
| 是否有进制转化 | 是 | 否 |
| 是否为流式处理 | 否 | 是 |
是否有header | 否 | 是 |
| 是否有事实标准 | 否 | 是 |
边栏推荐
- ML之shap:基于FIFA 2018 Statistics(2018年俄罗斯世界杯足球赛)球队比赛之星分类预测数据集利用RF随机森林+计算SHAP值单样本力图/依赖关系贡献图可视化实现可解释性之攻略
- MySQL 有这一篇就够(呕心狂敲37k字,只为博君一点赞!!!)
- StoneDB 为何敢称业界唯一开源的 MySQL 原生 HTAP 数据库?
- 史上超强最常用SQL语句大全
- cnpm installation steps
- 系统结构考点之并行计算霍纳法则
- 基于ABP实现DDD--实体创建和更新
- 【Network Security Column Directory】--Penguin Column Navigation
- mysql获取近7天,7周,7月,7年日期,根据当前时间获取近7天,7周,7月,7年日期
- 力扣题(3)—— 无重复字符的最长子串
猜你喜欢
【零代码工具】15 款企业级零代码开发平台推荐,总有一款是你心仪的

Uni-app 小程序 App 的广告变现之路:激励视频广告

【Untitled】

【导航规划】导航规划背景知识总结
It is enough for MySQL to have this article (disgusting typing 37k words, just for Bojun!!!)

A simple rich text editor
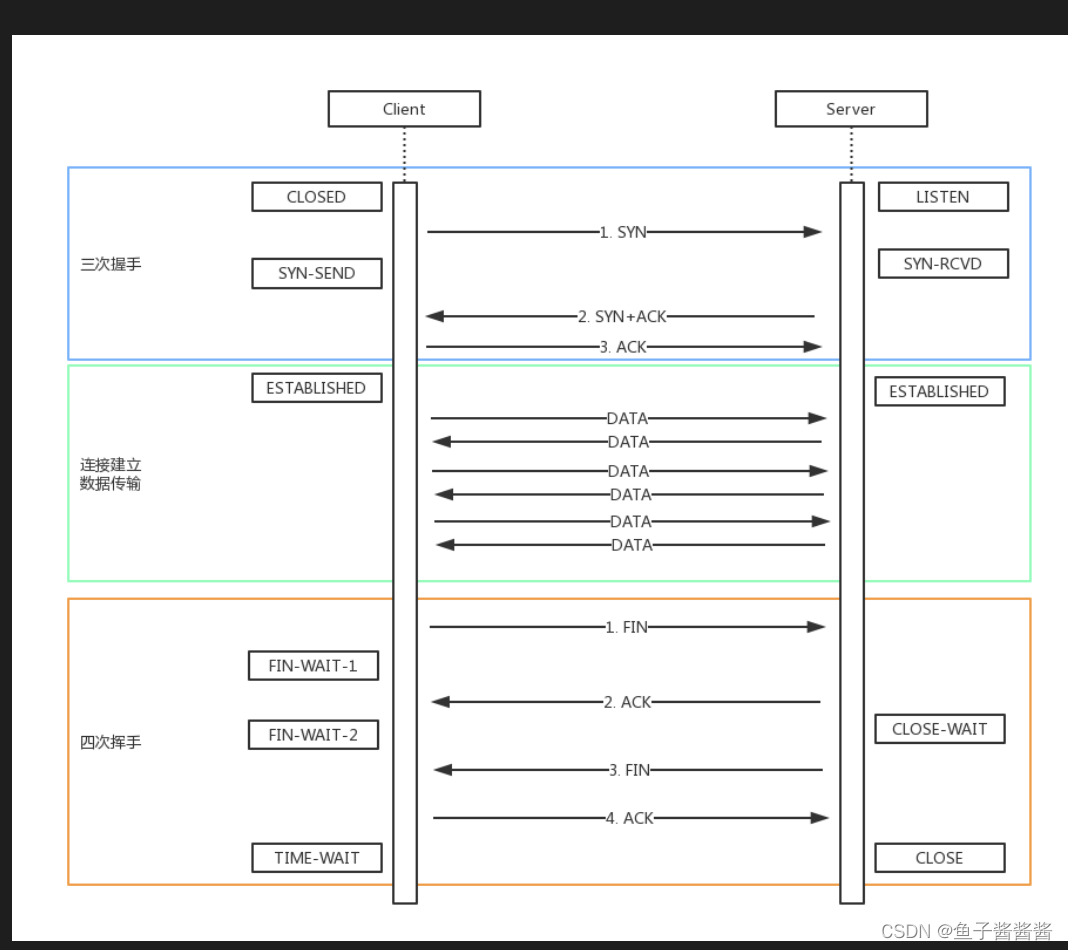
TCP 连接 三次握手 四次挥手

Ningbo Zhongning Pawn will transfer 29.5% of the equity for 2.8338 million yuan, and the owner's equity in 2021 will be 9.6875 million yuan

WSL2设置默认启动用户(debian)

NEOVIM下载安装与配置
随机推荐
language code table
成功解决ModuleNotFoundError: No module named ‘Image‘
The most complete Redis basic + advanced project combat summary notes in history
史上超强最常用SQL语句大全
解决npm warn config global `--global`, `--local` are deprecated. use `--location=global` instead
MySQL 8.0.29 set and modify the default password
2022.7.27
CISP-PTE Zhenti Demonstration
TransGAN代码复现—九天毕昇平台
MySQL 8.0.29 解压版安装教程(亲测有效)
mysql remove duplicate data
MySQL 用户授权
The Road to Ad Monetization for Uni-app Mini Program Apps: Rewarded Video Ads
The reason for not using bs4 is that the name is too long?Crawl lottery lottery information
About the data synchronization delay of MySQL master-slave replication
【Untitled】
MySQL联合查询(多表查询)
2022.7.30
QT开发简介、命名规范、signal&slot信号槽
PhpMetrics 使用