当前位置:网站首页>质数相关问题-小记
质数相关问题-小记
2022-08-02 14:10:00 【老顽固也可爱】
质数相关问题
质数又名素数,在ACM中经常出现相关问题,例如 P1029 NOIP2001 普及组 最大公约数和最小公倍数问题、P2043 质因子分解、P3383 【模板】线性筛素数 等等,今天就先来讲讲这几题目的共性。
奇技淫巧-欧几里得算法
欧几里得算法又称辗转相除法,是指用于计算两个非负整数a,b的最大公约数。应用领域有数学和计算机两个方面。计算公式 g c d ( a , b ) = g c d ( b , a m o d b ) gcd(a,b) = gcd(b,a mod b) gcd(a,b)=gcd(b,amodb) 。
inline int gcd(int x,int y)
{
if(y==0) return x;
return gcd(y,x%y);
}
例题如下:
[NOIP2001 普及组] 最大公约数和最小公倍数问题
题目描述
输入两个正整数 x 0 , y 0 x_0, y_0 x0,y0,求出满足下列条件的 P , Q P, Q P,Q 的个数:
P , Q P,Q P,Q 是正整数。
要求 P , Q P, Q P,Q 以 x 0 x_0 x0 为最大公约数,以 y 0 y_0 y0 为最小公倍数。
试求:满足条件的所有可能的 P , Q P, Q P,Q 的个数。
输入格式
一行两个正整数 x 0 , y 0 x_0, y_0 x0,y0。
输出格式
一行一个数,表示求出满足条件的 P , Q P, Q P,Q 的个数。
样例 #1
样例输入 #1
3 60
样例输出 #1
4
提示
P , Q P,Q P,Q 有 4 4 4 种:
- 3 , 60 3, 60 3,60。
- 15 , 12 15, 12 15,12。
- 12 , 15 12, 15 12,15。
- 60 , 3 60, 3 60,3。
对于 100 % 100\% 100% 的数据, 2 ≤ x 0 , y 0 ≤ 10 5 2 \le x_0, y_0 \le {10}^5 2≤x0,y0≤105。
【题目来源】
NOIP 2001 普及组第二题
题解
首先你需要先理解最大公约数和最小公倍数是怎么计算的。
要是 a a a 和 b b b 的 最大公约数为 m m m、最小公倍数为 n n n,则可以推断出 a ∗ b / m = n a*b/m=n a∗b/m=n ,而且 a / m a/m a/m 和 b / m b/m b/m 的 最大公约数是 1 1 1 。至于为什么?emmm,数学的直觉就是这样子的。
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
int sd(int a,int b)
{
if(a%b==0)
{
return b;
}
else
{
return sd(b,a%b);
}
}
int main()
{
int n,m;
while(~scanf("%d%d",&n,&m))
{
if(m%n!=0)
{
printf("0\n");
continue;
}
int k=m/n;
int sum=0;
for(int i=1;i<sqrt(k);i++)
{
if(k%i==0)
{
int q=k/i;
if(sd(q,i)==1)
{
sum++;
}
}
}
printf("%d\n",sum*2);
}
return 0;
}
质因子分解
题目描述
对N!进行质因子分解。
输入格式
输入数据仅有一行包含一个正整数N,N<=10000。
输出格式
输出数据包含若干行,每行两个正整数p,a,中间用一个空格隔开。表示N!包含a个质因子p,要求按p的值从小到大输出。
样例 #1
样例输入 #1
10
样例输出 #1
2 8
3 4
5 2
7 1
提示
10!=3628800=(28)*(34)*(5^2)*7
题解
这题就要用到质数的定义了,首先可以知道 一个数分解到最后一定是一堆质数的乘积。
那么假设这个数是 n n n ,就只要从 2 2 2 开始一直到 n n n 分解这个数,不用判断是不是质数,因为每个质因子我们都一直除,直到不能再除,以后也不会出现可以除的数是此数的倍数了,相当于已经筛掉了,所以最后一定会被分解成质数的乘积。
#include<iostream>
using namespace std;
int a[10001]={
0},n; //数组很大,记得开在外面哦
int main()
{
cin>>n;
for (int i=2;i<=n;i++) //1就不用了,从2到n一个一个来
{
int i2=i; //备份一下,不然等会被除掉了
for (int j=2;j<=i;j++) //从2开始判断是否可以整除
while (i2%j==0) {
a[j]++; i2/=j;}
//记得使用while,不是if,要一除到底
}
for (int i=1;i<=10000;i++) //输出
if (a[i]!=0)
cout<<i<<" "<<a[i]<<endl;
}
判断质数方法-总结
一个比较普通的判定方法
bool IsPrime()
{
for(int i=2;i<=sqrt(n);i++)
{
if(n%i==0) return false;
}
return true;
}
Eratosthenes筛选法(质数的倍数一定不是质数)
同时对于每个x,把大于等于x的平方的x的倍数标记为合数。
void isprime(int n)///筛选1-n的素数
{
memset(vis,0,sizeof(vis));
int m = sqrt(n + 0.5);
for(int i = 2; i <= m; i++)
{
if(!vis[i])
{
for(int j = i * i; j <= n; j += i)
vis[j] = 1;
}
}
}
线性筛法
每个合数只会被它的最小质因子筛一次,时间复杂度 O ( n ) O(n) O(n)
int v[maxn],prime[maxn];
void primes(int n)
{
memset(v,0,sizeof(v));///最小质因子
m=0;
for(i=2;i<=n;i++)
{
if(v[i]==0)///i为质数
{
v[i]=i;
prime[++m]=i;
}
///给当前的数i乘上一个质因子
for(j=1;j<=m;j++)
{
///i有比prime[i]更小的质因子,或者超出n的范围
if(prime[j]>v[i]||prime[j]>n/i) break;
v[i*prime[j]]=prime[j];
}
}
for(i=1;i<=m;i++)
cout<<prime[i]<<endl;
}
最快模板
还有一个在网上看到的一个判断素数的方法,这是当时ccpc的时候也用到过的一个模板。
bool isPrime( int num )
{
//两个较小数另外处理
if(num ==2|| num==3 )
return 1 ;
//不在6的倍数两侧的一定不是质数
if(num %6!= 1&&num %6!= 5)
return 0 ;
int tmp =sqrt( num);
//在6的倍数两侧的也可能不是质数
for(int i= 5;i <=tmp; i+=6 )
if(num %i== 0||num %(i+ 2)==0 )
return 0 ;
//排除所有,剩余的是质数
return 1 ;
}
这个算是我看到的判断素数最快的一种方法了
质数筛
对于一些求解第几个质数的问题,可以先打表,然后直接输出,这样会快一点。但是这种做法的时间一般大都都在之前的打表上,怎么减少打表的时间成了重中之重。下面这道题就是在解决这个问题。
【模板】线性筛素数
题目背景
本题已更新,从判断素数改为了查询第 k k k 小的素数
提示:如果你使用 cin 来读入,建议使用 std::ios::sync_with_stdio(0) 来加速。
题目描述
如题,给定一个范围 n n n,有 q q q 个询问,每次输出第 k k k 小的素数。
输入格式
第一行包含两个正整数 n , q n,q n,q,分别表示查询的范围和查询的个数。
接下来 q q q 行每行一个正整数 k k k,表示查询第 k k k 小的素数。
输出格式
输出 q q q 行,每行一个正整数表示答案。
样例 #1
样例输入 #1
100 5
1
2
3
4
5
样例输出 #1
2
3
5
7
11
提示
【数据范围】
对于 100 % 100\% 100% 的数据, n = 1 0 8 n = 10^8 n=108, 1 ≤ q ≤ 1 0 6 1 \le q \le 10^6 1≤q≤106,保证查询的素数不大于 n n n。
Data by NaCly_Fish.
#include <cstdio>
#include <cstring>
bool isPrime[100000010];
//isPrime[i] == 1表示:i是素数
int Prime[6000010], cnt = 0;
//Prime存质数
void GetPrime(int n)//筛到n
{
memset(isPrime, 1, sizeof(isPrime));
//以“每个数都是素数”为初始状态,逐个删去
isPrime[1] = 0;//1不是素数
for(int i = 2; i <= n; i++)
{
if(isPrime[i])//没筛掉
Prime[++cnt] = i; //i成为下一个素数
for(int j = 1; j <= cnt && i*Prime[j] <= n/*不超上限*/; j++)
{
//从Prime[1],即最小质数2开始,逐个枚举已知的质数,并期望Prime[j]是(i*Prime[j])的最小质因数
//当然,i肯定比Prime[j]大,因为Prime[j]是在i之前得出的
isPrime[i*Prime[j]] = 0;
if(i % Prime[j] == 0)//i中也含有Prime[j]这个因子
break; //重要步骤。见原理
}
}
}
int main()
{
int n, q;
scanf("%d %d", &n, &q);
GetPrime(n);
while (q--)
{
int k;
scanf("%d", &k);
printf("%d\n", Prime[k]);
}
return 0;
}
边栏推荐
- 刷卡芯片CI520可直接PIN对PIN替换CV520支持SPI通讯接口
- 2022TI杯D题混沌信号产生实验装置
- Golang 垃圾回收机制详解
- pytorch模型转libtorch和onnx格式的通用代码
- FP5139电池与适配器供电DC-DC隔离升降压电路反激电路电荷泵电路原理图
- 2020-02-06-快速搭建个人博客
- Please make sure you have the correct access rights and the repository exists. Problem solved
- Win10无法连接打印机怎么办?不能使用打印机的解决方法
- Letter combination of LeetCode2 phone number
- DP4056电源保护芯片锂电池pin对pinTP4056
猜你喜欢
随机推荐
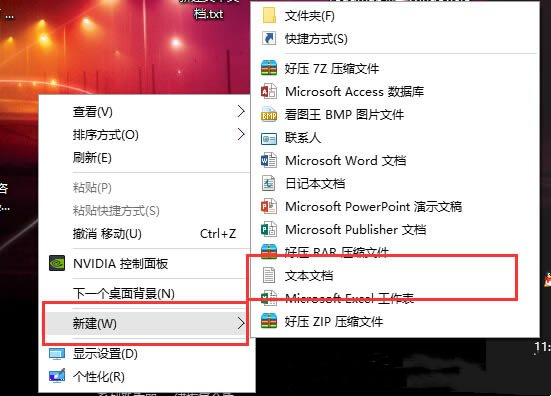
How to set the win10 taskbar does not merge icons
Actual combat Meituan Nuxt +Vue family bucket, server-side rendering, mailbox verification, passport authentication service, map API reference, mongodb, redis and other technical points
DP4056电源保护芯片锂电池pin对pinTP4056
vscode镜像
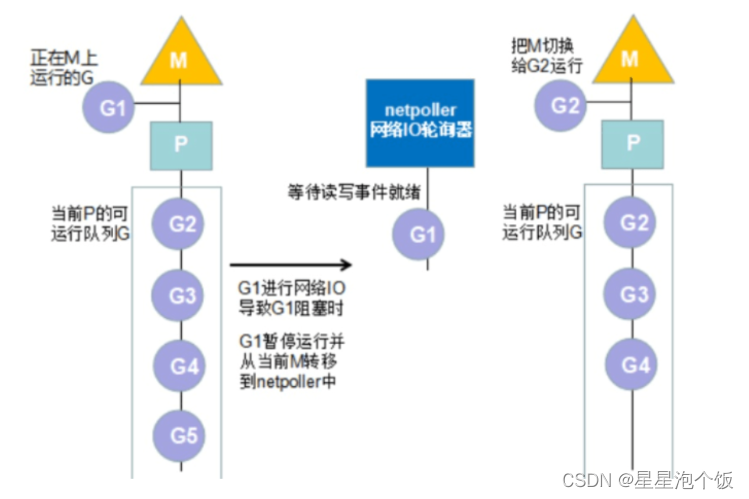
Golang 垃圾回收机制详解
如何用硬币模拟1/3的概率,以及任意概率?
General code for pytorch model to libtorch and onnx format
Spark及相关生态组件安装配置——快速回忆
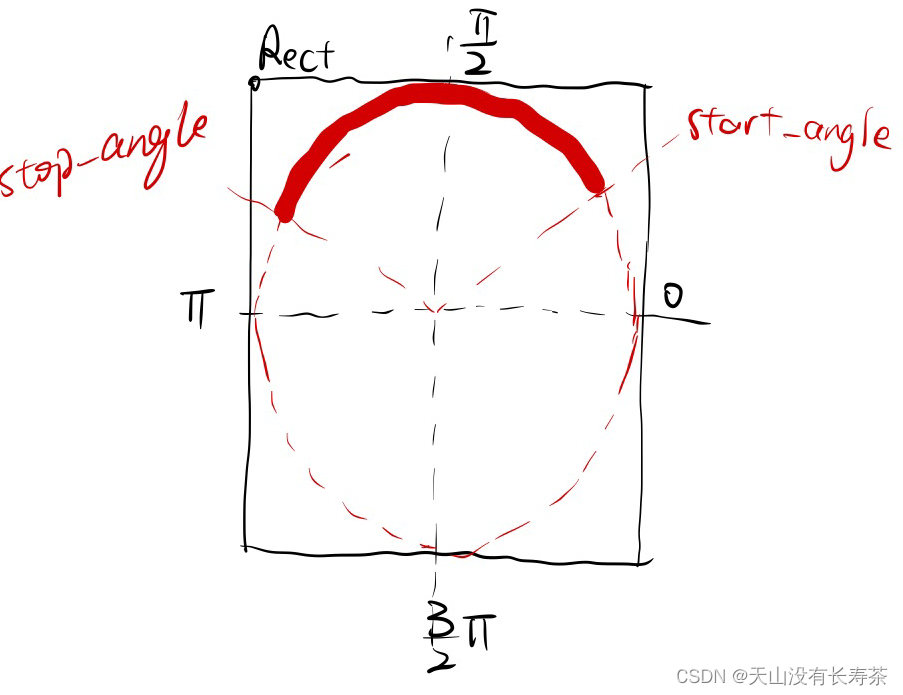
pygame draw arc
Bash shell位置参数
利用plot_surface命令绘制复杂曲面入门详解
ECP2459耐压60V降压BUCK电路用于WIFI模块供电方案原理图
倍增和稀疏表
Win7怎么干净启动?如何只加载基本服务启动Win7系统
What should I do if Windows 10 cannot connect to the printer?Solutions for not using the printer
Win11电脑一段时间不操作就断网怎么解决
Win10电脑需要安装杀毒软件吗?
Win11 keeps popping up User Account Control how to fix it
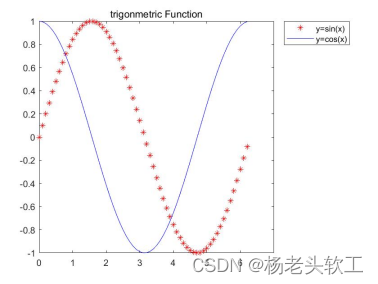
MATLAB绘图函数fplot详解
FP6293电池升压5V-12V大电流2APWM模式升压方案