当前位置:网站首页>模线性方程组(中国剩余定理+通用解法)
模线性方程组(中国剩余定理+通用解法)
2022-06-11 07:23:00 【CaptainHarryChen】
求解
中国剩余定理
若m1,m2,m3,...,mn m 1 , m 2 , m 3 , . . . , m n 两两互质,则可用中国剩余定理
设M=∏ni=1mi M = ∏ i = 1 n m i ,Mi=M/mi M i = M / m i ,ti t i 为Mi M i 在(mod mi) ( m o d m i ) 意义下的逆元,那么通解为
解释一下:
因为 tiMi≡1 (mod mi) t i M i ≡ 1 ( m o d m i ) ,而 Mj≡0 (mod mi) (j≠i) M j ≡ 0 ( m o d m i ) ( j ≠ i ) ,所以整个求和式子中,模 mi m i 有用的就只剩下 aitiMi≡ai (mod mi) a i t i M i ≡ a i ( m o d m i ) ,对每一个 mi m i 都如此,满足所有条件。
通用解法
不要求m1,m2,m3,...,mn m 1 , m 2 , m 3 , . . . , m n 两两互质的解法
首先考虑只有两个方程
则
用exgcd求不定方程,将 k1 k 1 , k2 k 2 解出,并带入原方程,得到一个特解 x x
可知这两个方程的通解 为
即
我们已经成功把两个方程合为一个,只需要继续把这个方程与方程组其他方程一一合并,就求出解了
模板题
HDU1573,求解的个数
#include<cstdio>
const int MAXM=13;
long long gcd(long long a,long long b,long long &x,long long &y)
{
if(b==0)
{
x=1;y=0;
return a;
}
long long xx,yy,d=gcd(b,a%b,xx,yy);
x=yy;
y=xx-a/b*yy;
return d;
}
long long a[MAXM],b[MAXM];
int main()
{
int T,M;
long long N,A,B,d,l,x,y,p,q,r;
scanf("%d",&T);
while(T--)
{
scanf("%I64d%d",&N,&M);
for(int i=1;i<=M;i++)
scanf("%I64d",a+i);
for(int i=1;i<=M;i++)
scanf("%I64d",b+i);
A=a[1];B=b[1];
bool flag=true;
for(int i=2;i<=M;i++)
{
p=A;q=a[i];r=b[i]-B;
d=gcd(p,q,x,y);
if(r%d)
{flag=false;break;}
p/=d;q/=d;r/=d;
x=x*r;
x=(x%q+q)%q;
l=A/d*a[i];
B=x*A+B;
B=(B%l+l)%l;
A=l;
if(B>N)break;
}
if(flag&&B<=N)
printf("%I64d\n",(N-B)/A+(B!=0));
else
puts("0");
}
return 0;
}边栏推荐
- Arduino_ Esp32 development record
- JVM learning record (VII) -- class loading process and parental delegation model
- gaussDB for redis和 redis的区别?
- MS office level II wrong question record [8]
- Post-processing of ffmpeg miscellaneous notes
- Biological sequence intelligent analysis platform blog (1)
- Leetcode-141. Linked List Cycle
- [STL source code analysis] summary notes (10): hashtable exploration
- Mistakes in Niuke JS exercise
- MySQL设置管理员密码无法生效的案例一则
猜你喜欢

Summary of classic interview questions

CMAP of Matplotlib
![[Oracle database] mammy tutorial day02 use of database management tool sqlplus](/img/f2/8f6f74a62427ebfb4c805c1e9b3352.png)
[Oracle database] mammy tutorial day02 use of database management tool sqlplus

No response from win10 explorer when dragging files
![20200727 T2 small w playing game [generating function (binomial inversion technique)]](/img/a5/ae2192f4f37232cdcb01e81ad0297c.jpg)
20200727 T2 small w playing game [generating function (binomial inversion technique)]

Create a form whose client area is 800 pixels by 600 pixels
![[Oracle database] mammy tutorial day04 Sorting Query](/img/79/9db26aa2d9dbb5514427edf03004f4.png)
[Oracle database] mammy tutorial day04 Sorting Query

C memory alignment
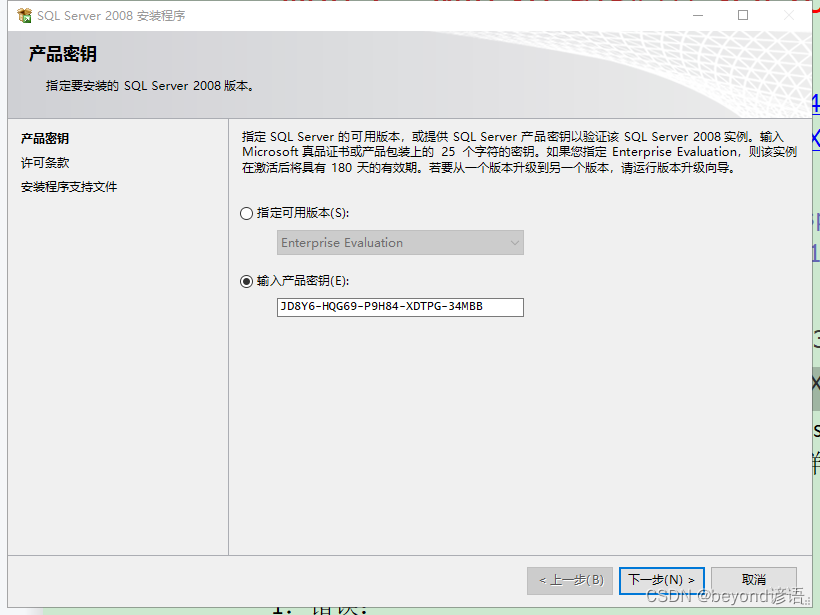
1、 Sqlserver2008 installation (with password), database creation, C form project test

Building a full-featured NAS server with raspberry pie (06): built-in file synchronization tool for penetration
随机推荐
QT table display data
正则表达式匹配
Compound RateModel合约解析
[analysis of STL source code] summary note (4): behind the scenes hero allocator
多线程复习总结之解析Volatile关键字
20200730 T3 small B farm [maximum perimeter empty rectangle (monotone stack + line segment tree)] & "ROI 2017 day 2" learning track
Atomicinteger atomic operation class
[STL source code analysis] summary notes (10): hashtable exploration
Nim product
Aiop introduction
P3327 [sdoi2015] approximate sum (Mobius inversion + formula)
P5431 [template] multiplicative inverse 2
20200727 T2 small w playing game [generating function (binomial inversion technique)]
Leetcode-104. Maximum Depth of Binary Tree
Installation de SQL Server 2008 (avec mot de passe), création d'une base de données, test de projet de formulaire C
[compilation principle] 05- syntax guided semantic computing -- Semantic Computing Based on translation mode
Post-processing of ffmpeg miscellaneous notes
big.js--使用/实例
MySQL设置管理员密码无法生效的案例一则
Building a full-featured NAS server with raspberry pie (05): playing with video and audio & sorting out movies