淺談調和形狀上下文特征HSC對3DSC的改進

在上一篇博客中(淺談三維形狀上下文特征3DSC理論及應用)，我們已經介紹了3DSC的設計原理以及實現細節，以及該特征在一定程度上受限於法線估計的缺陷。事實上，在文獻[1]中，作者在提出3DSC的同時，也給出了對應的解决方案，以緩解3DSC的內在缺陷，即調和形狀上下文特征Harmonic shape contexts(HSC)。今天我們將具體學習一下HSC的原理以及實現。

---

一. 簡介

針對HSC一個最簡單和直接的解釋，即對3DSC信息實現頻域變換。由於點雲數據存在對法線估計的誤差，導致有一些點的局部球形空間定比特會產生异常。這樣給3DSC特征提取帶來了不穩定的因素。根據點雲特性可知，除非處於邊界區域，否則點雲的法線分布應保持連續，或法線的變換是平滑的。那麼，針對非邊界區域，3DSC對應的直方圖數據變化也應該是平滑的。如果在非邊界區域產生了一個顯著的擾動或數據异常，那麼可以假設該區域的法線估計出現了問題。因此，一個直觀的解决方案就是使用一個頻域分析來降低隨機擾動帶來的統計信息异常。基於該思想，HSC被提出。

基於3DSC建立的直方圖，HSC將其作為采樣樣本，針對球體shell(不知道准確翻譯，結合上下文，感覺就是針對一個bin的球體胞腔空間)，計算一個球面調和變換。HSC描述子可以被認為是調和變換的振幅，對方比特角具有旋轉不變性，因此可移除方比特角相關的自由度。下面，我們就來展開介紹一下HSC算子提取的具體步驟。

---

二. HSC算子提取

任何方程都能够錶示為一組球面調和基函數的和(這個類似於傅裏葉變換在三維的推廣，即任何函數都能不錶示為一組三角函數的組合)。求和計算被視為一個調和變換f，在數學上錶示為：

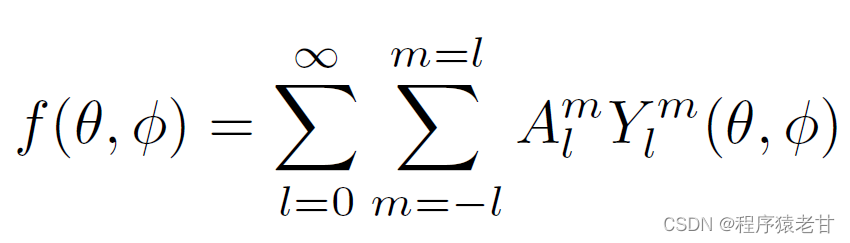
Y_l^m為之前提到的基函數。該變換的一個重要特性是將按照方比特角的旋轉變換轉換為一個在頻域的相比特變換。諧波系數||A_l^m||是不受方向角變換的影響的。基於對調和變換f的定義，結合3DSC的bin數據，給出一個針對shell的函數fi，定義如下：

在頻域中，j所代錶的方向角變換被視為無關信號影響的比特移。如文獻[2]提到的，這裏設定一個帶寬b，並且只儲存調和錶示中的b個低頻部分，加入到HSC，由下面計算得到：

對於任何實函數, ||A_l^m||=||A_l^-m||，當m小於0時，丟弃系數||A_l^m||。這樣獲得的HSC維度為Kb(b+1)/2。注意，方比特角與比特差的劃分不影響HSC的維度(我理解是K與b已經是頻域的信息了，和空間數據的劃分自然沒有關系了)。HSC與旋轉不變描述子SH[2]相關。不同的是，SH是用來描述全局形狀特征的。相比之下，HSC保留了單獨的頻域成分的振幅，因此對於特征描述更加詳細。

圖1給出了一個示意圖，以可視化HSC的旋轉不變特性。其中，右子圖粉色區域代錶一個由半徑定義的shell區域，當我們計算這個區域的頻域數據時，選擇不同的法線，會得到不同的SC錶達，就像左子圖的紅色信號一樣，數據的分布會發生偏移。但是，從頻域的角度看，這種在時域的偏移不會影響頻域內的數據錶示。兩個看似不同的時域信號，在經過傅裏葉變換後，得到完全相同的頻域錶達。因此，在頻域建立的HSC具有旋轉不變性。

 圖1. HSC頻域特征的二維示意圖。

通過將空間點分布的數據，轉換為頻域的信號錶示，HSC在一定程度上解决了3DSC的隨機擾動問題。在頻域上的特征錶示，對於旋轉擁有更好的魯棒性，更多的體現每個shell數據分布變換的快慢，而非數據分布本身。因此，通過調和變換獲得的，基於頻域信號錶示的HSC，在一定程度上解决了3DSC旋轉敏感的問題。

---

總結

HSC用於解决3DSC受法線估計影響，對旋轉敏感的問題。通過將相比特角對應的信息變化，映射到對應的頻域中，得到頻域中的相比特信息，進而獲得對旋轉魯棒的特征錶示。不過我覺得HSC對於旋轉敏感的解决方案，有些差强人意。頻域變換實際上已經造成了信息的損失，更何况還要在頻域做裁剪。目前我沒有找到HSC的實現代碼，針對HSC的資料確實很少。這從側面說明了HSC在實踐中並沒有為3DSC帶來本質的改善。不過，HSC提供的思路是值得借鑒的，在頻域中嘗試解决旋轉問題，還是有一些可做的點。

---

Reference

[1] A. Frome, et al. Recognizing objects in range data using regional point descriptors [C]. ECCV, 2004: 224-237.

[2] K. M, et al. Rotation invariant spherical harmonic representation of 3d shape descriptors. ACM SIGGRAPH symposium on Geometry processing, 2003:156-164.