当前位置:网站首页>P1891 crazy LCM (Euler function)
P1891 crazy LCM (Euler function)
2022-07-03 19:14:00 【It's Alpaca duck】
Topic link : Click here
The main idea of the topic :
seek ∑ i = 1 n l c m ( i , n ) \sum_{i=1}^nlcm(i,n) ∑i=1nlcm(i,n)
Topic analysis :
The same way of thinking Yueyue gives Hua Hua a question
We know l c m ( i , n ) = i ⋅ n gcd ( i , n ) lcm(i,n)=\frac{i·n}{\gcd(i,n)} lcm(i,n)=gcd(i,n)i⋅n
So the question is transformed into ∑ i = 1 n i ⋅ n gcd ( i , n ) = n ⋅ ∑ i = 1 n i gcd ( i , n ) \sum_{i=1}^n\frac{i·n}{\gcd(i,n)}=n·\sum_{i=1}^n\frac{i}{\gcd(i,n)} ∑i=1ngcd(i,n)i⋅n=n⋅∑i=1ngcd(i,n)i
and
∑ i = 1 n i gcd ( i , n ) \sum_{i=1}^n\frac{i}{\gcd(i,n)} i=1∑ngcd(i,n)i
= ∑ d ∣ n 1 d ∑ i = 1 n i [ gcd ( i , n ) = d ] =\sum_{d|n}\frac{1}{d}\sum_{i=1}^n i[\gcd(i,n)=d] =d∣n∑d1i=1∑ni[gcd(i,n)=d]
= ∑ d ∣ n 1 d ∑ i = 1 ⌊ n d ⌋ i d [ gcd ( i , n / d ) = 1 ] =\sum_{d|n}\frac{1}{d}\sum_{i=1}^{\lfloor \frac{n}{d} \rfloor} id[\gcd(i,n/d)=1] =d∣n∑d1i=1∑⌊dn⌋id[gcd(i,n/d)=1]
= ∑ d ∣ n n / d ⋅ φ ( n / d ) + [ n / d = 1 ] 2 =\sum_{d|n}\frac{n/d·\varphi(n/d)+[n/d=1]}{2} =d∣n∑2n/d⋅φ(n/d)+[n/d=1]
= ∑ d ∣ n d ⋅ φ ( d ) + [ d = 1 ] 2 =\sum_{d|n}\frac{d·\varphi(d)+[d=1]}{2} =d∣n∑2d⋅φ(d)+[d=1]
Sift the Euler function in advance , Then, according to the above formula, the time complexity of harmonic series can be used to enumerate the enumeration factors to calculate the contribution
Then finally, for each group of input, use n n n Multiply by the previously calculated value
The overall time complexity is O ( n log n + t ) O(n\log n+t) O(nlogn+t)
See code for details :
// Problem: P1891 insane LCM
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P1891
// Memory Limit: 125 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)
//#pragma GCC optimize(2)
//#pragma GCC optimize("Ofast","inline","-ffast-math")
//#pragma GCC target("avx,sse2,sse3,sse4,mmx")
#include<iostream>
#include<cstdio>
#include<iomanip>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<vector>
#include<set>
#include<map>
#include<stack>
#include<queue>
#define ll long long
#define inf 0x3f3f3f3f
#define Inf 0x3f3f3f3f3f3f3f3f
#define int ll
#define endl '\n'
#define IOS ios::sync_with_stdio(0); cin.tie(0); cout.tie(0)
using namespace std;
int read()
{
int res = 0,flag = 1;
char ch = getchar();
while(ch<'0' || ch>'9')
{
if(ch == '-') flag = -1;
ch = getchar();
}
while(ch>='0' && ch<='9')
{
res = (res<<3)+(res<<1)+(ch^48);//res*10+ch-'0';
ch = getchar();
}
return res*flag;
}
const int maxn = 1e6+5;
const int mod = 1e9+7;
const double pi = acos(-1);
const double eps = 1e-8;
int n,cnt,pri[maxn],phi[maxn],ans[maxn];
bool vis[maxn];
void init(int n)
{
vis[1] = phi[1] = 1;
for(int i = 2;i <= n;i++)
{
if(!vis[i])
{
pri[++cnt] = i;
phi[i] = i-1;
}
for(int j = 1;j<=cnt && i*pri[j]<=n;j++)
{
vis[i*pri[j]] = true;
if(i%pri[j] == 0)
{
phi[i*pri[j]] = phi[i]*pri[j];
break;
}
phi[i*pri[j]] = phi[i]*(pri[j]-1);
}
}
}
signed main()
{
n = maxn-1;
init(n);
for(int i = 1;i <= n;i++)
for(int j = 1;j*i <= n;j++) ans[i*j] += phi[j]*j/2;
// for(int i = 1;i <= n;i++) cout<<ans[i]+1<<endl;
int t = read();
while(t--)
{
n = read();
printf("%lld\n",1LL*n*(ans[n]+1));
}
return 0;
}
边栏推荐
- my. INI file not found
- Random numbers in a long range, is that right- Random number in long range, is this the way?
- EGO Planner代码解析bspline_optimizer部分(2)
- 01. Preparation for automated office (free guidance, only three steps)
- 235. 二叉搜索树的最近公共祖先【lca模板 + 找路径相同】
- Why should the gradient be manually cleared before back propagation in pytorch?
- SQL injection for Web Security (1)
- EGO Planner代码解析bspline_optimizer部分(3)
- Ego planner code parsing Bspline_ Optimizer section (3)
- 【数学建模】基于matlab船舶三自由度MMG模型【含Matlab源码 1925期】
猜你喜欢
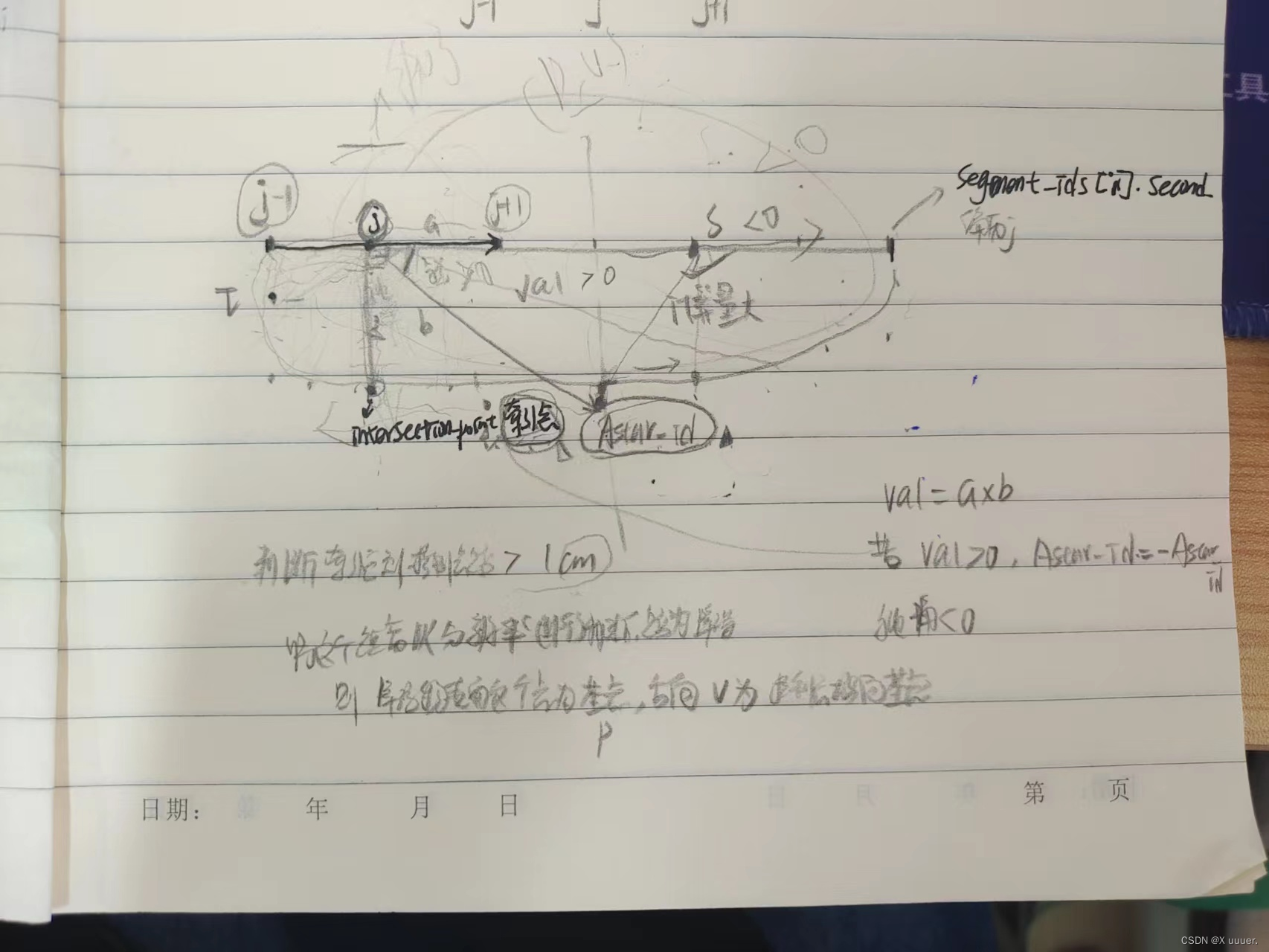
Ego planner code parsing Bspline_ Optimizer section (2)

Zhengda futures news: soaring oil prices may continue to push up global inflation
![Free hand account sharing in September - [cream Nebula]](/img/4f/fec31778a56886585e35be87885452.jpg)
Free hand account sharing in September - [cream Nebula]

The installation path cannot be selected when installing MySQL 8.0.23
【Proteus仿真】用24C04与1602LCD设计的简易加密电子密码锁
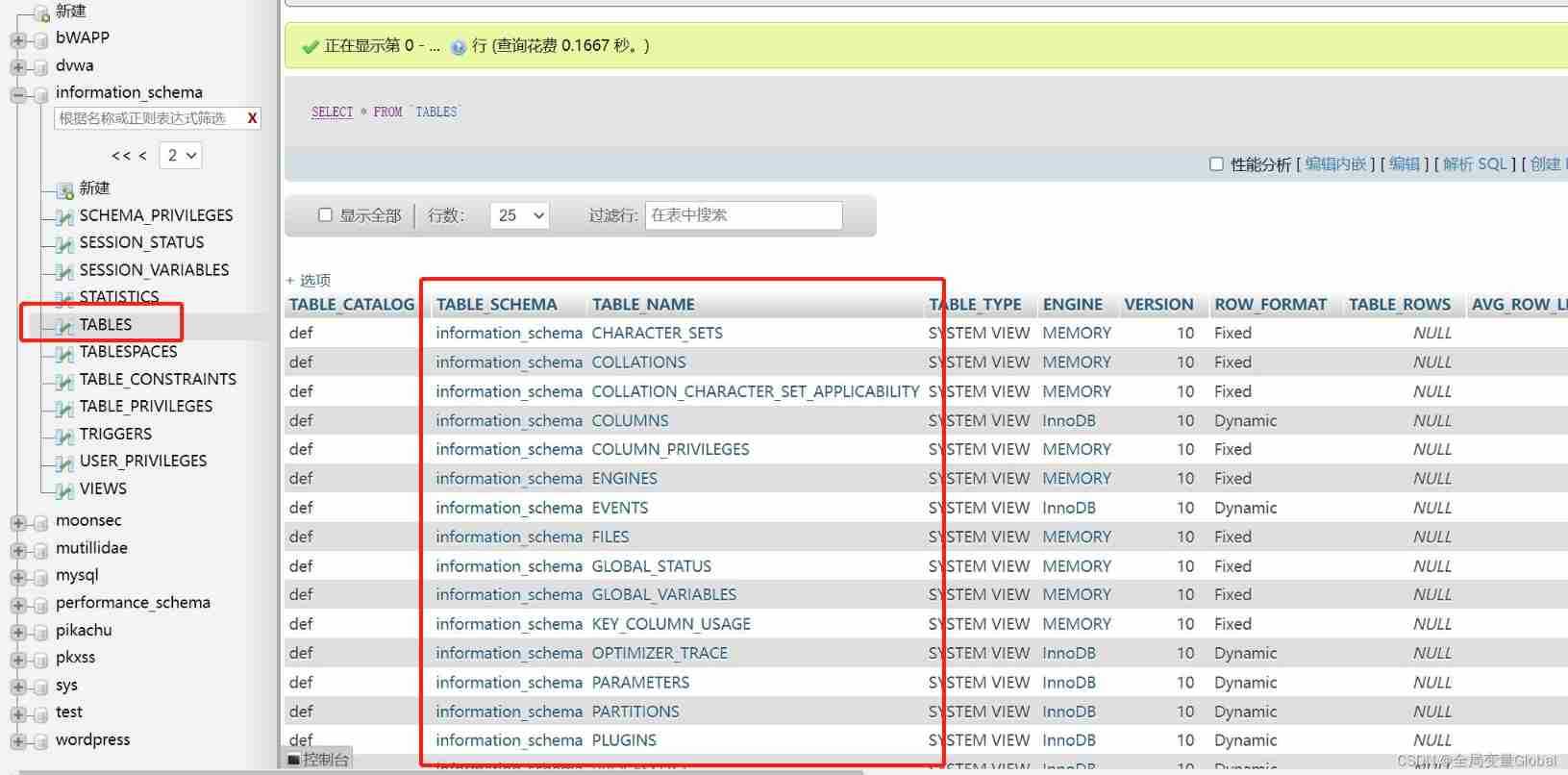
SQL injection for Web Security (1)
![235. The nearest common ancestor of the binary search tree [LCA template + same search path]](/img/f5/f2d244e7f19e9ddeebf070a1d06dce.png)
235. The nearest common ancestor of the binary search tree [LCA template + same search path]
Record: solve the problem that MySQL is not an internal or external command environment variable

OSPF - detailed explanation of stub area and full stub area

Pytorch introduction to deep learning practice notes 13- advanced chapter of cyclic neural network - Classification
随机推荐
[wallpaper] (commercially available) 70 wallpaper HD free
Redis master-slave synchronization, clustering, persistence
Nous avons fait une plateforme intelligente de règlement de détail
These problems should be paid attention to in the production of enterprise promotional videos
HOW TO WRITE A DAILY LAB NOTE?
The necessity of lean production and management in sheet metal industry
Ctrip will implement a 3+2 work system in March, with 3 days on duty and 2 days at home every week
Simple solution of physical backup and restore of Damon database
This Chinese numpy quick look-up table is too easy!
Php based campus lost and found platform (automatic matching push)
EGO Planner代码解析bspline_optimizer部分(2)
Compose LazyColumn 顶部添加控件
TFs and SVN [closed] - TFs vs SVN [closed]
OSPF - detailed explanation of stub area and full stub area
Leetcode: 11. Récipient contenant le plus d'eau [double pointeur + cupidité + enlèvement de la plaque la plus courte]
Understanding of database architecture
Day18 - basis of interface testing
Dart JSON编码器和解码器剖析
Analysis of dart JSON encoder and decoder
The installation path cannot be selected when installing MySQL 8.0.23