当前位置:网站首页>leetcode二叉树系列(二)
leetcode二叉树系列(二)
2022-08-04 09:03:00 【你食不食油饼】
1、二叉树展开为链表
题目描述:

1)暴力拼接
思路:就是遍历每一个节点root,找到当前节点左子树的最右节点pre,
pre.right = root.right
root.right = root.left
root.left = null
这样遍历每一个节点,就可以去掉所有节点的左子树
代码如下:
public void flatten(TreeNode root) {
TreeNode pre;
while (root!=null){
//左子树为空,则跳过
if (root.left == null) {
root = root.right;
} else {
pre = root.left;
//找到当前节点左子树的最右节点
while (pre.right != null) pre = pre.right;
pre.right = root.right;
root.right = root.left;
root.left = null;
root = root.right;
}
}2)先序遍历拼接
思路:根据先序遍历的顺序依次,把左子树拼接到右子树
代码如下:
TreeNode pre;
public void flatten(TreeNode root) {
if(root == null) return;
TreeNode left = root.left;
TreeNode right = root.right;
root.left = null;
if(pre != null) pre.right = root;
pre = root;
flatten(left);
flatten(right);
}3)后序遍历拼接(变种)
思路:于先序遍历完全相反,由右子树最右节点开始,依次拼接
代码:
TreeNode last;
public void flatten(TreeNode root) {
if (root == null ) return;
flatten(root.right);
flatten(root.left);
//pre表示最后一个节点,依次往上建立
root.right = last;
root.left = null;
last = root;
}总结:这道题万变不离其宗,根据先序遍历的顺序,把左子树拼接到右子树,了解这点就很简单
2、二叉树中的最大路径和
题目描述:


思路:题目是要我们求最大路径和,规定路径的节点只能出现一次
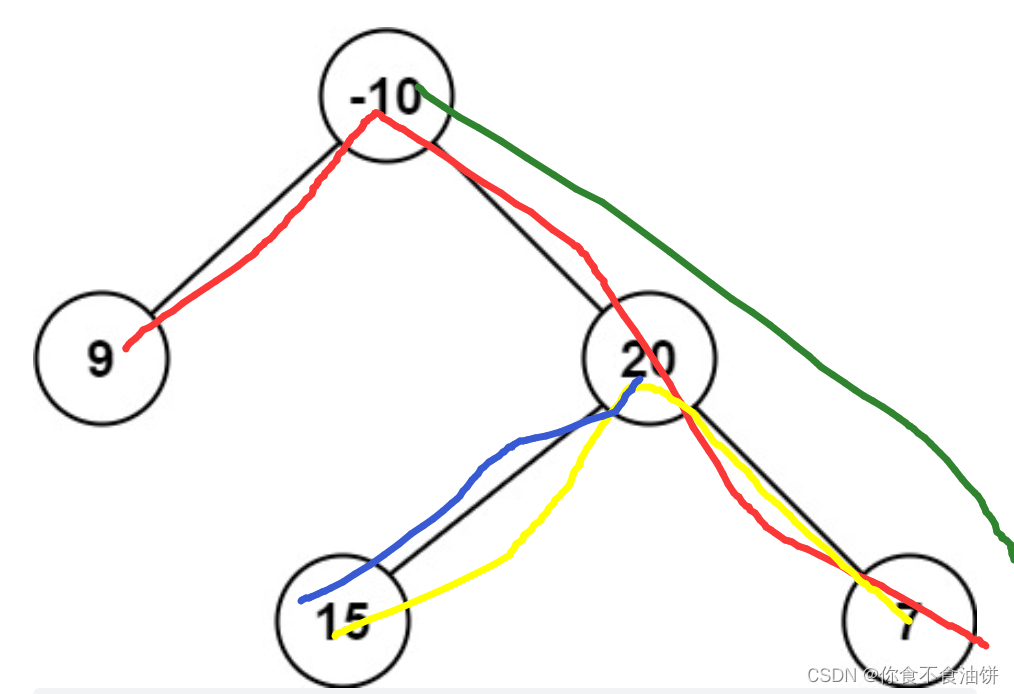
如图路径一般有四种情况
- 我自己就是一条路径
- 只跟左子节点合并成一条路径
- 只跟右子节点合并成一条路径
- 以自己为桥梁,跟左、右子节点合并成一条路径
我们就需要用到递归,求出每一个结点的2、3情况,并返回较大的路径和
同时,在每次递归时,都需要不断进行最大路径和的判断,因为我们不知道在哪个节点时会取到最大路径和!
进入代码:
int max = Integer.MIN_VALUE;
public int maxPathSum(TreeNode root) {
dfs(root);
return max;
}
public int dfs(TreeNode root){
if (root == null) return 0;
//由于路径加起来可能是负的,所以做一个比较
int leftPath = Math.max(0,dfs(root.left));
int rightPath = Math.max(0,dfs(root.right));
max = Math.max(max,root.val + leftPath + rightPath);
//返回左边路径和或者右边路径和的较大值
return root.val + Math.max(leftPath,rightPath);
}持续更新中~~
边栏推荐
猜你喜欢

张朝阳对话俞敏洪:谈宇宙、谈焦虑、谈创业、谈退休、谈人生
recursive thinking
94后字节P7晒出工资单:狠补了这个,真不错...
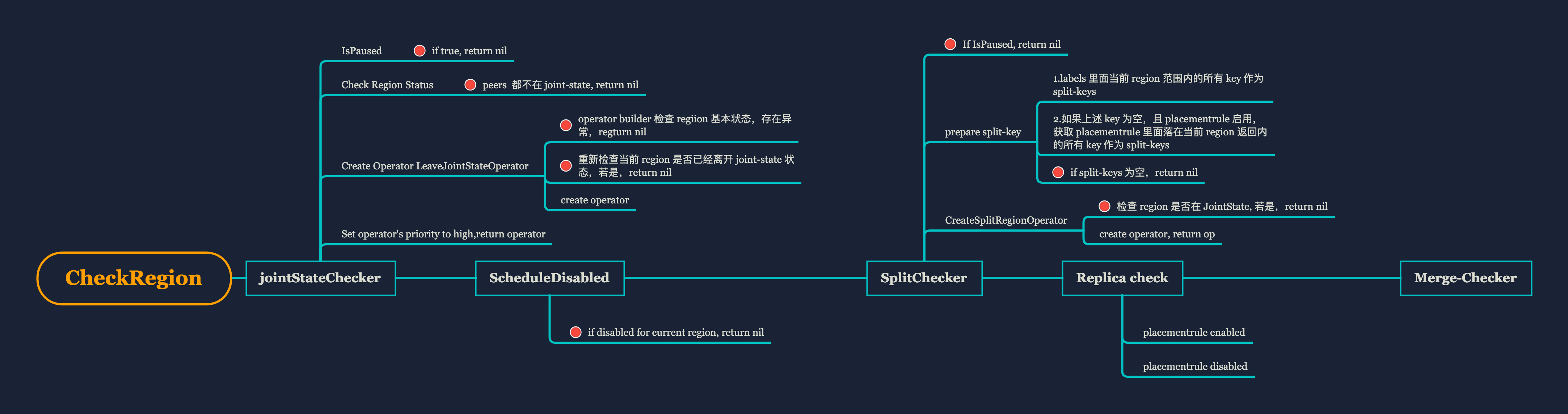
PD 源码分析- Checker: region 健康卫士
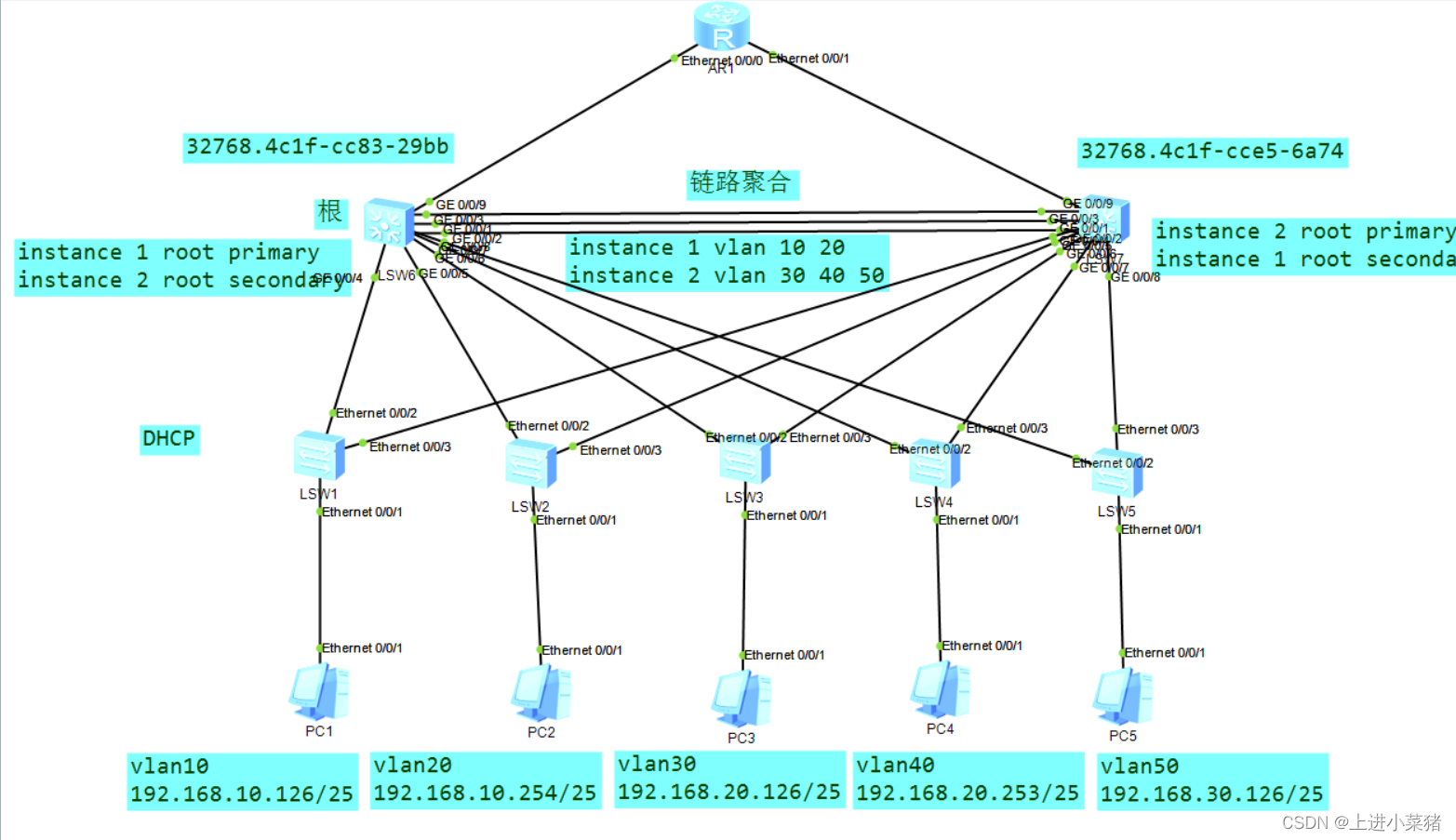
三层交换机配置MSTP协议详解【华为eNSP实验】
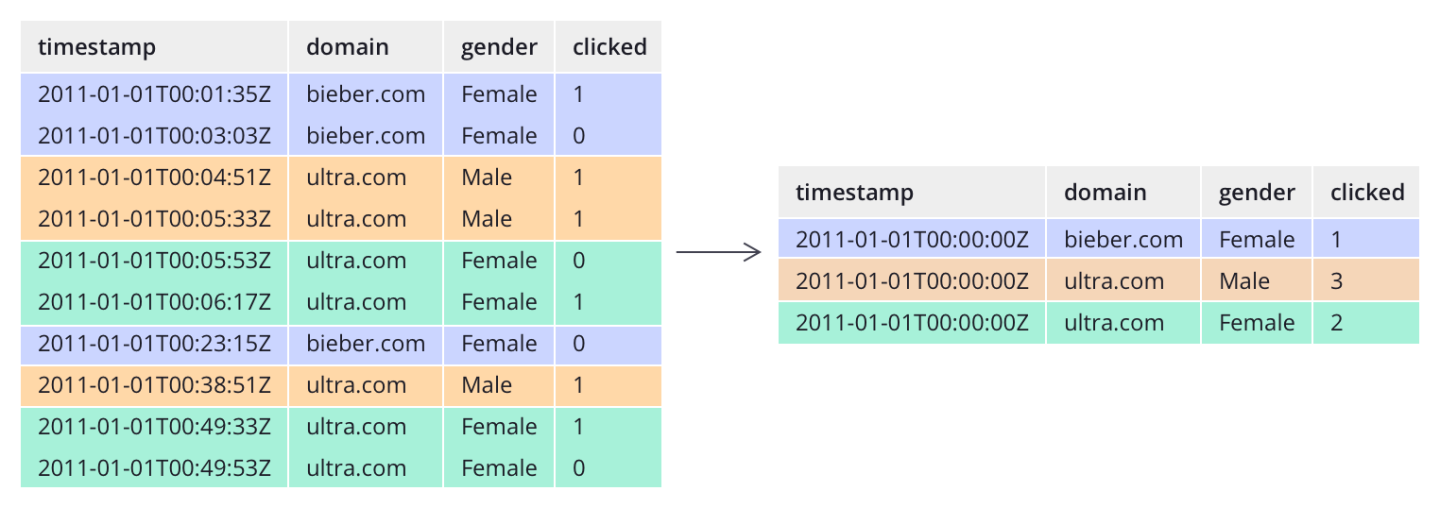
Apache Druid 实时分析数据库入门介绍

Anton Paar Anton Paar Density Meter Hydrometer Repair DMA35 Performance Parameters
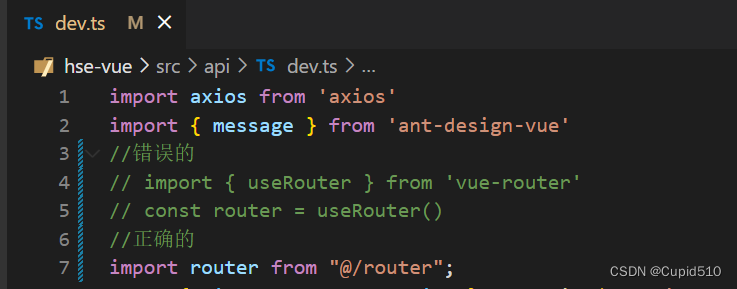
inject() can only be used inside setup() or functional components.
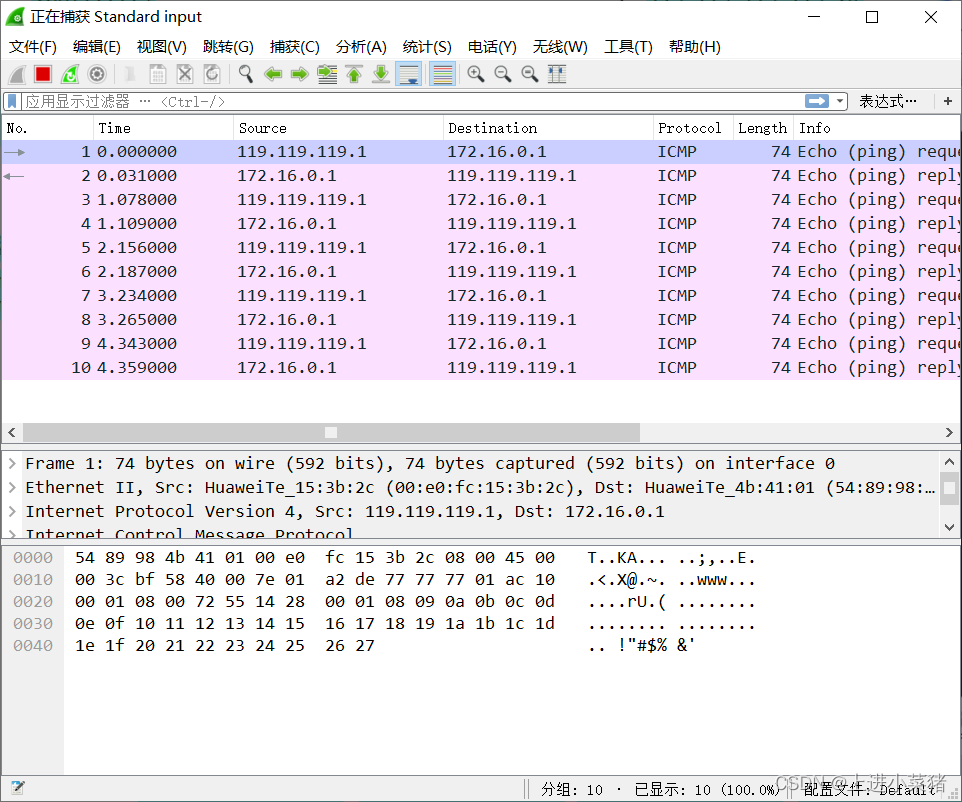
NAT/NAPT地址转换(内外网通信)技术详解【华为eNSP】
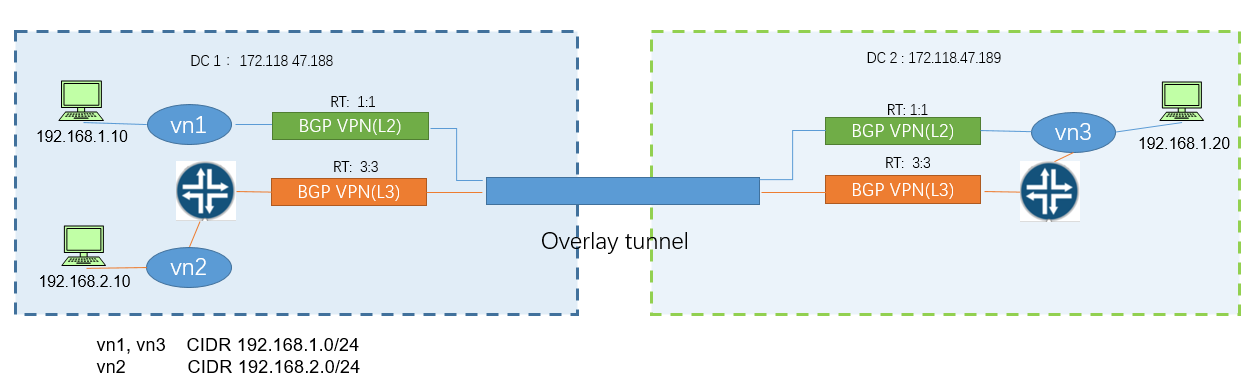
智汇华云 | 华云软件定义网络 DCI介绍
随机推荐
yuv420sp转jpg
After four years of outsourcing, the autumn recruits finally landed
Interview at 14:00 in the afternoon, I came out at 14:08 with my head down, asking too much...
预测性维护学习之路
布局管理器
2022-08-02 Analyze RK817 output 32k clock PMIC_32KOUT_WIFI to WiFi module clock register devm_clk_hw_register
Shared_preload_libraries cause many syntaxes not supported
js - the first letter that appears twice
Interpretation of new features | MySQL 8.0 online adjustment REDO
技术实现 | 图像检索及其在高德的应用
2022-08-02 分析RK817 输出32k clock PMIC_32KOUT_WIFI给WiFi模块 clock 注册devm_clk_hw_register
BFM模型和Landmarks可视化
ansible部署脚本--亲测可用无坑
Convert callback function to Flow
继承和static关键字
王爽汇编语言第四章:第一个程序
Could you please talk about how the website is accessed?[Interview questions in the web field]
The separation configuration Libpq is supported, speaking, reading and writing
他97年的,我既然卷不过他...
GBsae 8c 数据库使用中报错,肿么办?