AcWing 245. Can you answer these questions (line segment tree)

The segment tree is so easy to make segment errors .. Simply call it line segment error tree ！

If you want to review the line segment tree , Poke this ： Line segment tree blue book explanation

The question ：

Ideas ：

This question is based on the meaning of the question Single point modification , Therefore, there is no need to mark pushdown operation , It only needs pushup Just operate .

For the maximum sub segment and , We need to think about what information needs to be stored inside each node .

Set the node in the segment tree as “node”, We obviously The left side of the interval should be stored first 、 Right endpoint ：l、r, Because the segment tree is essentially a binary tree with intervals as nodes .

meanwhile , According to the meaning of the title It should also store the largest continuous sub segment and , We use it total_max Express , Shorthand for tmax.

Let's think about it , Is it enough to store only this information ？ Use only the currently stored information , Can achieve The maximum continuous sub segment sum of the parent node tmax from The sum of the largest continuous sub segments of the two child nodes Find it ？

Obviously not enough .

reason ： Two Son node Their respective tmax There may be Completely inside the interval The situation of , And No boundaries , However Father node Of tmax There may be “ Across two intervals The situation of ”. As shown in the figure below （ The range contained in red brackets indicates the tmax）：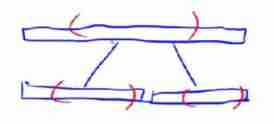

For this kind of “ Parent node tmax Across two intervals ” In this case , We actually need to Store two additional messages ：

• ① Take the right end of the left son interval as the starting point towards the left The maximum suffix of and .

• ② Take the left end point of the right son interval as the starting point towards the right The maximum prefix and .

To sum up , That is, each node also needs to store its The maximum prefix and and Maximum suffix and , such , Parent node “ Across two sections ” The largest continuous subsegment and be equal to The maximum suffix of the left son and add The maximum prefix of the right son and .

（ The range of left and right sons is completely independent , There is no relationship between the two , There is no limit to , The left and right intervals take max That is, the parent node tmax）

We set nodes The maximum prefix and by lmax, Maximum suffix and by rmax.

We have the following Three situations ：

Parent node tmax There is no span There are two situations ：

• ① Completely inside the left son section ：tmax = Left son tmax

• ② Completely inside the right son section ：tmax = Right son tmax

Parent node tmax Across two sections The situation is one ：

• ③tmax = Left son rmax + Right son lmax

Synthesize to get the expression ：

Parent node u.tmax = max{L_son.tmax, R_son.tmax, L_son.rmax + R_son.lmax}

thus , We have a method to calculate the tmax 了 .

But we still need to think about the two new variables ：lmax（ The maximum prefix and ） and rmax（ Maximum suffix and ） How to get .

It is similar to the previous way of thinking , Let's discuss it according to the situation ：

For one Parent node Of lmax, We can also be divided into Two cases ：

• ① There is no crossing point , Here's the picture , Parent node lmax = Left son lmax.
  
• ② Crossed the dividing point , Here's the picture .
  

For the case above ②, We find it impossible to use the existing conditions , The maximum prefix sum of the parent node lmax be equal to Sum of left son intervals add Right son lmax.

Empathy , The maximum suffix sum of the parent node rmax be equal to Sum of right son intervals add Left son rmax.

So , Our node finally needs a new information ： Interval and （ Set to sum）

And for Parent node sum It can also be calculated , We can Left son sum add Right son sum,
expression ： Parent node u.sum = L_son.sum + R_son.sum

We get two conclusions about Maximum prefix and The expression of ：

• ① Parent node u.lmax = max{L_son.lmax, L_son.sum + R_son.lmax}

• ② Parent node u.rmax = max{R_son.rmax, R_son.sum + L_son.rmax}

thus , We have been able to confirm What variables are contained in the structure storing the segment tree , Then we can determine pushup Function writing , The whole coding The general framework remains unchanged , from Four functions constitute ：pushup From son to father Transmit information 、build establish 、modify modify 、ask Inquire about .

Time complexity ：

O(mlogn)（m<=1e5,n<=5e5）

Code ：

#include<bits/stdc++.h>

using namespace std;

const int N = 5e5+10;
int a[N];
int n, m;
struct node
{
        int l, r;
        int tmax;
        int sum;
        int lmax, rmax;
} t[N<<2];

void pushup(node &u, node &l, node &r)
{
        u.sum = l.sum + r.sum;
        u.tmax = max(max(l.tmax, r.tmax), l.rmax+r.lmax);
        u.lmax = max(l.lmax, l.sum+r.lmax);
        u.rmax = max(r.rmax, r.sum+l.rmax);
}

void pushup(int u){
        pushup(t[u], t[u<<1], t[u<<1|1]);
}

void build(int u, int l, int r)
{
        t[u].l = l, t[u].r = r;
        if(l==r) { t[u].tmax = t[u].sum = t[u].lmax = t[u].rmax = a[l]; return ; }

        int mid = l+r>>1;
        build(u<<1, l, mid), build(u<<1|1, mid+1, r);
        pushup(u);
}

void modify(int u, int x, int v)
{
        if(t[u].l==t[u].r) { t[u] = {x, x, v, v, v, v}; return ;}
        int mid = t[u].l+t[u].r>>1;
        if(x<=mid) modify(u<<1, x, v);
        else modify(u<<1|1, x, v);
        pushup(u);
}

node ask(int u, int l, int r)
{
        if(l<=t[u].l&&r>=t[u].r) return t[u];

        int mid = t[u].l+t[u].r>>1;
        if(r<=mid) return ask(u<<1, l, r);
        else if(l>=mid+1) return ask(u<<1|1, l, r);
        else
        {
                auto left = ask(u<<1, l, r);
                auto right = ask(u<<1|1, l, r);
                node res;
                pushup(res, left, right);
                return res;
        }
}

int main()
{
        scanf("%d%d", &n, &m);
        for(int i=1;i<=n;++i) scanf("%d", &a[i]);

        build(1, 1, n);
        while(m--)
        {
                int k, x, y;
                scanf("%d%d%d", &k, &x, &y);

                if(k==1)
                {
                        if(x>y) swap(x, y);
                        printf("%d\n", ask(1, x, y).tmax);
                }
                else
                {
                        modify(1, x, y);
                }
        }


        return 0;
}