当前位置:网站首页>Detailed analysis of pytorch's automatic derivation mechanism, pytorch's core magic
Detailed analysis of pytorch's automatic derivation mechanism, pytorch's core magic
2022-07-04 14:26:00 【Xiaobai learns vision】
Click on the above “ Xiaobai studies vision ”, Optional plus " Star standard " or “ Roof placement ”
Heavy dry goods , First time delivery author :Vaibhav Kumar
compile :ronghuaiyang
Reading guide
This article analyzes in detail PyTorch Automatic derivation mechanism , Let you know PyTorch Core magic of .

We all agree that , When it comes to large neural networks , We are not good at calculus . It is unrealistic to calculate the gradient of such a large composite function by explicitly solving mathematical equations , In particular, these curves exist in a large number of dimensions , It's incomprehensible .
To deal with 14 Hyperplane in dimensional space , Imagine a three-dimensional space , Say to yourself loudly “14”. Everyone does this ——Geoffrey Hinton
This is it. PyTorch Of autograd Where it works . It abstracts complex mathematics , Help us “ Miraculously ” Calculate the gradient of high-dimensional curve , Just a few lines of code . This article attempts to describe autograd The magic of .
PyTorch Basics
Before further discussion , We need to know some basic PyTorch Concept .
tensor : In short , It's just PyTorch One of them n Dimension group . Tensors support some additional enhancements , This makes them unique : except CPU, They can be loaded or GPU Faster computing . Set up .requires_grad = True When , They began to form a reverse diagram , Tracking is applied to each of their operations , Use the so-called dynamic calculation diagram (DCG) Calculate the gradient ( It will be explained further later ).
In earlier versions PyTorch in , Use torch.autograd.Variable Class is used to create tensors that support gradient computation and operation tracking , But up to PyTorch v0.4.0,Variable Class is disabled .torch.Tensor and torch.autograd.Variable Now it is the same class . More precisely , torch.Tensor Be able to track history and behave like the old Variable.
import torch
import numpy as np
x = torch.randn(2, 2, requires_grad = True)
# From numpy
x = np.array([1., 2., 3.]) #Only Tensors of floating point dtype can require gradients
x = torch.from_numpy(x)
# Now enable gradient
x.requires_grad_(True)
# _ above makes the change in-place (its a common pytorch thing)Be careful : according to PyTorch The design of the , Gradients can only compute floating-point tensors , This is why I created a floating point type numpy Array , Then set it to gradient enabled PyTorch tensor .
Autograd: This class is an engine for calculating derivatives ( More precisely, Jacobian vector product ). It records a graph of all operations on the gradient tensor , And create an acyclic graph called dynamic calculation graph . The leaf nodes of this graph are input tensors , The root node is the output tensor . The gradient is achieved by tracing the graph from root to leaf , And use the chain rule to multiply each gradient .
Neural networks and back propagation
Neural networks are only carefully tuned ( Training ) A compound mathematical function that outputs the desired result . Adjustment or training is done through an excellent algorithm called back propagation . Back propagation is used to calculate the loss gradient relative to the input weight , So that the weight can be updated later , Ultimately reduce losses .
In a way , Back propagation is just a fancy name for the chain rule —— Jeremy Howard
Creating and training neural networks includes the following basic steps :
Define the architecture
Use input data to propagate forward architecturally
Calculate the loss
Back propagation , Calculate the gradient of each weight
Update weights with learning rates
The small change of the input weight caused by the loss change is called the gradient of the weight , And use back propagation to calculate . Then use the gradient to update the weight , Use the learning rate to reduce the loss as a whole and train the neural network .
This is done iteratively . For each iteration , You have to calculate several gradients , And build something called a computational graph for storing these gradient functions .PyTorch By building a dynamic calculation diagram (DCG) To achieve this . This diagram is built from scratch in each iteration , It provides maximum flexibility for gradient calculation . for example , For forward operation ( function )Mul , Backward operation function MulBackward It is dynamically integrated into the backward graph to calculate the gradient .
Dynamic calculation diagram
Tensors that support gradients ( Variable ) And the function ( operation ) Combine to create a dynamic calculation diagram . Data flows and operations applied to data are defined at run time , So as to dynamically construct the calculation diagram . This diagram is composed of the bottom autograd Class dynamically generated . You don't have to code all possible paths before starting training —— What you run is what you distinguish .
A simple DCG The multiplication for two tensors would be like this :
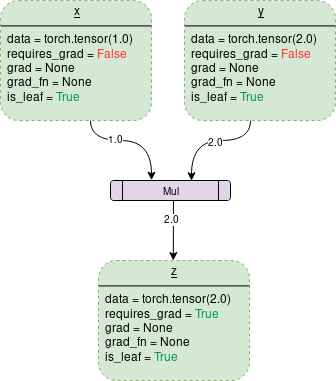
Each point outline box in the figure is a variable , The purple rectangle is an operation .
Each variable object has several members , Some of the members are :
Data: It is the data held by a variable .x Hold one 1x1 tensor , Its value is equal to 1.0, and y hold 2.0.z Hold the product of two , namely 2.0.
requires_grad: This member ( If true) Start tracking all operation history , And form a backward graph for gradient calculation . For any tensor a, It can be treated in situ as follows :a.requires_grad_(True).
grad: grad Save the gradient value . If requires_grad by False, It will hold a None value . Even if requires_grad It's true , It will also hold a None value , Unless called from another node .backward() function . for example , If you are right about out About x Calculate the gradient , call out.backward(), be x.grad The value of is ∂out/∂x.
grad_fn: This is the backward function used to calculate the gradient .
is_leaf: If :
It is explicitly initialized by some functions , such as
x = torch.tensor(1.0)orx = torch.randn(1, 1)( Basically, all tensor initialization methods discussed at the beginning of this paper ).It is created after the operation of tensor , All tensors have
requires_grad = False.It is by calling
.detach()Method to create .
Calling backward() when , Only calculate requires_grad and is_leaf At the same time, the gradient of true nodes .
When open requires_grad = True when ,PyTorch The tracking operation will begin , And store the gradient function in each step , As shown below :
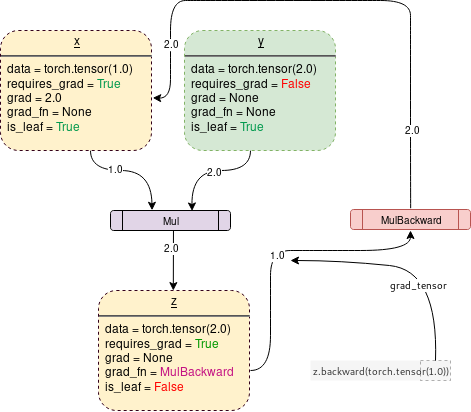
stay PyTorch The code that generates the above figure is :
Backward() function
Backward Functions actually pass parameters ( By default 1x1 Unit tensor ) To calculate the gradient , It passes through Backward The graph goes all the way to each leaf node , Each leaf node can be traced from the root tensor of the call to the leaf node . Then the calculated gradient is stored in the .grad in . please remember , The backward graph has been dynamically generated in the forward transfer process .backward The function calculates the gradient using only the generated graph , And store it in the leaf node .
Let's analyze the following code :
import torch
# Creating the graph
x = torch.tensor(1.0, requires_grad = True)
z = x ** 3
z.backward() #Computes the gradient
print(x.grad.data) #Prints '3' which is dz/dx An important thing to pay attention to is , When calling z.backward() when , A tensor is automatically passed as z.backward(torch.tensor(1.0)).torch.tensor(1.0) Is the external gradient used to terminate the chain rule gradient multiplication . This external gradient is passed as input to MulBackward function , To further calculate x Gradient of . Pass on to .backward() The dimension of the tensor in must be the same as that of the tensor in which the gradient is being calculated . for example , If the gradient supports tensor x and y as follows :
x = torch.tensor([0.0, 2.0, 8.0], requires_grad = True)
y = torch.tensor([5.0 , 1.0 , 7.0], requires_grad = True)
z = x * y then , To calculate z About x perhaps y Gradient of , You need to pass an external gradient to z.backward() function , As shown below :
z.backward(torch.FloatTensor([1.0, 1.0, 1.0])z.backward() Will give RuntimeError: grad can be implicitly created only for scalar outputs
The tensor passed by the inverse function is like the weight of the gradient weighted output . Mathematically speaking , This is a vector multiplied by a non scalar tensor Jacobian matrix ( This paper will further discuss ), Therefore, it is almost always a unit tensor of one dimension , And backward Same tensor , Unless you need to calculate the weighted output .
tldr : The backward graph is composed of autograd Class is automatically and dynamically created during forward passing .
Backward()The gradient is calculated simply by passing its parameters to the generated inverse graph .
mathematics — Jacobian matrix and vector
Mathematically speaking ,autograd Class is just a Jacobian vector product calculation engine . Jacobian matrix is a very simple word , It represents all possible partial derivatives of two vectors . It's the gradient of one vector relative to another .
Be careful : In the process ,PyTorch The entire Jacobian matrix is never explicitly constructed . Direct calculation JVP (Jacobian vector product) It's usually simpler 、 More effective .
If a vector X = [x1, x2,…xn] adopt f(X) = [f1, f2,…fn] To calculate other vectors , Then Jacobian matrix (J) Contains all of the following partial derivative combinations :
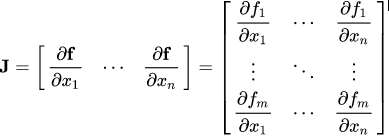
The matrix above represents f(X) be relative to X Gradient of .
Suppose one is enabled PyTorch Tensor of gradient X:
X = [x1,x2,…,xn]( Suppose this is the weight of a machine learning model )
X After some operations, form a vector Y
Y = f(X) = [y1, y2,…,ym]
And then use Y Calculate scalar loss l. Suppose that the vector v It happens to be a scalar loss l About vectors Y Gradient of , as follows :
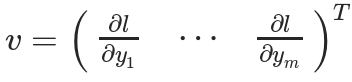
vector v be called grad_tensor, And pass it as a parameter to backward() function .
In order to get the gradient of loss l About weight X Gradient of , Jacobian matrix J Is vector times vector v
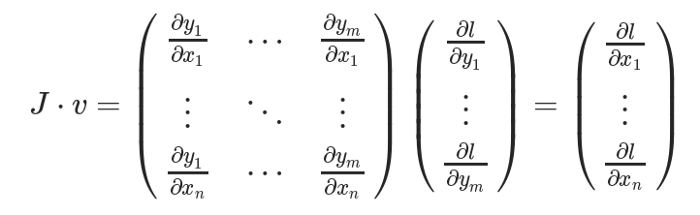
This method calculates the Jacobian matrix and compares it with the vector v The method of multiplication makes PyTorch It can easily provide external gradients for non scalar output .
The good news !
Xiaobai learns visual knowledge about the planet
Open to the outside world

download 1:OpenCV-Contrib Chinese version of extension module
stay 「 Xiaobai studies vision 」 Official account back office reply : Extension module Chinese course , You can download the first copy of the whole network OpenCV Extension module tutorial Chinese version , Cover expansion module installation 、SFM Algorithm 、 Stereo vision 、 Target tracking 、 Biological vision 、 Super resolution processing and other more than 20 chapters .
download 2:Python Visual combat project 52 speak
stay 「 Xiaobai studies vision 」 Official account back office reply :Python Visual combat project , You can download, including image segmentation 、 Mask detection 、 Lane line detection 、 Vehicle count 、 Add Eyeliner 、 License plate recognition 、 Character recognition 、 Emotional tests 、 Text content extraction 、 Face recognition, etc 31 A visual combat project , Help fast school computer vision .
download 3:OpenCV Actual project 20 speak
stay 「 Xiaobai studies vision 」 Official account back office reply :OpenCV Actual project 20 speak , You can download the 20 Based on OpenCV Realization 20 A real project , Realization OpenCV Learn advanced .
Communication group
Welcome to join the official account reader group to communicate with your colleagues , There are SLAM、 3 d visual 、 sensor 、 Autopilot 、 Computational photography 、 testing 、 Division 、 distinguish 、 Medical imaging 、GAN、 Wechat groups such as algorithm competition ( It will be subdivided gradually in the future ), Please scan the following micro signal clustering , remarks :” nickname + School / company + Research direction “, for example :” Zhang San + Shanghai Jiaotong University + Vision SLAM“. Please note... According to the format , Otherwise, it will not pass . After successful addition, they will be invited to relevant wechat groups according to the research direction . Please do not send ads in the group , Or you'll be invited out , Thanks for your understanding ~边栏推荐
猜你喜欢
【FAQ】華為帳號服務報錯 907135701的常見原因總結和解决方法

STM32F1与STM32CubeIDE编程实例-MAX7219驱动8位7段数码管(基于GPIO)
Leetcode 61: rotating linked list
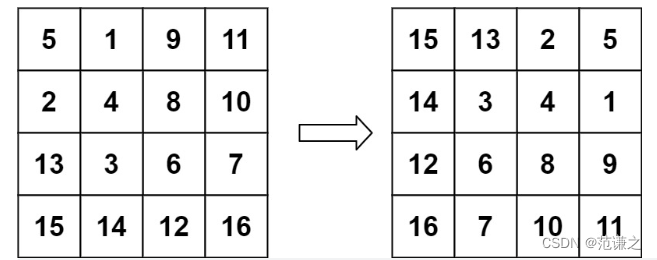
Leetcode T48:旋转图像
聊聊保证线程安全的 10 个小技巧
RK1126平台OSD的实现支持颜色半透明度多通道支持中文

sql优化之explain

scratch古堡历险记 电子学会图形化编程scratch等级考试三级真题和答案解析2022年6月
WT588F02B-8S(C006_03)单芯片语音ic方案为智能门铃设计降本增效赋能
实战解惑 | OpenCV中如何提取不规则ROI区域
随机推荐
Innovation and development of independent industrial software
R language uses dplyr package group_ The by function and the summarize function calculate the mean and standard deviation of the target variables based on the grouped variables
Opencv3.2 and opencv2.4 installation
卷积神经网络经典论文集合(深度学习分类篇)
Leetcode T48:旋转图像
Use of tiledlayout function in MATLAB
R language ggplot2 visualization: gganimate package creates animated graph (GIF) and uses anim_ The save function saves the GIF visual animation
SqlServer函数,存储过程的创建和使用
C # WPF realizes the real-time screen capture function of screen capture box
数据湖(十三):Spark与Iceberg整合DDL操作
Data center concept
迅为IMX6Q开发板QT系统移植tinyplay
实战解惑 | OpenCV中如何提取不规则ROI区域
What is the difference between Bi financial analysis in a narrow sense and financial analysis in a broad sense?
Leetcode t47: full arrangement II
架构方面的进步
R language uses bwplot function in lattice package to visualize box plot and par Settings parameter custom theme mode
Ml: introduction, principle, use method and detailed introduction of classic cases of snap value
Nowcoder rearrange linked list
Nowcoder reverse linked list