当前位置:网站首页>Hidden Markov model (HMM): model parameter estimation
Hidden Markov model (HMM): model parameter estimation
2022-07-01 16:53:00 【HadesZ~】
It is estimated that HMM Model parameters , According to whether the observation sequence corresponds to the state sequence , It can be divided into supervised learning algorithm and unsupervised learning algorithm .
1. Supervised learning estimation HMM Model parameters
Suppose the given training data contains n n n Observation sequence and corresponding state sequence ( The length of different observation sequences can be the same , It can be different ) { ( X 1 , Y 1 ) , ( X 2 , Y 2 ) , ⋯ , ( X n , Y n ) } \{(X_1, Y_1), (X_2, Y_2), \cdots, (X_n, Y_n)\} { (X1,Y1),(X2,Y2),⋯,(Xn,Yn)}, When the state and hang test sequence are known , The model parameter values on each sample can be obtained by direct statistics according to the definition of model parameters , Then the estimation of model parameters can be obtained by calculating the expectation on all samples of the whole training data set .
1.1 Transfer probability a i j a_{ij} aij Estimation
Set the first k k k Among samples , t t t Always in the State s i s_i si、 t + 1 t+1 t+1 Always in the State s j s_j sj The frequency of is A i j A_{ij} Aij, So the state transition probability a i j a_{ij} aij My estimate is :
a ^ i j = ∑ k = 1 n A i j ∑ k = 1 n ∑ j = 1 N A i j , i = 1 , 2 , ⋯ , N ; j = 1 , 2 , ⋯ , N (1.1) \hat{a}_{ij} = \frac{ \sum_{k=1}^{n} A_{ij} }{ \sum_{k=1}^{n} \sum_{j=1}^{N} A_{ij} }, \ \ \ \ \ \ i = 1, 2, \cdots, N; \ \ \ \ j = 1, 2, \cdots, N \tag{1.1} a^ij=∑k=1n∑j=1NAij∑k=1nAij, i=1,2,⋯,N; j=1,2,⋯,N(1.1)
1.2 Observed probability of occurrence b j ( v l ) b_j(v_l) bj(vl) Estimation
Set the first k k k Among samples , Status as s j s_j sj And the observation is o l o_l ol The frequency of this is B j l B_{jl} Bjl, Then the observed probability of occurrence b j ( v l ) b_j(v_l) bj(vl) My estimate is :
b ^ j ( o l ) = ∑ k = 1 n B j l ∑ k = 1 n ∑ l = 1 M B j l , i = 1 , 2 , ⋯ , N ; l = 1 , 2 , ⋯ , M (1.2) \hat{b}_{j}(o_l) = \frac{ \sum_{k=1}^{n} B_{jl} }{ \sum_{k=1}^{n} \sum_{l=1}^{M} B_{jl} }, \ \ \ \ \ \ i = 1, 2, \cdots, N; \ \ \ \ l = 1, 2, \cdots, M \tag{1.2} b^j(ol)=∑k=1n∑l=1MBjl∑k=1nBjl, i=1,2,⋯,N; l=1,2,⋯,M(1.2)
1.3 Initial state probability π i \pi_i πi Estimation
Initial state probability π i \pi_i πi My estimate is n n n Among samples , The frequency of the corresponding state :
π ^ i = 1 n ∑ k = 1 n i f ( y 1 = s i , 1 , 0 ) , i = 1 , 2 , ⋯ , N (1.3) \hat{\pi}_i = \frac{1}{n}\sum_{k=1}^{n}\ if(y_1 = s_i, \ 1, \ 0), \ \ \ \ \ \ i = 1, 2, \cdots, N \tag{1.3} π^i=n1k=1∑n if(y1=si, 1, 0), i=1,2,⋯,N(1.3)
2. Unsupervised learning estimation HMM Model parameters
Because the cost of status tagging is high , So only the observation sequence data is given 、 Request estimate HMM Model parameters are more common . Assume that the training data only contains a length of T T T The sequence of observations X X X And there's no corresponding state sequence Y Y Y, The goal is to estimate the parameters of hidden Markov model λ = ( A , B , π ) \lambda = (A, B, \pi) λ=(A,B,π). In this case , Sequence of States Y Y Y Is an unobservable hidden variable (hidden variable),HHM The model is a probability model with hidden variables :
P ( X ∣ λ ) = ∑ Y P ( X , Y ∣ λ ) = ∑ Y P ( X ∣ Y , λ ) P ( Y ∣ λ ) (2.1) P(X | \lambda)= \sum_{Y}P(X, Y | \lambda) = \sum_{Y}P(X | Y, \lambda)P(Y | \lambda) \tag{2.1} P(X∣λ)=Y∑P(X,Y∣λ)=Y∑P(X∣Y,λ)P(Y∣λ)(2.1) according to EM Algorithm ,HHM The maximum likelihood estimation of model parameters is 1:
λ ^ = arg max λ Q ( λ , λ ˉ ) (2.2) \hat{\lambda} = \argmax_{\lambda} Q(\lambda, \bar{\lambda}) \tag{2.2} λ^=λargmaxQ(λ,λˉ)(2.2) Q ( λ , λ ˉ ) = ∑ Y P ( X , Y ∣ λ ˉ ) ⋅ l o g P ( X , Y ∣ λ ) (2.3) Q(\lambda, \bar{\lambda}) = \sum_{Y} P(X, Y | \bar{\lambda}) \cdot logP(X, Y | \lambda) \tag{2.3} Q(λ,λˉ)=Y∑P(X,Y∣λˉ)⋅logP(X,Y∣λ)(2.3)
according to Q Q Q Function definition , type ( 2.3 ) type (2.3) type (2.3) Omitted λ \lambda λ The constant factor of 1 / P ( X ∣ λ ) 1/P(X | \lambda) 1/P(X∣λ).
Because by definition ,HMM In the model
P ( X , Y ∣ λ ) = π i 1 b i 1 ( x 1 ) ⋅ a i 1 i 2 b i 2 ( x 2 ) ⋯ a i T − 1 i T b i T ( x T ) P(X, Y | \lambda) = \pi_{i_1}b_{i_1}(x_1) \cdot a_{i_1i_2}b_{i_2}(x_2) \cdots a_{i_{T-1}i_T}b_{i_T}(x_T) P(X,Y∣λ)=πi1bi1(x1)⋅ai1i2bi2(x2)⋯aiT−1iTbiT(xT)
So the algorithm based on logarithm , The subitems involved in each parameter of the model in parameter estimation can be disassembled and collected , type ( 2.3 ) type (2.3) type (2.3) It can be rewritten as follows :
Q ( λ , λ ˉ ) = ∑ Y l o g ( π i 1 ) ⋅ P ( X , Y ∣ λ ˉ ) + ∑ Y [ ∑ t = 1 T − 1 l o g ( a i t i t + 1 ) ] ⋅ P ( X , Y ∣ λ ˉ ) + ∑ Y [ ∑ t = 1 T l o g ( b i t ( x t ) ) ] ⋅ P ( X , Y ∣ λ ˉ ) Q(\lambda, \bar{\lambda}) = \sum_{Y} log(\pi_{i_1}) \cdot P(X, Y | \bar{\lambda}) + \sum_{Y} [\sum_{t=1}^{T-1} log(a_{i_ti_{t+1}})] \cdot P(X, Y | \bar{\lambda}) + \sum_{Y} [\sum_{t=1}^{T} log(b_{i_t}(x_t)) ] \cdot P(X, Y | \bar{\lambda}) Q(λ,λˉ)=Y∑log(πi1)⋅P(X,Y∣λˉ)+Y∑[t=1∑T−1log(aitit+1)]⋅P(X,Y∣λˉ)+Y∑[t=1∑Tlog(bit(xt))]⋅P(X,Y∣λˉ)
therefore , Find the model parameters λ \lambda λ Maximum likelihood estimation of , It can be converted to separate calculation Maximum likelihood estimation of each parameter of the model :
π ^ i = arg max π i ∑ Y l o g ( π i 1 ) ⋅ P ( X , Y ∣ λ ˉ ) (2.4) \hat{\pi}_i = \argmax_{\pi_i} \sum_{Y} log(\pi_{i_1}) \cdot P(X, Y | \bar{\lambda}) \tag{2.4} π^i=πiargmaxY∑log(πi1)⋅P(X,Y∣λˉ)(2.4) a ^ i j = arg max π i ∑ Y [ ∑ t = 1 T − 1 l o g ( a i t i t + 1 ) ] ⋅ P ( X , Y ∣ λ ˉ ) (2.5) \hat{a}_{ij} = \argmax_{\pi_i} \sum_{Y} [\sum_{t=1}^{T-1} log(a_{i_ti_{t+1}})] \cdot P(X, Y | \bar{\lambda}) \tag{2.5} a^ij=πiargmaxY∑[t=1∑T−1log(aitit+1)]⋅P(X,Y∣λˉ)(2.5) b ^ j ( k ) = arg max π i ∑ Y [ ∑ t = 1 T l o g ( b i t ( x t ) ) ] ⋅ P ( X , Y ∣ λ ˉ ) (2.6) \hat{b}_j(k) = \argmax_{\pi_i} \sum_{Y} [\sum_{t=1}^{T} log(b_{i_t}(x_t)) ] \cdot P(X, Y | \bar{\lambda}) \tag{2.6} b^j(k)=πiargmaxY∑[t=1∑Tlog(bit(xt))]⋅P(X,Y∣λˉ)(2.6)
2.1 Initial state probability π i \pi_i πi Estimation
π ^ i = arg max π i ∑ Y l o g ( π i 1 ) ⋅ P ( X , Y ∣ λ ˉ ) (2.4) \hat{\pi}_i = \argmax_{\pi_i} \sum_{Y} log(\pi_{i_1}) \cdot P(X, Y | \bar{\lambda}) \tag{2.4} π^i=πiargmaxY∑log(πi1)⋅P(X,Y∣λˉ)(2.4) π ^ i = arg max π i ∑ i = 1 N l o g ( π i ) ⋅ P ( X , y 1 = s i ∣ λ ˉ ) (2.1.1) \hat{\pi}_i = \argmax_{\pi_i} \sum_{i=1}^{N} log(\pi_{i}) \cdot P(X, y1=s_i | \bar{\lambda}) \tag{2.1.1} π^i=πiargmaxi=1∑Nlog(πi)⋅P(X,y1=si∣λˉ)(2.1.1)
be aware π i \pi_i πi Meet the constraints ∑ i = 1 N π i = 1 \sum_{i=1}^{N} \pi_i = 1 ∑i=1Nπi=1, Write type ( 2.1.1 ) type (2.1.1) type (2.1.1) Lagrange function of :
∑ i = 1 N l o g ( π i ) ⋅ P ( X , y 1 = s i ∣ λ ˉ ) + γ ( ∑ i = 1 N π i − 1 ) (2.1.2) \sum_{i=1}^{N} log(\pi_{i}) \cdot P(X, y1=s_i | \bar{\lambda}) + \gamma(\sum_{i=1}^{N} \pi_i - 1) \tag{2.1.2} i=1∑Nlog(πi)⋅P(X,y1=si∣λˉ)+γ(i=1∑Nπi−1)(2.1.2)
Yes type ( 2.1.2 ) type (2.1.2) type (2.1.2) About π i \pi_i πi And make the result equal to 0, have to :
P ( X , y 1 = s i ∣ λ ˉ ) π i + γ = 0 \frac{P(X, y1=s_i | \bar{\lambda})}{\pi_{i}} + \gamma = 0 πiP(X,y1=si∣λˉ)+γ=0 P ( X , y 1 = s i ∣ λ ˉ ) + γ π i = 0 (2.1.3) P(X, y1=s_i | \bar{\lambda}) + \gamma \pi_{i} = 0 \tag{2.1.3} P(X,y1=si∣λˉ)+γπi=0(2.1.3)
Yes type ( 2.1.3 ) type (2.1.3) type (2.1.3) All in i i i Sum of possible situations , obtain :
∑ i = 1 N [ P ( X , y 1 = s i ∣ λ ˉ ) + γ π i ] = 0 \sum_{i=1}^{N} [P(X, y1=s_i | \bar{\lambda}) + \gamma \pi_{i}] = 0 i=1∑N[P(X,y1=si∣λˉ)+γπi]=0 ∑ i = 1 N P ( X , y 1 = s i ∣ λ ˉ ) + γ ∑ i = 1 N π i = 0 (2.1.4) \sum_{i=1}^{N} P(X, y1=s_i | \bar{\lambda}) + \gamma \sum_{i=1}^{N} \pi_{i} = 0 \tag{2.1.4} i=1∑NP(X,y1=si∣λˉ)+γi=1∑Nπi=0(2.1.4) because
{ ∑ i = 1 N P ( X , y 1 = s i ∣ λ ˉ ) = P ( X ∣ λ ˉ ) ∑ i = 1 N π i = 1 \begin{cases} \sum_{i=1}^{N} P(X, y1=s_i | \bar{\lambda}) = P(X | \bar {\lambda}) \\ \\ \sum_{i=1}^{N} \pi_{i} = 1 \end{cases} ⎩⎪⎨⎪⎧∑i=1NP(X,y1=si∣λˉ)=P(X∣λˉ)∑i=1Nπi=1 therefore
γ = − P ( X ∣ λ ˉ ) (2.1.5) \gamma = -P(X | \bar {\lambda}) \tag{2.1.5} γ=−P(X∣λˉ)(2.1.5)
So bring it into type ( 2.1.3 ) type (2.1.3) type (2.1.3) after , Get parameters π i \pi_i πi Maximum likelihood estimation of :
π ^ i = P ( X , y 1 = s i ∣ λ ˉ ) P ( X ∣ λ ˉ ) (2.1.6) \hat{\pi}_i = \frac{P(X, y1=s_i | \bar{\lambda})}{P(X | \bar {\lambda})} \tag{2.1.6} π^i=P(X∣λˉ)P(X,y1=si∣λˉ)(2.1.6)
2.2 Transfer probability a i j a_{ij} aij Estimation
a ^ i j = arg max π i ∑ Y [ ∑ t = 1 T − 1 l o g ( a i t i t + 1 ) ] ⋅ P ( X , Y ∣ λ ˉ ) (2.5) \hat{a}_{ij} = \argmax_{\pi_i} \sum_{Y} [\sum_{t=1}^{T-1} log(a_{i_ti_{t+1}})] \cdot P(X, Y | \bar{\lambda}) \tag{2.5} a^ij=πiargmaxY∑[t=1∑T−1log(aitit+1)]⋅P(X,Y∣λˉ)(2.5) a ^ i j = arg max π i ∑ i = 1 N ∑ j = 1 N ∑ t = 1 T − 1 l o g ( a i j ) ⋅ P ( X , y t = s i , y t + 1 = s j ∣ λ ˉ ) (2.2.1) \hat{a}_{ij} = \argmax_{\pi_i} \sum_{i=1}^{N} \sum_{j=1}^{N} \sum_{t=1}^{T-1} log(a_{ij}) \cdot P(X, y_t=s_i, y_{t+1}=s_j | \bar{\lambda}) \tag{2.2.1} a^ij=πiargmaxi=1∑Nj=1∑Nt=1∑T−1log(aij)⋅P(X,yt=si,yt+1=sj∣λˉ)(2.2.1)
Empathy , The application has constraints ∑ j = 1 N a i j = 1 \sum_{j=1}^{N} a_{ij} = 1 ∑j=1Naij=1 Lagrange multiplier method , We can work out a i j a_{ij} aij Maximum likelihood estimation of :
a ^ i j = ∑ t = 1 T − 1 P ( X , y t = s i , y t + 1 = s j ∣ λ ˉ ) ∑ t = 1 T − 1 P ( X , y t = s i ∣ λ ˉ ) (2.2.2) \hat{a}_{ij} = \frac{ \sum_{t=1}^{T-1} P(X, y_t=s_i, y_{t+1}=s_j | \bar{\lambda}) }{ \sum_{t=1}^{T-1} P(X, y_t=s_i | \bar{\lambda}) } \tag{2.2.2} a^ij=∑t=1T−1P(X,yt=si∣λˉ)∑t=1T−1P(X,yt=si,yt+1=sj∣λˉ)(2.2.2)
2.3 Observed probability of occurrence b j ( v l ) b_j(v_l) bj(vl) Estimation
b ^ j ( k ) = arg max π i ∑ Y [ ∑ t = 1 T l o g ( b i t ( x t ) ) ] ⋅ P ( X , Y ∣ λ ˉ ) (2.6) \hat{b}_j(k) = \argmax_{\pi_i} \sum_{Y} [\sum_{t=1}^{T} log(b_{i_t}(x_t)) ] \cdot P(X, Y | \bar{\lambda}) \tag{2.6} b^j(k)=πiargmaxY∑[t=1∑Tlog(bit(xt))]⋅P(X,Y∣λˉ)(2.6) b ^ j ( k ) = arg max π i ∑ j = 1 N [ ∑ t = 1 T l o g ( b j ( x t ) ) ] ⋅ P ( X , y t = s j ∣ λ ˉ ) (2.3.1) \hat{b}_j(k) = \argmax_{\pi_i} \sum_{j=1}^{N} [\sum_{t=1}^{T} log(b_{j}(x_t)) ] \cdot P(X, y_t=s_j | \bar{\lambda}) \tag{2.3.1} b^j(k)=πiargmaxj=1∑N[t=1∑Tlog(bj(xt))]⋅P(X,yt=sj∣λˉ)(2.3.1)
The Lagrange multiplier method is also applied , The constraint is ∑ k = 1 M b j ( k ) = 1 \sum_{k=1}^{M} b_j(k) = 1 ∑k=1Mbj(k)=1. Be careful , Only in x t = o k x_t = o_k xt=ok when b j ( x t ) b_j(x_t) bj(xt) Yes b j ( k ) b_j(k) bj(k) The partial derivative of is not always 0, Get b j ( k ) b_j(k) bj(k) Maximum likelihood estimation of :
b ^ j ( k ) = ∑ t = 1 T P ( X ∩ x ˉ t , x t = o k , y t = s j ∣ λ ˉ ) ∑ t = 1 T ∑ k = 1 M P ( X ∩ x ˉ t , x t = o k , y t = s j ∣ λ ˉ ) \hat{b}_j(k) = \frac{ \sum_{t=1}^{T} P(X \cap \bar{x}_t, x_t=o_k, y_t=s_j | \bar{\lambda}) }{ \sum_{t=1}^{T} \sum_{k=1}^{M} P(X \cap \bar{x}_t, x_t=o_k, y_t=s_j | \bar{\lambda}) } b^j(k)=∑t=1T∑k=1MP(X∩xˉt,xt=ok,yt=sj∣λˉ)∑t=1TP(X∩xˉt,xt=ok,yt=sj∣λˉ)
2.4 Baum-Welch Algorithm implementation
Input : Observation sequence of random process
Output : Maximum likelihood estimation of hidden Markov model parameters .
(1) initialization
about n = 0 n=0 n=0, Select any that meets the defined range a i j ( 0 ) , b j ( k ) ( 0 ) , π i ( 0 ) a_{ij}^{(0)}, \ b_{j}(k)^{(0)}, \ \pi_i^{(0)} aij(0), bj(k)(0), πi(0), Get the initial value of model parameters λ ( 0 ) = ( A ( 0 ) , B ( 0 ) , π ( 0 ) ) \lambda^{(0)} = (A^{(0)}, B^{(0)}, \pi^{(0)}) λ(0)=(A(0),B(0),π(0));
(2) Iterative training
a i j ( n + 1 ) = ∑ t = 1 T − 1 ξ t ( i , j ∣ X , λ ( n ) ) ∑ t = 1 T − 1 γ t ( i ∣ X , λ ( n ) ) a_{ij}^{(n+1)} = \ \frac{ \sum_{t=1}^{T-1} \xi_t(i,j | X, \lambda^{(n)}) }{ \sum_{t=1}^{T-1} \gamma_t(i | X, \lambda^{(n)}) } aij(n+1)= ∑t=1T−1γt(i∣X,λ(n))∑t=1T−1ξt(i,j∣X,λ(n))
b j ( k ) ( n + 1 ) = ∑ t = 1 , x t = o k T − 1 γ t ( j ∣ X , λ ( n ) ) ∑ t = 1 T − 1 γ t ( j ∣ X , λ ( n ) ) b_j(k)^{(n+1)} = \ \frac{ \sum_{t=1, \ x_t=o_k}^{T-1} \gamma_t(j | X, \lambda^{(n)}) }{ \sum_{t=1}^{T-1} \gamma_t(j | X, \lambda^{(n)}) } bj(k)(n+1)= ∑t=1T−1γt(j∣X,λ(n))∑t=1, xt=okT−1γt(j∣X,λ(n))
π i ( n + 1 ) = γ 1 ( i ∣ X , λ ( n ) ) \pi_i^{(n+1)} = \gamma_1(i | X, \lambda^{(n)}) πi(n+1)=γ1(i∣X,λ(n))
In style ξ t ( i , j ) \xi_t(i,j) ξt(i,j) and γ t ( i ) \gamma_t(i) γt(i) from HMM Forward algorithm and backward algorithm of the model are introduced , Please refer to the author's article for the specific derivation process : The hidden Markov model (HMM): Calculate the probability of occurrence of the observation sequence No 4 Section .
(3) End
When λ ( n + 1 ) \lambda^{(n+1)} λ(n+1) Almost no longer changes or changes are less than a given threshold ( That is, it has converged ) when , Stop iterative training . Get the maximum likelihood estimation of the model parameters :
{ a ^ i j = a i j ( n + 1 ) b ^ j ( k ) = b j ( k ) ( n + 1 ) π ^ i = π i ( n + 1 ) \begin{cases} \hat{a}_{ij} = a_{ij}^{(n+1)} \\ \\ \hat{b}_j(k) = b_j(k)^{(n+1)} \\ \\ \hat{\pi}_i = \pi_i^{(n+1)} \end{cases} ⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧a^ij=aij(n+1)b^j(k)=bj(k)(n+1)π^i=πi(n+1)
Derivation process , See the author's article :EM Algorithm (expectation maximization algorithm) Maximum likelihood estimation method of parameters of probability model with hidden variables ︎
边栏推荐
- Dataframe gets the number of words in the string
- How to restore the system of Sony laptop
- Basic usage of Frida
- What is the effect of choosing game shield safely in the game industry?
- 机器学习11-聚类,孤立点判别
- 今天14:00 | 港大、北航、耶鲁、清华、加大等15位ICLR一作讲者精彩继续!
- How to restore the system with one click on Lenovo laptop
- SystemVerilog structure (II)
- P2893 [usaco08feb] making the grade g (DP & priority queue)
- 【Try to Hack】vulnhub DC4
猜你喜欢

SQL question brushing 627 Change gender

Germany if was crowned with many awards. How strong is this pair of headphones? In depth evaluation of yinpo GTW 270 hybrid
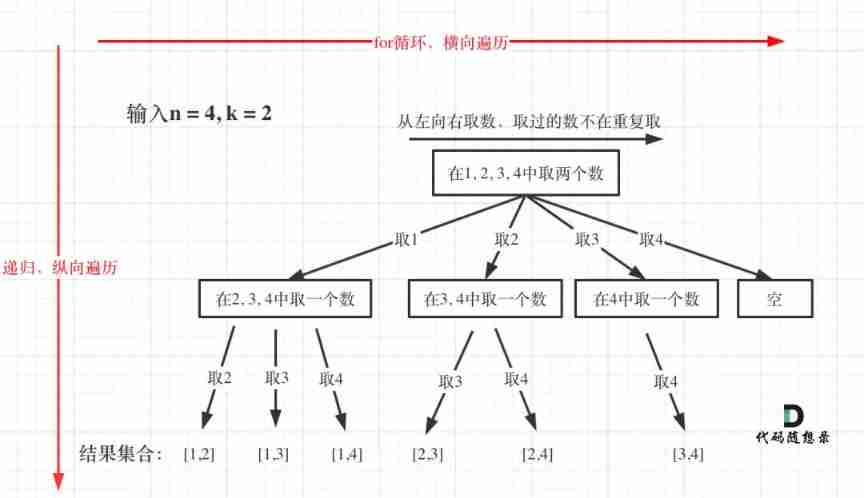
Leetcode 77 combination -- backtracking method

Tutorial on the principle and application of database system (002) -- MySQL installation and configuration: MySQL software uninstallation (Windows Environment)

Jojogan practice

数据库系统原理与应用教程(002)—— MySQL 安装与配置:MySQL 软件的卸载(windows 环境)

Ring iron pronunciation, dynamic and noiseless, strong and brilliant, magic wave hifiair Bluetooth headset evaluation

Building blocks for domestic databases, stonedb integrated real-time HTAP database is officially open source!
模板引擎Velocity 基礎
How to restore the system with one click on Lenovo laptop
随机推荐
机器学习11-聚类,孤立点判别
Is the securities account given by the head teacher of goucai school safe? Can I open an account?
China benzene hydrogenation Market Research and investment forecast report (2022 Edition)
今天14:00 | 港大、北航、耶鲁、清华、加大等15位ICLR一作讲者精彩继续!
Redis 分布式锁
Tutorial on principles and applications of database system (006) -- compiling and installing MySQL 5.7 (Linux Environment)
【C补充】【字符串】按日期排序显示一个月的日程
Soft test network engineer full truth simulation question (including answer and analysis)
How to restore the system with one click on Lenovo laptop
Why is the pkg/errors tripartite library more recommended for go language error handling?
Redis 分布式鎖
毕业季 | 华为专家亲授面试秘诀:如何拿到大厂高薪offer?
数据库系统原理与应用教程(006)—— 编译安装 MySQL5.7(Linux 环境)
How to repair the laptop that cannot connect to the wireless network
Zabbix2.2 monitoring system and application log monitoring alarm
Judge whether a binary tree is a balanced binary tree
【PyG】文档总结以及项目经验(持续更新
Is the programmer's career really short?
String class
How wild are hackers' ways of making money? CTF reverse entry Guide